CCF ADL97《图计算》整理

万物皆关联。作为表达和处理关联关系的最佳方式，图和图计算已经成为人们的关注重点和研究热点，广泛应用于金融分析、社交分析、智慧交通等诸多领域。作为大数据处理的一种典型模式，图计算不仅对计算机体系结构提出了严峻的挑战，也对系统软件、数据管理和处理模式提出了重大挑战。11.17-18有幸在武汉参加了CCF组织的ADL97《图计算》讲座，一共7位学术界和工业界的著名学者围绕大图处理的系统架构、表达存储方式，分布式计算、优化算法等方面进行了深入的讲解，两天的讲习班就像上课一样，干活满满。因为本人主要感兴趣在图挖掘算法和图应用，因此这篇博客将就讲习班的部分内容进行整理。

一、Towards Big Graph Processing: Applications, Challenges, and Advances (林学民)

1、图成为日益重要的运算对象

图结构是对群体关系的一种抽象，可以描述丰富的对象/实体和关系。图结构中，节点表示对象/实体，节点之间的边表示对象/实体之间的关系。例如：社交网络中，节点表示用户，用户之间建立的关系表示为边；学术文献中，每篇论文可以看作节点，论文的引用关系看作边；互联网上，一个个web页面代表节点，页面之间的超链接关系代表边……将现实生活中的对象/实体及其关系抽象为图数据，可以探究很多有趣的问题，如：节点权威/中心度量，社区发现，消息传播……进而指导各种应用，如利用PageRank算法计算网页权重，作为搜索排序的参考；利用最短路径算法做好友推荐；利用最小连通图识别虚假交易、洗钱等。

然后林老师重点讲解了三类图挖掘算法——子图匹配，稠密子图挖掘，图相似度计算。

2、子图匹配

定义：
给定一个查询图$q$和一个数据图$G$，找出$G$中所有与$q$同构的子图。数据图$G$可以是一个很大的图，也可以是多个中等大小的图，图中的顶点/边可以带标签也可以不带标签。子图匹配可以分为精确匹配和近似匹配，近似匹配允许一定数目没有匹配的边（mis-matched）。

应用
图分类，化合物搜索，异常检测

挑战
子图同构是一个NP难问题，搜寻结果可能非常大（MB-scale的图可以产生PB-scale的结果）。

提出的算法
①精确匹配
Tree Sequence(QuickSI)，VLDB08
Core-Forest-Leaf Decomposition(CFL Algorithm)，SIGMOD16
Optimal Join-based algorithm，VLDB15、VLDB17
②近似匹配
Spanning-tree-based matching algorithm(TreeSpan)，SIGMOD12

3、稠密子图

稠密子图是指图中相互连接比较紧密的顶点和边的集合，稠密子图通常蕴含了有趣的社会现象，对稠密子图的定义通常有如下一些指标：
k-Core： 图G的子图，其中每个节点的度都不小于k。

k-Truss： 图G的子图，其中任意一条边都被（k-2）个三角形利用。k-Truss可以看作是k-Core的加强版，k-Core只强调子图中每个顶点都至少与其他k个顶点相连，但k-Truss强调图中任意两点顶点都至少与其他k-2个顶点相连，也就是每两个顶点都至少有k-2个公共朋友。三角形是一种最简单紧密关系，图中任意两个顶点之间都有边相连，即两两都是朋友，因此这个关系很紧密。
k-Edge Connected： 图G的子图，如果删除其中任意k-1条边，其仍然是连通的。

k-Vertex Connected： 图G的子图，如果删除其中任意k-1个顶点，其仍然是连通的。
Cliques： 图G的子图，其中所有顶点两两相连。

4、图相似度计算

edit-distance： 与字符串的编辑距离类似，图的编辑是对边、节点定义编辑操作：插入、删除、替换，图$r$与图$s$的编辑距离定义为：将$r$转换成$s$所需的最小编辑操作。
SimRank： 其思想是两个顶点的入邻节点很相似，那么这两个顶点也很相似。
$$s(a,b)=\frac{C}{|I(a)||I(b)|}\sum _{i=1}^{|I(a)|}\sum _{j=1}^{|I(b)|}s(I_i(a),I_j(b))$$

其中，$I(a)$、$I(b)$分别表示顶点$a$，$b$的入邻节点。

二、Graph Computing Techniques for AI and Big Data Applications (钟叶青)

关联规则挖掘

在关联规则挖掘中涉及频繁项集计算和规则生成两个过程，频繁项集是指数据库$D$中出现频率大于支持度（support）阈值的项目集。
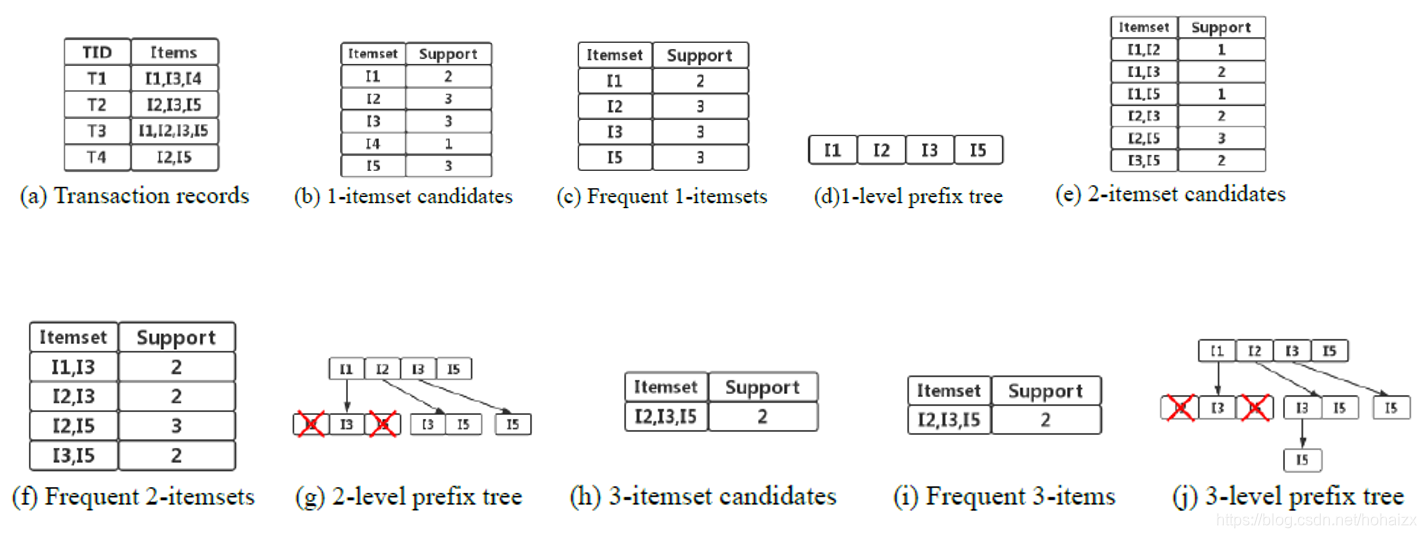
1、Apriori算法
Apriori算法是最常用的频繁项集计算算法，其思想如下：

1. 候选项集和频繁项集被存储为一棵前缀树；
2. 依据频繁k-1项集生成候选频繁k-项集；
3. 频繁k项集的子集也是频繁的；
4. 在生成候选项集后，Apriori遍历前缀树，记录每个候选项集的支持度，然后产生频繁项集。

其过程如下图：

2、基于图的方法
采用图计算的方法计算频繁项集，首先需要将数据库中的事务转换成图数据：

1. 对于每一条事务，表示为图中的顶点；
2. 如果两条事务之间有k个共同的项，那么在两条事务对应的顶点之间加入一条边，并将其属性设置为共同的k个项。

对于任意一个项集，包含该项集的顶点构成了一个连通分量，并且该连通分量中任意两个顶点之间都有一条边，因此只需要计算该连通分量包含的顶点数即可得到该项集的支持度。

当k很小时，候选项集的数目将非常的多，基于图的方法将非常耗时。而当k很大时，Apriori算法因为需要先计算所有频繁k-1项集导致性能较差，所以一个简单想法是将Apriori算法和基于图的方法结合。因此，钟老师团队提出了ANG算法—— a combination of Apriori and graph computing techniques for frequent itemsets mining。

三、Speeding Up Set Intersections in Graph Algorithms using SIMD Instructions (邹磊)

许多图算法都涉及集合求交，如：
三角形计数：

极大团

子图同构

集合求交常用思路是，首先将两个集合升序排列，然后定义两个指针，从前到后扫描两个集合，如果指针所指位置的值相等，记录该值，并同时将指针后移，如果不相等，将所指向值的指针后移。

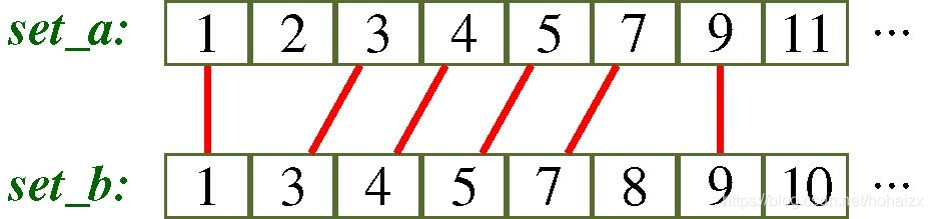
上述过程是一个复杂耗时的过程，因此目前针对集合求交都是采用的SIMD指令，SIMD：Single instruction multiple data，即一条指令处理多个数据，既一条指令能够同时并行执行在多条数据上。如下图，一条指令同时处理四条数据，能够带来4倍的加速。

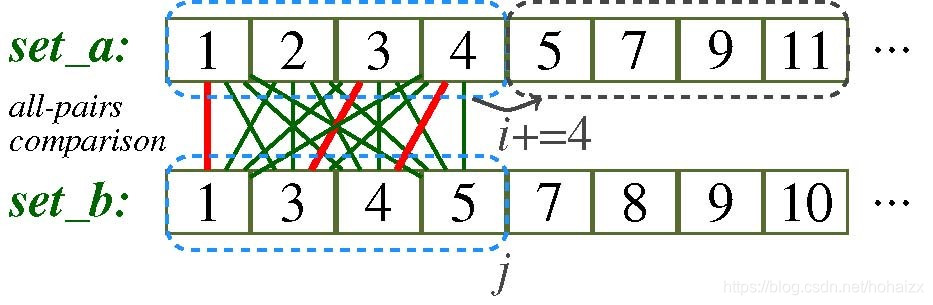
但基于SIMD带来的提速更多是依赖SIMD指令带来的硬件加速，所以可以针对集合求交算法进行优化，因此，邹磊老师团队提出Base and State Representation（BSR）

邻接列表中存储的是一个顶点的邻居节点的下标，对于图中每一个节点采用bitmap表示，每一个bit位置0/1代表该值是否出现，0代表该值没有出现，1代表该值出现过。如果一个节点的邻接节点很少，但是节点之间下标之间的间隔很大，将导致bitmap很稀疏，有很多连续为0的位置，导致两个全0的集合的无用比较。
在BSR中，将bitmap划分为大小相等的块，比如32位，然后每一块被表示成两部分，base value和state chunk，base value记录了块在bitmap中的下标，state chunk直接复制bitmap中对应位置的值，因此可以删除bitmap中全0的块。
因此，在接下来进行集合求交时首先对两个集合的base value进行比较，每次取4个base value进行匹配，过滤掉不匹配的值，然后取4个state chunk，根据base value的匹配情况进行对齐，然后比较对齐后的state chunk，得到最终结果。
在集合求交之前需要先进行节点重排序，有益于减少chunk数目。

邹磊老师定义了一个BSR压缩函数：
$$S(G,w,f,a)=\sum _{v_i\in V}{\alpha }_o(v_i)\cdot |\widetilde{N_o}(v_i)|+{\alpha }_I(v_i)\cdot |\widetilde{N_I}(v_i)|$$

四、Fast and Accurate Graph Stream Summarization (邹磊)

传统的图数据结构主要是邻接矩阵和邻接列表，邻接矩阵的空间复杂度太高$O(|V{|}^2)$，一般不用于大规模图数据的存储，因此常用邻接链表存储图数据，但邻接链表的插入/删除操作比较复杂，因而不适合流式图数据。

基本想法是：将图压缩成一个较小的图，然后采用矩阵存储。最简单的想法是采用一个哈希函数$H(\cdot )$将streaming图G映射成一个较小的图$G_h$，节点的原始ID存储在一个哈希表中，这个操作被称为图sketch。

令$M$表示映射函数的取值范围，只有$M/|V|>200$，查询正确率才会大于80%，因此存储依旧非常占用空间，为此邹磊老师提出了Graph Stream Sketch（GSS）。
Graph Stream Sketch(GSS)
图sketch $G_h$中每一条边$\overrightarrow{(H(S),H(d))}$被映射到矩阵$h(s)$行，$h(d)$列，并在该位置存储$[<f(s),f(d)>,w]$，其中address $h(v)=\lfloor H(v)/F\rfloor$，fingerprint $f(v)=H(v)$ ，对于一个16-bit的fingerprint，$F=65536$。如果矩阵中某个位置已经被占据，则将其存储到buffer中。

对于一条给定的边$\overrightarrow{(s,d)}$，首先计算出$h(s)$和$h(d)$，定位到矩阵中的对应位置，检查其中存储的值是否等于$⟨f(s),f(d)⟩$，如果是则返回边的权重，如果不相等，则检查相应的buffer。
在计算顶点$v$的1-hop后继节点时，首先定位到$h(v)$行，对于每一个$⟨f(v),f(v_s)⟩$，计算$H(v_s)=c\times F+f(v_s)$，然后查找哈希表得到原始ID。
上述想法中，buffer的存在会占据大量的内存和更新开销，但矩阵中可能还存在很多空置的bucket，可以对冲突的值进行二次哈希，填入其他空置的bucket。

总结

由于本人最近刚开始关注图计算研究，因此研究并不深入，整理总结的可能有很多不恰当的地方，欢迎大家多多指教。