本文转自acdreamer的博客
先来介绍几个与欧拉函数有关的定理:
定理一:设m与n是互素的正整数,那么
定理二:当n为奇数时,有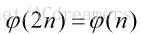
因为2n是偶数,偶数与偶数一定不互素,所以只考虑2n与小于它的奇数互素的情况,则恰好就等于n的欧拉函数值。
定理三:设p是素数,a是一个正整数,那么
关于这个定理的证明用到容斥:
由于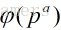
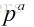


那么小于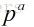


定理四:设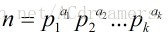
这个定理可以根据定理一和定理三证明,其实用到的就是容斥。如果对容斥熟悉,其实完全就可以直接容斥。
定理五:设n是一个正整数,那么
这个其实可以看莫比乌斯反演就明白了。
定理六:设m是正整数,(a,m)=1,则: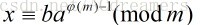

定理七:如果n大于2,那么n的欧拉函数值是偶数。
求欧拉函数值
long long Euler(long long n)
{
long long ans = n;
for (long long i = 2; i * i <= n; i++)
{
if (n % i == 0)
{
ans = ans - ans / i;
while (n % i == 0) n /= i;
}
}
if (n > 1)
ans = ans - ans / n;
return ans;
}利用递推法求欧拉函数值:
算法原理:开始令i的欧拉函数值等于它本身,如果i为偶数,可以利用定理二变为求奇数的。
若p是一个正整数满足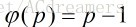
说明该数为素数。把这个数的欧拉函数值改变,同时也把能被该素因子整除的数改变。
void init()
{
for (int i = 1; i < maxn; i++) Euler[i] = i;
for (int i = 2; i < maxn; i += 2) Euler[i] >>= 1;
for (int i = 3; i < maxn; i += 2)
{
if (Euler[i] == i)
{
for (int j = i; j < maxn; j += i)
Euler[i] = Euler[i] - Euler[i] / i;
}
}
}










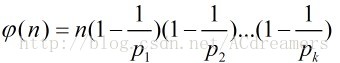
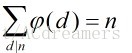














 1685
1685

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








