HDU-1426(Sudoku Killer)(dfs+巧妙思维)

最新推荐文章于 2020-02-28 19:52:51 发布
最新推荐文章于 2020-02-28 19:52:51 发布
阅读量387 收藏
点赞数
分类专栏： HDUOJ 搜索
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/hpulw/article/details/51078950
版权

HDU-1426(Sudoku Killer)(dfs+巧妙思维)

Sudoku Killer

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6079    Accepted Submission(s): 1933

Problem Description
自从2006年3月10日至11日的首届数独世界锦标赛以后，数独这项游戏越来越受到人们的喜爱和重视。
据说，在2008北京奥运会上，会将数独列为一个单独的项目进行比赛，冠军将有可能获得的一份巨大的奖品———HDU免费七日游外加lcy亲笔签名以及同hdu acm team合影留念的机会。
所以全球人民前仆后继，为了奖品日夜训练茶饭不思。当然也包括初学者linle，不过他太笨了又没有多少耐性，只能做做最最基本的数独题，不过他还是想得到那些奖品，你能帮帮他吗？你只要把答案告诉他就可以，不用教他是怎么做的。

数独游戏的规则是这样的：在一个9x9的方格中，你需要把数字1-9填写到空格当中，并且使方格的每一行和每一列中都包含1-9这九个数字。同时还要保证，空格中用粗线划分成9个3x3的方格也同时包含1-9这九个数字。比如有这样一个题，大家可以仔细观察一下，在这里面每行、每列，以及每个3x3的方格都包含1-9这九个数字。

例题：


答案：

 

Input
本题包含多组测试，每组之间由一个空行隔开。每组测试会给你一个 9*9 的矩阵，同一行相邻的两个元素用一个空格分开。其中1-9代表该位置的已经填好的数，问号（?）表示需要你填的数。
 

Output
对于每组测试，请输出它的解，同一行相邻的两个数用一个空格分开。两组解之间要一个空行。
对于每组测试数据保证它有且只有一个解。
 

Sample Input 
  
  

   
   7 1 2 ? 6 ? 3 5 8
? 6 5 2 ? 7 1 ? 4
? ? 8 5 1 3 6 7 2
9 2 4 ? 5 6 ? 3 7
5 ? 6 ? ? ? 2 4 1
1 ? 3 7 2 ? 9 ? 5
? ? 1 9 7 5 4 8 6
6 ? 7 8 3 ? 5 1 9
8 5 9 ? 4 ? ? 2 3
 

Sample Output 
  
  

   
   7 1 2 4 6 9 3 5 8
3 6 5 2 8 7 1 9 4
4 9 8 5 1 3 6 7 2
9 2 4 1 5 6 8 3 7
5 7 6 3 9 8 2 4 1
1 8 3 7 2 4 9 6 5
2 3 1 9 7 5 4 8 6
6 4 7 8 3 2 5 1 9
8 5 9 6 4 1 7 2 3
 
//注；这题的麻烦之处在于对输入数据的处理和转化。该题的判断也比较麻烦，在同一列、同一行中不能出现相同的数字。而且把大矩形分成9个小矩形，且每个小矩形中，不能出现相同的数字。

其中：大矩形分成9个小矩形，且每个小矩形中，不能出现相同的数字。这个最麻烦。

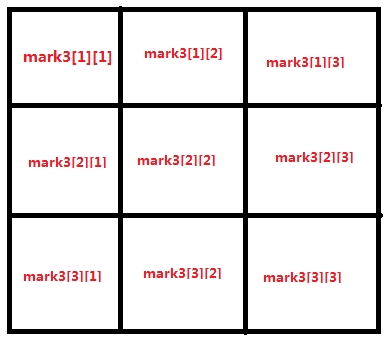
下面的代码中把大矩形分成九个小矩形，每行有3个小矩形，共有3行 。进行编号，mark3[i][j][k]数组：第i行，第j个小矩形中数字k有没有被标记 。



借助数组：c[10]={0,1,1,1,2,2,2,3,3,3}，根据当前点坐标判断当前点坐落在第几行第几列的小矩形中。

例：（i，j）

则（i，j）在第c[i]行第c[j]个小矩形中。这种方法巧妙且快速。(实际上，c[ ]数组存的是已经计算好的坐标与小矩形坐标对应的值)

之前用的是下面的多重if()判断，判断（i，j）坐落在第几行第几列的小矩形中。在初始化mark3数组以及在dfs（）判断中都需用到小矩形，因此增加了很多代码，并且非常耗时。之后用c[10]={0,1,1,1,2,2,2,3,3,3}数组就解决了这些问题。

 多重if（）判断，初始化mark3[][][]数组：

<strong><span style="font-size:18px;color:#009900;background-color: rgb(255, 255, 255);">if(i<=3)
{
	if(j<=3)
	  mark3[1][1][t]=1;
	else if(3<j&&j<=6)
	        mark3[1][2][t]=1;
		 else
		 {
		   mark3[1][3][t]=1;
	     }
}
else  if(i>3&&i<=6)
{
		if(j<=3)
		   mark3[2][1][t]=1;
		else if(3<j&&j<=6)
		   mark3[2][2][t]=1;
		else
		{
		    mark3[2][3][t]=1;
		}
}
else
{
	if(j<=3)
	   mark3[3][1][t]=1;
	else if(3<j&&j<=6)
	   mark3[3][2][t]=1;
	else
	{
	   mark3[3][3][t]=1;
	}
}</span></strong>

第一次写时，是把整个图全部遍历一遍，结果超时，且由于设置不当，在回溯过程中一组结果被输出多次。

后来看了别人的题解，改变了自己的思路。把所有的“？”点取出来，单独搜索这些点，就解决了上面的超时和结果被多次输出的问题。

My  solution：

/*2016.4.6*/

AC:

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int map[10][10],mark[10][10],mark2[10][10],mark3[4][4][10],cnt,aa,bb,c[10]={0,1,1,1,2,2,2,3,3,3};
//mark[i][k]数组：第i行中数字k有没有被标记(使用过) ，mark2[k][j]数组：第j列中数字k有没有被标记(使用过) 
//mark3[i][j][k]数组：第i行，第j个小矩形中数字k有没有被标记 。把大矩形分成9个小矩形，每行有3个小矩形，共有3行 
char cr[10];
int st;
struct stu
{
	int x,y;
}node[80];//记录？点 
void dfs(int t)
{
	int i,j,k,h,g;
	if(t==cnt)
	{
		for(i=1;i<=9;i++)
		{
			for(j=1;j<9;j++)
			printf("%d ",map[i][j]);
			printf("%d\n",map[i][9]);
		}
		return ;
	}
	i=node[t].x;
	j=node[t].y;
	for(k=1;k<=9;k++)//填充数字1~9，查看哪个符合
	{
		if(mark[i][k]==0&&mark2[j][k]==0&&mark3[c[i]][c[j]][k]==0)判断是否满足:同行、同列、同一个小矩形中数字不重复  
		{
			map[i][j]=k;//赋值 
			mark[i][k]=1;//标记 
			mark2[j][k]=1;//标记 
			mark3[c[i]][c[j]][k]=1;//标记 
			dfs(t+1);
			map[i][j]=0;
			mark[i][k]=0;
			mark2[j][k]=0;
			mark3[c[i]][c[j]][k]=0;
		}
	}
}
int main()
{
	int i,j,k,n,m,g=0,t;
     while(scanf("%s",cr)!=EOF)
	{
		if(g!=0)
		printf("\n");
		g=1;
		cnt=0;
		st=0;
		memset(mark,0,sizeof(mark));
		memset(mark2,0,sizeof(mark2));
		memset(mark3,0,sizeof(mark3));
		if(cr[0]!='?')
		{
			t=cr[0]-'0';
			map[1][1]=t;
			mark[1][t]=1;
			mark2[1][t]=1;
			mark3[1][1][t]=1;
		}
		else
		{
			node[cnt].x=1;
			node[cnt].y=1;
			map[1][1]=0;
			cnt++;
		}
		for(j=2;j<=9;j++)
		{
			scanf("%s",cr);
			if(cr[0]!='?')
			{
				t=cr[0]-'0';
				map[1][j]=t;
				mark[1][t]=1;
				mark2[j][t]=1;
				mark3[1][c[j]][t]=1;
			}
			else
			{
				node[cnt].x=1;
				node[cnt].y=j;
				map[1][j]=0;
				cnt++;
			}
		}
		for(i=2;i<=9;i++)
		for(j=1;j<=9;j++)
		{
			scanf("%s",cr);
			if(cr[0]!='?')
			{
				t=cr[0]-'0';
				map[i][j]=t;
				mark[i][t]=1;
				mark2[j][t]=1;
				mark3[c[i]][c[j]][t]=1;
		    }
			else
			{
				node[cnt].x=i;
				node[cnt].y=j;
				map[i][j]=0;
				cnt++;
			}
		}
		dfs(0);
	}
	return 0;
}


之前的代码：（如下）

/*超时，且结果输出多次：*/

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int map[10][10],mark[10][10],mark2[10][10],mark3[4][4][10],cnt,aa,bb,c[10]={0,1,1,1,2,2,2,3,3,3};
char cr[10];
int st;
void dfs(int t,int x)
{
	int i,j,k,h,g;
	if(t==(cnt+1))
	{

		for(i=1;i<=3;i++)
		{
			for(j=1;j<3;j++)
			printf("%d ",map[i][j]);
			printf("%d\n",map[i][3]);
		}
	
		return ;
	}
	for(i=x;i<=3;i++)
	{
		for(j=1;j<=3;j++)//两层for循环遍历所有点 
		{
			if(map[i][j]==0)//判断当前点是不是“？”点 
			{
				for(k=1;k<=3;k++)//填充数字1~9，判断是否符合 
				{
					if(mark[i][k]==0&&mark2[j][k]==0&&mark3[c[i]][c[j]][k]==0)//判断是否满足:同列同行同一个小矩形中数字不重复 
					{
						map[i][j]=k;
						mark[i][k]=1;
						mark2[j][k]=1;
						mark3[c[i]][c[j]][k]=1;
						dfs(t+1,i);
						map[i][j]=0;
						mark[i][k]=0;
						mark2[j][k]=0; 
						mark3[c[i]][c[j]][k]=0;
					}
				}
			}
		}
	}
}
int main()
{
	int i,j,k,n,m,g,t;
	while(scanf("%s",cr)!=EOF)
	{
		cnt=0;
		st=0;
		memset(mark,0,sizeof(mark));
		memset(mark2,0,sizeof(mark2));
		memset(mark3,0,sizeof(mark3));
		if(cr[0]!='?')
		{
			t=cr[0]-'0';
			map[1][1]=t;
			mark[1][t]=1;
			mark2[1][t]=1;
			mark3[1][1][t]=1;
		}
		else
		{
			map[1][1]=0;
			cnt++;
		}
		for(j=2;j<=3;j++)
		{
			scanf("%s",cr);
			if(cr[0]!='?')
			{
				t=cr[0]-'0';
				map[1][j]=t;
				mark[1][t]=1;
				mark2[j][t]=1;
				mark3[1][c[j]][t]=1;
			}
			else
			{
				map[1][j]=0;
				cnt++;
			}
		}
		for(i=2;i<=3;i++)
		for(j=1;j<=3;j++)
		{
			scanf("%s",cr);
			if(cr[0]!='?')
			{
				t=cr[0]-'0';
				map[i][j]=t;
				mark[i][t]=1;
				mark2[j][t]=1;
				mark3[c[i]][c[j]][t]=1;
		    }
			else
			{
				map[i][j]=0;
				cnt++;
			}
		}
		dfs(1,1);
	}
	return 0;
}


hpulw
关注
专栏目录
『杭电1426』Sudoku Killer
漠宸离若的博客
08-04 1062
Problem Description 自从2006年3月10日至11日的首届数独世界锦标赛以后，数独这项游戏越来越受到人们的喜爱和重视。 据说，在2008北京奥运会上，会将数独列为一个单独的项目进行比赛，冠军将有可能获得的一份巨大的奖品———HDU免费七日游外加lcy亲笔签名以及同hdu acm team合影留念的机会。 所以全球人民前仆后继，为了奖品日夜训练茶饭不思。当然也包括初学者linle，不过他太笨了又没有多少耐性，只能做做最最基本的数独题，不过他还是想得到那些奖品，你能帮帮他吗？你只要把答案
ZUST- 程序设计算法竞赛基础【3】
SwallowedStar的博客
04-09 390
ZUST- 程序设计算法竞赛基础【3】 1001.A strange lift 题目： Problem Description There is a strange lift.The lift can stop can at every floor as you want, and there is a number Ki(0 <= Ki <= N) on every floor.Th...
hdu 1426（数独）
yezhuyuan的博客
02-28 283
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1426 题目描述 自从2006年3月10日至11日的首届数独世界锦标赛以后，数独这项游戏越来越受到人们的喜爱和重视。 据说，在2008北京奥运会上，会将数独列为一个单独的项目进行比赛，冠军将有可能获得的一份巨大的奖品———HDU免费七日游外加lcy亲笔签名以及同hdu acm team合影留念的机会。 ...
hdu 1426
weixin_34309435的博客
09-11 113
题意：中文题，此处省。 ac代码： View Code #include<iostream> using namespace std; int map[12][12]; int k; int foat; struct tree { int i; int j; }node[90]; int check(struct tre...
HDU 1426(数独 DFS)
b338865802883204的博客
09-09 139
题意是完成数独。 记录全图，将待填位置处填 0，记录下所有的待填位置，初始化结束。在每个待填位置处尝试填入 1 - 9，若经过判断后该位置可以填入某数字，则继续向下填下一个位置， 回溯时把待填位置重新赋值为 0，总之就是深搜的思想。 要注意存数时是从 0 位置存到 8 位置，而不是从 1 位置存到 9 位置，因为这样在后面判断是否满足 3*3 的小九宫格要求时可以直接用坐标乘以 3...
hdu 1426(九宫格）
weixin_33918357的博客
04-06 93
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1426 思路：dfs搜索（回溯），有个小技巧，就是行、列的表示，具体见代码。。 View Code 1 #include&lt;iostream&gt; 2 using namespace std; 3 bool flag; 4 int map[10][10]; 5 int...
hdu 1426
bailuoheng的博客
06-07 327
题目大意： 数独游戏，往里面填1~9的数字，使每行每类和该单元格所在小3*3区域里包含1~9每个数，输出填法； 基本思路： dfs，然后就是用一个pos数组保存‘？‘的行和列，然后直接红r和c数组来表示某一行和某一列是否出现过某个数，然后这样就能在O（1）时间内判断某行某列是否成立，然后一开始不知道怎么做主要还是因为想用二重循环，但是不太会写，也不知道写出来对不对，然后就不敢写，有空一定顾上
洛谷 1784 数独（hdu 1426 Sudoku Killer）
mzj_best的博客
10-26 212
洛谷1784 数独： 首先题意是，给你一个9x9的未填满的数独（未填满用0表示），要求你将这些0的位置上填上数字，以满足数独的特性。 解析： 其实这道题爆搜就行，毕竟只是9x9的数独，直接从每个0的位置开始搜即可 上代码： #include &lt;bits/stdc++.h&gt; #define ll long long using namespace std; typedef pair&...
杭电oj 1426 Sudoku Killer(深度优先搜索 回溯）
聽竹風的博客
11-26 224
Sudoku KillerTime Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 12369 Accepted Submission(s): 3580 Problem Description 自从2006年3月10日至11日的首届数独世界锦...
HDU 1426 Sudoku Killer
surfacedust的专栏
08-14 1226
#include<stdio.h> struct node { int x,y; }p[81];//存要求的值 char ans[9][9];//存最后答案 int map[9][9],flag,num; //验证，是否符合数独条件:1 YES;2 NO; int ok(int q,int k) { int i,j,si,sj; for(i=0;i<9;i++)//验证水平&&竖直方向上是否符合 if(map[p[q].x][i]==k&&i!=p[q].y)return
HDU 1426
Leo Pan的博客
03-16 283
代码如下： #include #include #include #include using namespace std; const int MAX=10; char map_[MAX][MAX]; int pos[MAX*9][2]; bool row[MAX][MAX], list[MAX][MAX]; int k; bool check(int v,int num) {
hdu1426
Ice_Crazy的专栏
07-20 1163
/* 分析：     很有意思的一道题，DFS的，以后就不怕数独了哈哈~- -I。     我都用的scanf("%s",str)读入的，因为以前做过一道hdu的 题，说是n*n的表格，用了gets读入，最后发现是n*n的表格，不 过在给的时候，不一定是按照n*n来的 - -III。被坑怕了，就用 这个读入了。不过这个题貌似没有这种现象耶……
HDU1426 Sudoku Killer
weixin_34258782的博客
07-22 124
Sudoku Killer Time Limit: 2000/1000 MS (Java/Others)Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 3144Acc...
HDU 1426(PE多次)
youcanyouup
09-23 383
/** * hdu1426 * 遍历1-9 */#include<iostream> #include<cstdio> #include<cstring>using namespace std;const int mmax = 11; int num; int hh = 0; int map[mmax][mmax]; struct queue { int x, y; char
hdu - 1426 数独（dfs）
小冰球
11-24 223
搜索树的概念 将搜索过程中每一步的状态变成树的一个接点； 根节点为搜索树的初始状态； 搜索便是不断扩展这棵树，直至找到目标状态位置； 搜索算法的优化和改正便在于如何拓展搜索树的节点； 解题第一步：如何将状态转化为树中的结点，并构造搜索树； dfs：对于一个合法的状态A,对于其所有的子状态（搜索树的儿子结点），选择一种进行搜索，递归这一过程，直至到达叶子节点或目前状态不合法，则回溯至父亲节点，对...
HDU 1426 数独
ME4546的专栏
04-26 737
<br />http://acm.hdu.edu.cn/showproblem.php?pid=1426<br />#include<iostream> using namespace std; #define N 11 char map[N][N]; int n; bool flag; struct node { int x,y; }p[85]; void out() { for(int i=0;i<9;i++) { printf("%c",map[i][0]);
数独hdu1426
RockyHOO1209的博客
01-24 352
思路：首先输入的时候记录每一个空缺的位置，然后dfs每个空缺的位置。注意输出格式 #include #include #include #include #include #include #include #include #define inf 0x3f3f3f3f using namespace std; int sudoku[15][15]; char temp; bool v
hdu1426 数独
skyline
07-13 1881
http://acm.hdu.edu.cn/showproblem.php?pid=1426 #include #include #include #define INF 0x3f3f3f3f #define BUG printf("here!\n") using namespace std; int map[10][10]; struct node { int x,y; }; n
A - LOOPS HDU - 3853
最新发布
07-28
回答: 引用\[1\]和引用\[2\]是关于解决HDU - 3853问题的AC代码。这段代码使用了动态规划的思路，通过计算每个点的期望能量来解决问题。其中，f\[i\]\[j\]表示走到(i, j)这个点的期望能量。代码中还有一些特殊情况的...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值