将一个数组划分为和差值最小的子数组

最新推荐文章于 2021-10-10 21:04:48 发布

原创最新推荐文章于 2021-10-10 21:04:48 发布 · 2.1w 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#数组 #01背包

数据结构与算法同时被 3 个专栏收录

31 篇文章

订阅专栏

IT公司笔试面试题

15 篇文章

订阅专栏

IT名企笔试面试题

15 篇文章

订阅专栏

该博客探讨了如何将数组划分为两部分，使得两子数组的和之差最小。具体要求是数组中每个元素值在0到100之间，且元素个数在1到100之间。例如，对于数组{2, 4, 5, 6, 7}，最优解是子数组{2, 4, 6}和{5, 7}，它们的和差值为0；对于数组{2, 5, 6, 10}，最优子数组为{2, 10}和{5, 6}，和差值为1。" 114682442,10239417,Java基础教程：Arrays类详解与使用示例,"['Java基础', '数组操作', '编程技巧']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

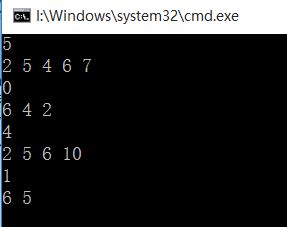
要求：将数组中的数划分为两组，使得两个子数组的和的差值最小，数组中的数的取值范围为0<X<100，元素个数也是大于0小于100.如：a[]={2,4,5,6,7},得出的两组数：{2，4，6}和{5，7}，abs(sum(a1)-sum(a1))=0;如：{2，5，6，10},abs(sum(2,10)-sum(5,6))=1所以：子数组为：{2,10}和{5,6}。

思路：很容易知道如果选取的某个子数组的和currentSum=sum/2，则这两个子数组的和的差值最小，即从数组中选取某些数字使得其和接近整个数组的1/2.，所以该命题本质上是一个01背包命题，原命题等价于从n各物品中选取若干个，其重量不超过sum/2，且重量达到最大

基于上述思路代码如下：

#include <iostream>
using namespace std;

const int M = 100;
int w[M];
int currentSum[M*M];
bool state[M][M];
int main()
{
  int n;
  while (scanf("%d ", &n) != EOF) {//输入数组元素个数
    int sum = 0;
    for (int i = 0; i < n; ++i) {
      scanf("%d", &w[i]);
      sum += w[i];//sum存储整个数组元素的和
    }
    memset(currentSum, 0, sizeof(currentSum));
    memset(state, 0, sizeof(state));
    for (int i = 0; i < n; ++i)
      for (int j = sum/2; j >= w[i]; --j) {
        if (currentSum[j] < currentSum[j-w[i]] + w[i]) {
          currentSum[j] =currentSum[j-w[i]] + w[i];
          state[i][j] = true;
        }
      }
    printf("%d\n", sum - currentSum[sum/2]*2);
    int i = n, j = sum/2;
    while (i--) {
      if (state[i][j]) {
        printf("%d ", w[i]);
        j -= w[i];
      }
    }
    printf("\n");
  }
  return 0;
}

程序运行结果如下：