Chessboard
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 14525 | Accepted: 4513 |
Description
Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below).
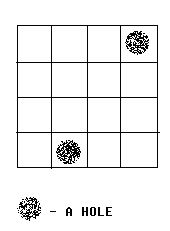
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:
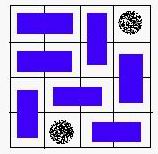
A VALID solution.
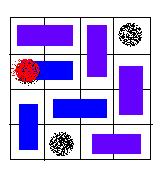
An invalid solution, because the hole of red color is covered with a card.
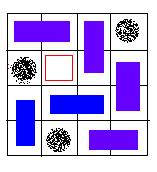
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:

A VALID solution.

An invalid solution, because the hole of red color is covered with a card.

An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.
Input
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.
Output
If the board can be covered, output "YES". Otherwise, output "NO".
Sample Input
4 3 2 2 1 3 3
Sample Output
YES
Hint
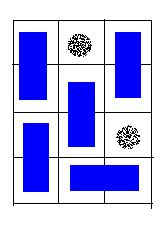
A possible solution for the sample input.
像这种n×m的棋盘图是经典的二分图,将(i+j)%2==0的点定为偶点,(i+j)%2==1的点定为奇点。一个覆盖就是一个偶点和奇点匹配。
将每个偶点与相邻的奇点连接一条边,求出二分图最大匹配数×2==n*m-k,检查是否所有的点都被匹配了。
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <stack>
#include <queue>
using namespace std;
#define maxn 1024
int dx[4]={-1,0,1,0}, dy[4]={0,1,0,-1};
vector<int> g[maxn];
void add(int u, int v)
{
g[u].push_back(v);
}
int mp[32][32];
int n,m,k;
int match[maxn];
int vis[maxn];
int dfs(int u)
{
vis[u]=1;
for(int i=0; i<g[u].size(); i++){
int v=g[u][i], m=match[v];
if(m==-1 || !vis[m]&&dfs(m)){
match[v]=u;
match[u]=v;
return 1;
}
}
return 0;
}
int hungry()
{
int res=0;
memset(match, -1, sizeof(match));
int odd=(n*m)/2;
for(int i=0; i<odd; i++){
if(match[i]<0){
memset(vis, 0, sizeof(vis));
res+=dfs(i);
}
}
return res;
}
int main()
{
while(scanf("%d%d%d", &n, &m, &k)==3){
for(int i=0; i<n*m/2; i++) g[i].clear();
int u,v;
memset(mp, 0, sizeof(mp));
for(int i=0; i<k; i++){
scanf("%d%d", &u, &v);
swap(u,v);
u--; v--;
mp[u][v]=1;
}
int odd=(n*m)/2;
for(int i=0; i<n; i++){
for(int j=0; j<m; j++)
if((i+j)%2==0 && !mp[i][j]){
u=(i*m+j)/2;
for(int d=0; d<4; d++){
int ni=i+dx[d], nj=j+dy[d];
if(mp[ni][nj]||ni<0 || nj <0 || ni>= n || nj>=m) continue;
v=odd+(ni*m+nj)/2;
add(u,v);
}
}
}
int res=hungry()*2;
if(res==n*m-k)
puts("YES");
else puts("NO");
}
return 0;
}





















 936
936











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








