1.nex数组
对于长度为 n n n的字符串 S S S,定义 n e x i = m a x { x ∣ x ∈ { 1 , 2 , . . . , i − 1 } } nex_i=max\{x|x\in \{1,2,...,i-1\}\} nexi=max{x∣x∈{1,2,...,i−1}}且 x x x满足 S 1 S 2 . . . . S x = S i − x + 1 S i − x + 2 . . . S i S_1S_2....S_x=S_{i-x+1}S_{i-x+2}...S_i S1S2....Sx=Si−x+1Si−x+2...Si。特别地,若不存在这样的 x x x,则 n e x i = 0 nex_i=0 nexi=0。
2.归纳法求解nex数组
当
i
=
1
i=1
i=1,显然有
n
e
x
1
=
0
nex_1=0
nex1=0。
当
i
>
1
i>1
i>1,设当前已经求出了
n
e
x
1
,
n
e
x
2
,
.
.
.
,
n
e
x
i
−
1
nex_1,nex_2,...,nex_{i-1}
nex1,nex2,...,nexi−1,现求解
n
e
x
i
nex_i
nexi:
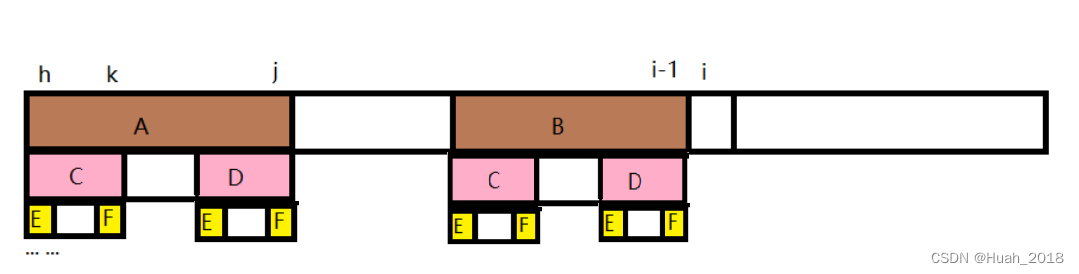
如图,不妨设
n
e
x
i
−
1
=
j
,
n
e
x
j
=
k
,
n
e
x
k
=
h
,
n
e
x
h
=
.
.
.
nex_{i-1}=j,nex_j=k,nex_k=h,nex_h=...
nexi−1=j,nexj=k,nexk=h,nexh=...
令
A
,
B
,
C
,
D
,
E
,
F
A,B,C,D,E,F
A,B,C,D,E,F为对应填充区域表示的字符串,则由
n
e
x
nex
nex数组的定义,有
A
=
B
,
C
=
D
,
E
=
F
A=B,C=D,E=F
A=B,C=D,E=F。
若
S
j
+
1
=
S
(
i
−
1
)
+
1
=
S
i
S_{j+1}=S_{(i-1)+1}=S_i
Sj+1=S(i−1)+1=Si,则
n
e
x
i
=
j
+
1
=
n
e
x
i
−
1
+
1
nex_i=j+1=nex_{i-1}+1
nexi=j+1=nexi−1+1。
证:由
A
=
B
,
S
j
+
1
=
S
i
⇒
A
+
S
j
+
1
=
B
+
S
i
A=B,S_{j+1}=S_{i}\Rightarrow A+S_{j+1}=B+S_i
A=B,Sj+1=Si⇒A+Sj+1=B+Si,再证明
j
+
1
j+1
j+1是最大的,设存在
j
+
1
<
x
<
i
j+1<x<i
j+1<x<i使得
n
e
x
i
=
x
nex_i=x
nexi=x,则有
S
1
S
2
.
.
.
S
x
−
1
S
x
=
S
i
−
x
+
1
S
i
−
x
+
2
.
.
.
S
i
−
1
S
i
⇒
S
1
S
2
.
.
.
S
x
−
1
=
S
i
−
x
+
1
S
i
−
x
+
2
.
.
.
S
i
−
1
S_1S_2...S_{x-1}S_x=S_{i-x+1}S_{i-x+2}...S_{i-1}S_i\\\Rightarrow S_1S_2...S_{x-1}=S_{i-x+1}S_{i-x+2}...S_{i-1}
S1S2...Sx−1Sx=Si−x+1Si−x+2...Si−1Si⇒S1S2...Sx−1=Si−x+1Si−x+2...Si−1从而有
n
e
x
i
−
1
=
x
−
1
>
j
nex_{i-1}=x-1>j
nexi−1=x−1>j与
n
e
x
i
=
j
nex_{i}=j
nexi=j矛盾,故
j
+
1
j+1
j+1是最大的。
若
S
j
+
1
≠
S
i
S_{j+1}\neq S_i
Sj+1=Si,则对于位置
k
k
k,若
s
k
+
1
=
S
i
s_{k+1}=S_i
sk+1=Si,则
n
e
x
i
=
k
+
1
nex_i=k+1
nexi=k+1.
证:
A
=
C
+
x
+
D
=
B
,
S
k
+
1
=
S
i
⇒
C
+
S
k
+
1
=
D
+
S
i
A=C+x+D=B,S_{k+1}=S_i\Rightarrow C+S_{k+1}=D+S_i
A=C+x+D=B,Sk+1=Si⇒C+Sk+1=D+Si,同理可证
k
+
1
k+1
k+1是最大的。
若
S
k
+
1
≠
S
i
S_{k+1}\neq S_i
Sk+1=Si,继续递归检查
n
e
x
k
,
n
e
x
n
e
x
k
,
.
.
.
nex_k,nex_{nex_k},...
nexk,nexnexk,...即可。
特别的,递归到
n
e
x
0
nex_0
nex0后则
n
e
x
i
=
0
nex_i=0
nexi=0(特别定义
n
e
x
0
=
−
1
nex_0=-1
nex0=−1)。
void kmp_next(int n,char *s)
{
//n is the length of string s
//s indexes labeled from 1 to n
nex[0]=-1;
for(int i=1;i<=n;i++)
{
int k=nex[i-1];
while(k!=-1&&s[k+1]!=s[i]) k=nex[k];
nex[i]=k+1;
}
}
3.利用nex数组进行字符串匹配
在一个字符串 T T T中查找字符串 S S S的出现次数。设有 T j − i + 1 T j − i + 2 . . . . T j = S 1 S 2 . . . S i T_{j-i+1}T_{j-i+2}....T_j=S_1S_2...S_i Tj−i+1Tj−i+2....Tj=S1S2...Si但 T j + 1 ≠ S i + 1 T_{j+1}\neq S_{i+1} Tj+1=Si+1,只需让 i i i回溯到 n e x i nex_i nexi再继续拿 S n e x i + 1 S_{nex_i+1} Snexi+1与 T j + 1 T_{j+1} Tj+1进行匹配即可,因为由 n e x nex nex数组的性质有 S 1 S 2 . . . S n e x i = S i − n e x i + 1 S i − n e x i + 2 . . . S i = T j − n e x i + 1 T j − n e x i + 2 . . . T j S_1S_2...S_{nex_i}=S_{i-nex_i+1}S_{i-nex_i+2}...S_i=T_{j-nex_i+1}T_{j-nex_i+2}...T_j S1S2...Snexi=Si−nexi+1Si−nexi+2...Si=Tj−nexi+1Tj−nexi+2...Tj。
int kmp_match(int n,int m,char *s,char *t)
{
//n is the length of string s
//s indexes labeled from 1 to n
//m is the length of string s
//t indexes labeled from 1 to m
int match_count=0;
for(int i=0,j=0;i<m;i++)
{
while(j!=-1&&s[j+1]!=t[i+1])
j=nex[j];
j++;
if(j==n)
{
match_count++;
j=nex[j];
}
}
return match_count;
}




















 683
683











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








