SVM笔记

这段时间就开始接触机器学习，看了斯坦福的公开课关于svm的内容后，觉得没怎么懂，因此想写一篇笔记，一方面梳理一下， 一方面自己以后还可以阅读。

这方面已经有一篇很棒的文章了支持向量机通俗导论大家可以去学习下

一、问题引出

最初是通过logistic回归处理一个二分类问题，对于一个样本（x[i], y[i]），x[i]是特征向量，y[i]是其分类结果（y[i]∈{0, 1}），logistic回归就是要根据输入的特征向量计算该样本分类为1的概率大小，使用的logistic公式为

• hθ(x)=g(θx)=1/（1+exp{-θx}），其中g(z)=1/(1+exp{-z})

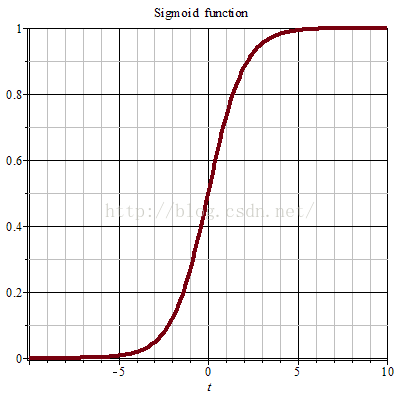
函数g(z)的功能是根据z的值将其映射到(0,1)的区间，函数图像如下（图片取自百度百科）

z的取值越大，则g(z)的值越接近1，反之z的取值越小，g(z)的取值越接近0。因此当g(z)≥0.5时可以分类y为1，g(z)<0.5时分类y为0。从函数图像可以看出，判断y为0或者1并不需要计算g(z)的具体值，只要看z是否小于0即可，更进一步的说，因为z的值越大，g(z)越接近1，也就是说y分类为1的可能性越大，反之亦然。所以为了得到一个能让我们更有信心的分类结果（大概就是这个意思，英文直译），我们希望构造一个模型，对于一个样本(x,y)，若y=1，则θx≥0且尽可能大，若y=0，则θx<0且尽可能小。

二、符号表示

对于分类的表示，从y∈{0,1}改为y∈{-1,1}，在原本的公式中，x是一个n+1维向量，n是特征数量，并将x0设置为1，而现在，x仅仅是一个n维向量，原本的θx改写为wx+b的形式，即将原本的θ0分离出来作为b。具体这些变化的原因并不是很懂，希望有高手指教下。

三、函数间隔和几何间隔

在第一点中最后，我们已经得到了模型的预期目标，即“对于一个样本(x,y)，若y=1，则θx≥0且尽可能大，若y=0，则θx<0且尽可能小”，结合起来可以得到我们的目标为

要令γ(i)尽量大，而γ(hat)=y_i*(wx_i+b)，这里的γ(i)就是函数距离。但是使用函数距离存在的一个问题是，我们可以通过任意的缩放w和b来改变最终结果的大小。因此单纯使用这样一个函数距离公式显然不合适。

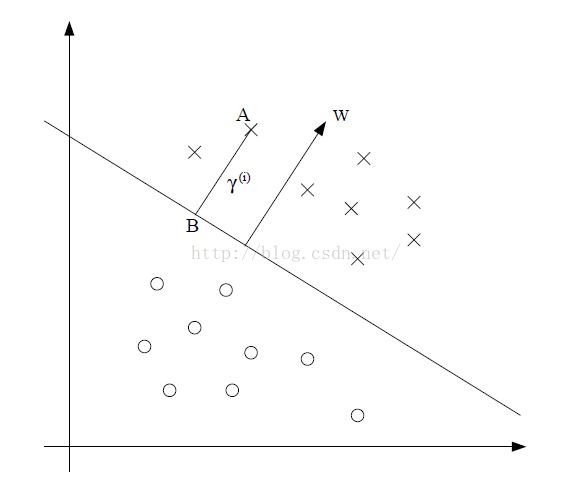
考虑如下问题（图片来源，斯坦福公开课讲义，×表示正样本，o表示负样本）：

我们的目标是找到这样一条直线wx+b=0，能够将正负样本分隔开，并且每个样本距离直线的距离尽量远。这里暂时按照在二维平面上的情况进行分析，高维情况类似，本人数学学得不好，只能就简单情况说一下。考虑点A表示的样本x(A)，其在分隔直线上的投影为点B，距离为γ_i，而w表示分隔直线的法向量，那么B点可以表示为x(B)=x(A)-γ_i（w/||w||）。因为B点落在分隔直线上，所以可以得到wx(B)+b=0，即w( x(A)-γ_i( w/||w|| ) )+b=0，根据该公式可以推出

γ_i=(w/||w||)Tx(A)+b/||w||，这里的γ_i为几何间隔（加粗的为函数间隔，不加粗的为几何间隔）。可以看出，几何间隔就是函数间隔除以w的模。

四、最优间隔分类问题

有了函数间隔和几何间隔的概念就可以对我们要求的问题进行表示，首先令γ=min γ_i,   γ=min γ_i，则要求的问题表示为

max(γ, w, b) γ，s.t. y_i(wx_i+b)≥γ，且||w||=1，i=1,2，......m

进一步可以将问题转化为

max(γ, w, b) γ/||w||，s.t. y_i(wx_i+b)≥γ，i=1,2,......,m

再进一步，通过对w和b进行缩放，使得满足γ=1，问题便可表述为

min(γ, w, b) ||w||²/2， s.t. y_i(wx_i+b)≥1，i=1,2,.....m

关于为什么要把问题进行转化，说法是因为原本的问题表示不是convex的，不易求解，至于具体convex的含义本人目前也不懂，就先不讨论了。

为了求解这个有约束的极值问题，需要用到拉格朗日乘数法，这个方法以前没听说过。。。所以看视频课时候非常困惑，这里先列出基本概念，具体求解方法等研究清楚了，再另写一篇。

五、拉格朗日乘数法

1、基本形式

拉格朗日乘数法用来求解带约束条件的极值问题，一个基本形式是

要求解 min f(w)     s.t. h_i(w)=0, i=1,2,....k

可以令F(w,β)=f(w)+∑β_i*h_i(w), i=1,2,....k

然后分别令F对w_i和β_i的偏导数为0，求解w和β。

2、一般化

更加一般化的形式是

要求解 min f(w)    s.t. g_i(w)≤0，i=1,2,.....,k

                                       且h_i(w)=0，i=1,2,.....l

需要构造L(w, α, β)=f(w)+∑{α_i*g_i(w)}+∑{β_i*h_i(w)}

观察上式可以发现，对于满足约束的w以及α_i≥0，L(w, α, β)的最大值即为f(w)，因为,g_i(w)≤0，所以α_i*g_i(w)的最大值为0（α_i≥0），而h_i(w)=0的约束使β_i*h_i(w)=0。

当这两个约束不满足时，若g_i(w)>0，那么α_i可以取任意大的值使二者乘积任意大，对于h_i(w)=0的约束也一样。

所以可以得到

约束条件满足时，max(α, β: α_i≥0)  L(w, α, β)=f(w) 

否则，                    max(α, β: α_i≥0)  L(w, α, β)=+∞

所以原始问题就变为求解min(w) max(α, β:α_i≥0) L(w, α, β)

暂时就到这里，后面的求解方法还要继续研究