uvalive 4413(梅涅劳斯定理)_梅涅劳斯定理向量-CSDN博客

本文链接：https://blog.csdn.net/hyczms/article/details/47257135

根据梅涅劳斯定理，通过给定的点坐标和边的分割比例，建立数学方程求解三角形顶点坐标。通过构建6组不同的三角形关系，推导出边长的表达式，最终解出DP并确定所有顶点位置。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

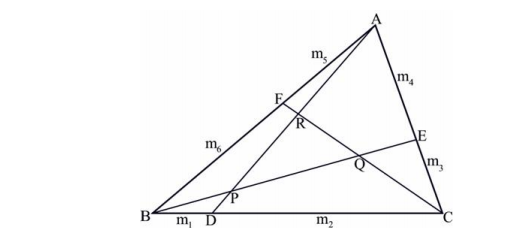
题意：如图所示，给出P、Q、R三点的坐标，AB、BC、AC被点F、D、E划分成m1:m2、m3:m4、m5:m6，给出m1~m6的数值，求△ABC的三个顶点A、B、C的坐标。
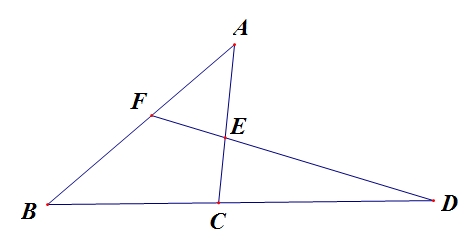
这里写图片描述

题解：根据梅涅劳斯定理，如果有两个三角形是这样组成的：
这里写图片描述

结论：(BD/DC)×(CE/EA)×(AF/FB)=1
证明省略，直接运用结论，在题中所给的三角形中有6组这样的三角形，分别可以推出后面两个边的比值：
△CBQ 和 △CDR —-> DP / CQ
△BAP 和 △BFQ —-> FR / BP
△ACR 和 △APE —-> QE / AR
△CBE 和 △CDA —-> DP / PA
△BAD 和 △BFC —-> FR / CR
△ACF 和 △AEB —-> EQ / BQ
设DP为x，就能把全部边都表示成关于x的式子，最后推回DP，就是一个关于x的一元一次方程，直接解方程就得到的DP的长度，进而所有边的长度都可以求得，为了得到A、B、C的坐标，让点R在向量PR的方向上移动AR的距离就得到了A，其余两点类似得出。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const double PI =