矩阵连乘最少次数

算法之矩阵连乘

一.问题描叙

    给定n个矩阵{A1，A2，……，An},其中Ai与Ai+1是可乘的，i=1，2，……，n-1。

   例如：

     计算三个矩阵连乘{A1，A2，A3}；维数分别为10*100 , 100*5 , 5*50

     按此顺序计算需要的次数（（A1*A2）*A3）:10X100X5+10X5X50=7500次

     按此顺序计算需要的次数（A1*（A2*A3））:10X5X50+10X100X50=75000次

     所以要解决的问题是：如何确定矩阵连乘积A1A2，……An的计算次序，使得按此计算次序计算矩阵连乘积需要的数乘次数达到最小化。

二.问题分析

   由于矩阵乘法满足结合律，所以计算矩阵连乘的连乘积可以与许多不同的计算计算次序，这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说连乘积已完全加括号，那么可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

   完全加括号的矩阵连乘积可递归地定义为：

   （1）.单个矩阵是完全加括号的；

  （2）.矩阵连乘积A是完全加括号的，则A可以表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，及A=（BC）;

    举个例子，矩阵连乘积A1A2A3A4A5，可以有5种不同的完全加括号方式：

       (A1(A2(A3A4))),(A1((A2A3)A4)),((A1A2)(A3A4)),((A1(A2A3))A4),(((A1A2)A3)A4)

    每一种完全加括号的方式对应一种矩阵连乘积的计算次序，而矩阵连乘积的计算次序与其计算量有密切的关系，即与矩阵的行和列有关。

    补充一下数学知识，矩阵A与矩阵B可乘的条件为矩阵A的列数等于矩阵B的行数，例如，若A是一个p*q的矩阵，B是一个q*r的矩阵，则其乘积C=AB是一个p*r的矩阵。

三.动态规划解决矩阵连乘积的最优计算次序问题

    或许你对动态规划有点陌生，那简单的讲讲什么叫动态规划吧。

    动态规划算法与分治法类似，其基本思想也就是将待求解的问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解，简单概括为自顶向下分解，自底向上求解。与分治法不同的是，适合于用动态规划法求解的问题，经分解得到的子问题往往不是相互独立的，换句话说，就是前面解决过的子问题，在后面的子问题中又碰到了前面解决过的子问题，子问题之间是有联系的。如果用分治法，有些同样的子问题会被重复计算几次，这样就很浪费时间了。所以动态规划是为了解决分治法的弊端而提出的，动态规划的基本思想就是，用一个表来记录所有已经解决过的子问题的答案，不管该子问题在以后是否会被用到，只要它被计算过，就将其结果填入表中，以后碰到同样的子问题，就可以从表中直接调用该子问题的答案，而不需要再计算一次。具体的动态规划的算法多种多样，但他们都具有相同的填表式。

   顺便说一下动态规划的适用场合，一般适用于解最优化问题，例如矩阵连乘问题、最长公共子序列、背包问题等等，通常动态规划的设计有4个步骤，结合矩阵连乘分析：

   （1）.找出最优解的性质，并刻画其结构特征

　　　　这是设计动态规划算法的第一步，我们可以将矩阵连乘积AiAi+1……Aj记为A[i：j]。问题就是计算A[1：n]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开，1<=k<n,使其完全加括号方式为（（A1……Ak）（AK+1……An）），这样就将原问题分解为两个子问题，，按此计算次序，计算A[1：n]的计算量就等于计算A[1：k]的计算量加上A[k+1：n]的计算量，再加上A[1：k]和A[k+1:n]相乘的计算量。计算A[1：n]的最优次序包含了计算A[1：k]和A[k+1：n]这两个子问题的最优计算次序，以此类推，将A[1：k]和A[k+1：n]递归的分解下去，求出每个子问题的最优解，子问题的最优解相乘便得到原问题的最优解。

   （2）.递归地定义最优值

           这是动态规划的第二步，对于矩阵连乘积的最优计算次序的问题，设计算A[i：j]，1<=i<=j<=n,所需要的最小数乘次数为m[i][j]，则原问题的最优值为m[1][n]。

           当i=j时，A[i：j]=Ai为单一的矩阵，则无需计算，所以m[i][j]=0，i=j=1，2，……，n。即对应的二维表对角线上的值全为0。

           当i<j时，这就需要用步骤（1）的最优子结构性质来计算m[i][j]。若计算A[i:j]的最优次序在Ak和Ak+1之间断开，i<=k<j,则m[i][j]=m[i][k]+m[k+1][j]+pi-1*pk*pj,k的位置只有j-i种可能，即k属于集合{i，i+1，……，j-1}，所以k是这j-i个位置中使计算量达到最小的那个位置。

          所以m[i][j]可以递归地定义为        m[i][j]={  0                                                            i=j

                                                                      min{m[i][k]+m[k+1][j]+pi-1*pk*pj }         i<j ,i<=k<j     }

         将对应于m[i][j]的断开位置k记为s[i][j]，在计算出最优值m[i][j]后，可递归地由s[i][j]构造出相应的最优解

   （3）.以自底向上的方式计算出最优值

          动态规划的一大好处是，在计算的过程中，将已解决的子问题答案保存起来，每个子问题只计算一次，而后面的子问题需要用到前面已经解决的子问题，就可以从表中简单差出来，从而避免了大量的重复计算

         动态规划算法 这里的p[],m[][],s[][]都为全局变量

 以A1A2A3A4A5A6为例，其中各矩阵的维数分别为：

      A1：30*35，  A2：35*15，  A3：15*5，  A4：5*10，  A5：10*20，  A6：20*25

      动态规划算法matrixchain计算m[ i ][ j ]先后次序如图所示，计算结果为m[ i ][ j ]和s[ i ][ j ]，其中第0行和第0列没有使用。

     

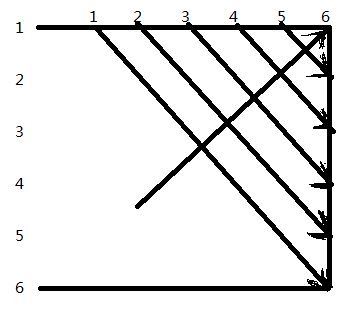
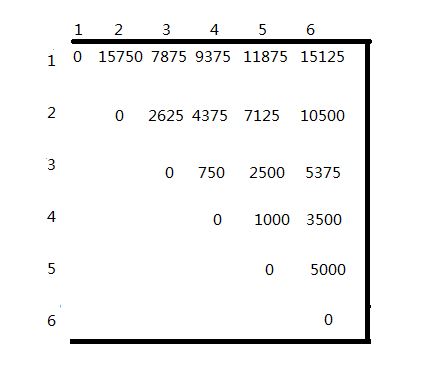
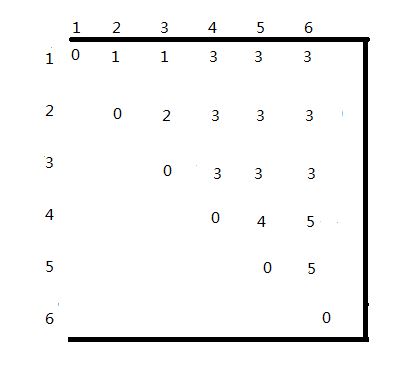
            计算次序                                                      m[i][j]                                                             s[i][j]

     

              例如，在计算m[2][5]时，依递归式有

                  

               所以m[2][5] = 7125，且k=3，因此，s[2][5]=3。

   （4）.根据计算最优值时得到的信息（及存放最优值的表格），构造最优解

         动态规划算法的第四布是构造问题的最优解。算法matrixchain只是计算出了最优值，并未给出最优解。也就是说，通过matrixchain的计算，只是到最少数乘次数，还不知道具体应按什么次序来做矩阵乘法才能达到最少的数乘次数。

****************************************************************************************************************************

模板：

#include <stdio.h>  
#include <stdlib.h>   
#define MAX 50
#define inf 99999999
int p[MAX+1];             //存储各个矩阵的列数以及第一个矩阵的行数（作为第0个矩阵的列数） 
int m[MAX][MAX];          //m[i][j]存储子问题的最优解  
int s[MAX][MAX];           //s[i][j]存储子问题的最佳分割点
int n;                    //矩阵个数
 void matrix()  
{  
   
    int i,j,k;  
    for(i=0;i<n;i++)  
        m[i][i]=0;                  //最小子问题仅含有一个矩阵 ，对角线全为0 
                               
    for(i=2;i<=n;i++)  
        for(j=0;j<n-i+1;j++)
        {                         
            m[j][j+i-1]=inf;   
            for(k=0;k<i-1;k++)
            {                                    //k代表分割点  
                if(m[j][j+i-1]>m[j][j+k]+m[j+k+1][j+i-1]+p[j]*p[j+k+1]*p[j+i])
                {  
                    m[j][j+i-1]=m[j][j+k]+m[j+k+1][j+i-1]+p[j]*p[j+k+1]*p[j+i];  
                    s[j][j+i-1]=k;                           //记录分割点  
                }  
            }  
        }  
}  
  
 void printmatrix(int leftindex,int rightindex)//递归打印输出  
{  
    if(leftindex==rightindex)  
        printf("A%d",leftindex);  
    else{  
        printf("(");  
        printmatrix(leftindex,leftindex+s[leftindex][rightindex]);  
        printmatrix(leftindex+s[leftindex][rightindex]+1,rightindex);  
        printf(")");  
    }  
}  
int main()  
{  
    int i;
    printf("请输入矩阵相乘的矩阵个数");
    scanf("%d",&n);
    printf("请依次输入矩阵的行和烈（如A*B，A=20*30，B=30*40，即输入20 30 40)\n") ;
    for(i=0;i<n+1;i++)
    {
        scanf("%d",&p[i]);
    }
    matrix();  
    printf("矩阵连乘最小次数\t%d\n",m[0][n-1]);  
    printmatrix(0,n-1);  
    printf("\n");  
    return 0;  
}