图像余弦变换

     对比度增强的一般原则都是黑的暗的还是暗的，亮的还是亮的，只不过
分的更开，简单的说就是说黑的更黑，或者白的变得更白点 。

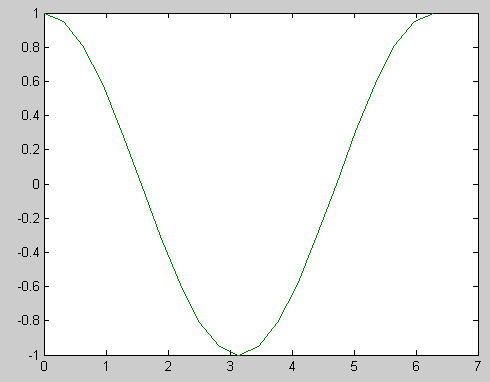
    余弦变换也可以作为一种对比度增强的方法，下面是(0,2*pi)之间的曲线，为了坚持亮的依然是亮的，暗的

还是暗的，我们可以采用(pi,2pi)即(-pi,0)，这段曲线来实现对比度增强，也可以用(pi/2,0)这段曲线来实现

对比度增强，当然也可以采用映射到(0,pi)或(0,pi/2)区间并经过变换来实现.。

    总之，变换后的曲线应当是单调递增或单调递减的，否则原本差异很大的灰度值，变换后就可能拥有相同的灰度

值。整个图像就转换错了。

 图1：余弦曲线(0,2*pi)

 

通过等式:

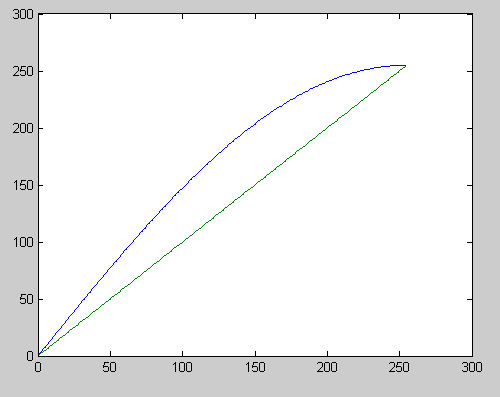
 y' = cos( pi/2*double(y)/255 -pi/2 )*255;

进行的余弦变换的效果如下图所示，图中绿线是变换前的亮度，蓝线是变换前的亮度。

从图中可以看出，整个画面的亮度都有了提升，原本

亮度为150的像素变换后亮度提升到约200.

 

图2：映射到(-pi/2)到0  空间内,

 

 

通过等式:

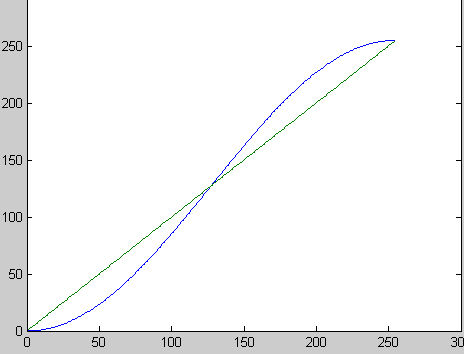
 y' = 255*(cos( pi*double(y)/255 -pi)/2 +0.5);

进行的余弦变换的效果如下图所示，图中绿线是变换前的亮度，蓝线是变换前的亮度。

从图中可以看出，图像以亮度128为中间分隔点 ，小于128时，图像变得更暗，大于

128时图像变得更亮。在实际使用过程中，可以通过一定变换将分隔点变换到其他像素值。

比如换到40，低于40的变得更暗，高于40的变得更亮。

 

 

图3:映射到空间(-pi,0),如下图所示

 

使用余弦变换能否得到较好的结果跟实际图像有关，假如原本

图像每个像素亮度都低于100，那么按图3的方式进行余弦变换只会使图像对比度减小。且图片变得更暗。

 

 

关于xiaofei26的问题的回答：

小飞26的处理方式实际上可以用表达式表示如下：

 y' =fx3 = 255* (cos( 2*pi*double(y)/255 -pi/2));  

其最终效果图如下图所表示，y'的取值既有正值也有负值，但是其通过后续处理，

根据最大值和最小值将其映射到区间(0,255)。

     为什么可以呢，因为其提供的图片非常暗，我看了一下，其绝大多数灰度值都小于60，我没发现

有大于60的(见原问题链接 

 http://topic.csdn.net/u/20080222/16/caab6ad3-a2e8-45ea-b659-bb6a5e899a55.html)，

那么从图4可以看到，这段区间内，曲线还是单调递增的，而且对

原图的亮度提升还很大，自然是可以得到比较不错的效果的。但是，如图4所示，如果换成另外一副

图片，例如图像灰度在(0,255)范围，那么这时图片就会变得混乱，因为灰度值为128的和灰度值为0的在

变换后会变成同一灰度值，其他灰度也都有这种情况。这时无论后续做什么处理，都将不能恢复原图像。

因为整个图像已经破坏了。

    那么通过余弦变换是否也可以得到好效果呢？当然可以，根据这幅图片的情况，可以将其映射到 （-pi/2,0）

的区间，一次变换不行，可以多做几次变换，我试验过，做4此变换后，效果和xiaofei26的用的方法的效果。

（无奈，原图片太暗了，当然其实还可以有其他方法，比如统计了整个像素点的亮度情况后再做余弦变换，这时

就可以把原除法的255改成除以60，这样就可以了）。具体图片见后面的图。

 

   

 

图4：

 

 

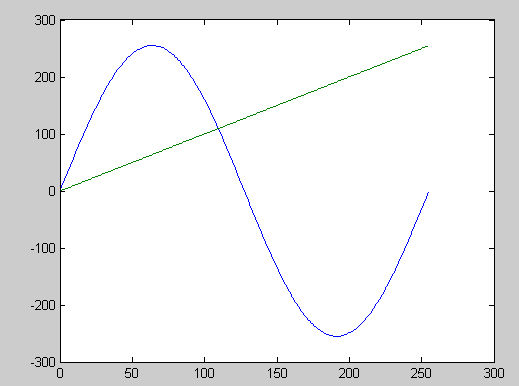
 图5：转换到区间(-pi/2,0),并将原式的/255改成 /60得到的效果图

 y' = cos( pi/2*double(y)/60 -pi/2 )*255;

 

图6：转换到区间(-pi,0),并将原式的/255改成 /60得到的效果图,(未做后续处理)

 y' = 255*(cos( pi*double(y)/60 -pi)/2 +0.5);

 

图7：转换到区间(-pi,0),并将原式的/255改成 /60得到的效果图(采用了xiaofei26提供的后续处理

即根据图片灰度的最大最小值范围进行处理)

 y' = 255*(cos( pi*double(y)/60 -pi)/2 +0.5);

 

 图8：转换到(-pi/2,0)，经过2此余弦变换得到的效果图，(未做后续处理)

 y' = cos( pi/2*double(y)/255 -pi/2 )*255;

 

 

 

 图9：转换到(-pi/2,0)，经过3次余弦变换得到的效果图，（未作后续处理）

 y' = cos( pi/2*double(y)/255 -pi/2 )*255;

 

 

 

 

 图8：转换到(-pi/2,0)，经过2次余弦变换得到的效果图，（作了后续处理）

 y' = cos( pi/2*double(y)/255 -pi/2 )*255;

 

 xiaofei26可以用下面这幅图处理一下，应该就会得到不好的图像了。