【算法】leetcode-1706 球会落何处

用一个大小为 m x n 的二维网格 grid 表示一个箱子。你有 n 颗球。箱子的顶部和底部都是开着的。

箱子中的每个单元格都有一个对角线挡板，跨过单元格的两个角，可以将球导向左侧或者右侧。

将球导向右侧的挡板跨过左上角和右下角，在网格中用 1 表示。
将球导向左侧的挡板跨过右上角和左下角，在网格中用 -1 表示。
在箱子每一列的顶端各放一颗球。每颗球都可能卡在箱子里或从底部掉出来。如果球恰好卡在两块挡板之间的 “V” 形图案，或者被一块挡导向到箱子的任意一侧边上，就会卡住。

返回一个大小为 n 的数组 answer ，其中 answer[i] 是球放在顶部的第 i 列后从底部掉出来的那一列对应的下标，如果球卡在盒子里，则返回 -1 。

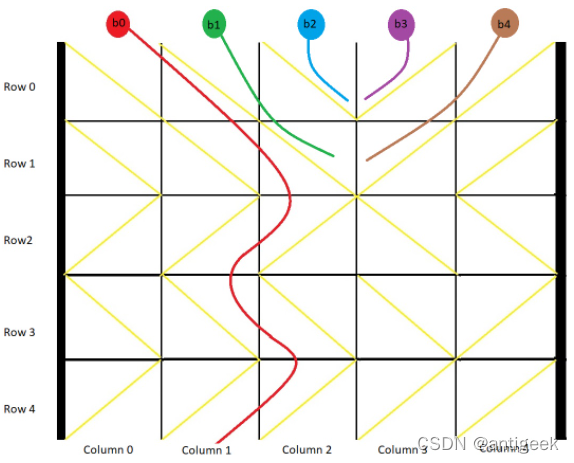
输入：grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
输出：[1,-1,-1,-1,-1]
解释：示例如图：
b0 球开始放在第 0 列上，最终从箱子底部第 1 列掉出。
b1 球开始放在第 1 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。
b2 球开始放在第 2 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b3 球开始放在第 3 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b4 球开始放在第 4 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。

class Solution {
    public int[] findBall(int[][] grid) {
        /*
          任意第r行第c列的球[r-1,c-1]，它能够继续运动的情况分为以下两种
          boll[r-1,c-1]==1,球导向右侧：c-1<列数。且 boll[r-1][c]==1
          boll[r-1,c-1]==-1,球导向左侧：c-1>0。且 boll[r-1][c-2]==-1
        */
        int columns=grid[0].length;
        int rows=grid.length;
        int[] ans = new int[columns];
        for(int c=0;c<columns;c++){
            //对于每一列，开始进行分析
            int col=c;
            ans[c]=1;
            for(int row=0;row<rows;row++){
                if(grid[row][col]==1){
                    if(col>=columns-1 || grid[row][col+1]!=1){
                        //表明该球无法继续掉落
                        ans[c]=-1;
                        break;
                    }
                    col++;
                }else{
                    if(col<=0 || grid[row][col-1]!=-1){
                        //表明该球无法继续掉落
                        ans[c]=-1;
                        break;
                    }
                    col--;
                }
                if(row==rows-1){
                    //表明最后一行的结果没有遇到break，能继续下落
                        ans[c] = col;
                }
            } 
        }
        return ans;
    }
}