考虑C(n,m)%P
情况一:n,m很大,P为素数
处理小范围的阶乘和阶乘的逆元 用卢卡斯定理即可。卢卡斯定理:
情况二: 当P=
p1∗p2∗p3∗...∗pn
求出 [Cmn] 分别在 [p1,p2,p3,…,pn] 模意义下的结果,记为 [m1,m2,m3,…,mn]
得到模方程组
xi≡mi(modpi)1≤i≤n
用中国剩余定理求解即可。
代码如下:
#include<cstdio>
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<cmath>
#define LL long long
const LL M= 999911659;
const int maxn= 50000+5;
using namespace std;
template <typename T>
inline void _read(T &x){
char ch=getchar(); bool mark=false;
for(;!isdigit(ch);ch=getchar())if(ch=='-')mark=true;
for(x=0;isdigit(ch);ch=getchar())x=x*10+ch-'0';
if(mark)x=-x;
}
LL P[4]= {2,3,4679,35617};
LL N,G,fra[maxn][4],inv[maxn][4];
LL ans[4];
LL pow_mod(LL x,LL y,LL M){
LL ans=1;
for(x%=M;y;y>>=1,x=x*x%M)
if(y&1) ans=ans*x%M;
return ans;
}
// 解模方程组 x=A[i] (moc m[i]) 0<=i<n
void EXGCD(LL A,LL B,LL& d,LL& x,LL& y){
if(B==0){d=A;x=1;y=0;}
else {EXGCD(B,A%B,d,y,x); y-= x*(A/B);}
}
LL China(LL * A,LL * m,LL n){
LL M= 1,ret=0,i;
for(i=0;i<n;i++)M*= m[i];
for(i=0;i<n;i++){
LL d,x,y,t= M/m[i];
EXGCD(m[i],t,d,x,y);
ret= (ret+ A[i]*y*t%M)%M;
}
return (ret+M)%M;
}
LL C(LL n,LL m,LL id){
if(m>n) return 0;
if(!m||n==m) return 1;
if(n<=P[id] && m<=P[id])
return fra[n][id]*inv[m][id]%P[id]*inv[n-m][id]%P[id];
return C(n/P[id],m/P[id],id)*C(n%P[id],m%P[id],id)%P[id];
}
void Divide(LL n){
LL i,j;
for(i=1;i*i<=n;i++){
if(n%i!=0) continue;
for(j=0;j<4;j++){
ans[j]= ans[j]+C(n,i,j);
if(ans[j]>=P[j]) ans[j]-=P[j];
}
if(i*i!=n){
for(j=0;j<4;j++){
ans[j]= ans[j]+ C(n,n/i,j);
if(ans[j]>=P[j]) ans[j]-=P[j];
}
}
}
}
void Init(){
LL i,j;
for(i=0;i<4;i++){ //分别预处理每一个质数
LL mod= P[i];
inv[1][i]= fra[1][i]=1;
inv[0][i]= fra[0][i]=1;
for(j=2;j<=P[i];j++){
fra[j][i]= fra[j-1][i]*j%mod;
inv[j][i]= (mod-mod/j)*inv[mod%j][i]%mod;
}
for(j=2;j<=P[i];j++) inv[j][i]= inv[j][i]*inv[j-1][i]%mod;
}
}
int main(){
cin>>N>>G;
Init();
Divide(N);
//for(int i=0;i<4;i++) cout<<ans[i]<<" ";cout<<endl;
LL exp= China(ans,P,4);
if(exp==0) exp= M-1;
cout<<pow_mod(G,exp,M)<<endl;
return 0;
}
/*
900951975 90523153
81793986
*/
终极情况:C(n,m)%p
n,m非常大 -> 卢卡斯定理
p=p1^c1 * p2^c2 * … * pn^cn
由之前的情况我们已经可以得到了一些结论,这种情况怎么办?
同理 卢卡斯定理 + CRT
但是前提条件是要求 C(n,m)% pi^ci
C(n,m)% pi^ci怎么求?
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#define ll long long
using namespace std;
const ll label=1000000000000000LL;
template <typename T>
inline void _read(T& x){
char t=getchar();bool sign=true;
while(t<'0'||t>'9'){if(t=='-')sign=false;t=getchar();}
for(x=0;t>='0'&&t<='9';t=getchar())x=x*10+t-'0';
if(!sign)x=-x;
}
ll mont(ll x,ll y,ll z){
ll temp=1;
for(x%=z;y;y>>=1,x=x*x%z){
if(y&1)temp=temp*x%z;
}
return temp;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x=1;y=0;return a;
}
else{
ll ans=exgcd(b,a%b,x,y);
ll t=x;
x=y;y=t-a/b*y;return ans;
}
}
ll rev(ll a,ll b){
ll x,y;
exgcd(a,b,x,y);
return (x%b+b)%b;
}
ll C(ll n,ll m,ll mod){
if(m>n)return 0;
ll ans=1,i,a,b;
for(i=1;i<=m;i++){
a=(n+1-i)%mod;
b=rev(i%mod,mod);
ans=ans*a%mod*b%mod;
}
return ans;
}
ll C1(ll n,ll m,ll mod){
if(m==0)return 1;
return C(n%mod,m%mod,mod)*C1(n/mod,m/mod,mod)%mod;
}
ll cal(ll n,ll p,ll t){
if(!n)return 1;
ll x=mont(p,t,label),i,y=n/x,temp=1;
for(i=1;i<=x;i++){
if(i%p)temp=temp*i%x;
}
ll ans=mont(temp,y,x);
for(i=y*x+1;i<=n;i++){
if(i%p)ans=ans*i%x;
}
return ans*cal(n/p,p,t)%x;
}
ll C2(ll n,ll m,ll p,ll t){
ll x=mont(p,t,label);
ll a,b,c,ap=0,bp=0,cp=0,temp;
for(temp=n;temp;temp/=p)ap+=temp/p;
for(temp=m;temp;temp/=p)bp+=temp/p;
for(temp=n-m;temp;temp/=p)cp+=temp/p;
ap=ap-bp-cp;
ll ans=mont(p,ap,x);
a=cal(n,p,t);
b=cal(m,p,t);
c=cal(n-m,p,t);
ans=ans*a%x*rev(b,x)%x*rev(c,x)%x;
return ans;
}
ll CRT(ll A[],ll B[],ll r){
ll M=1;
ll i,j,k,ans=0,d,t,x0,y0;
for(i=1;i<=r;i++){
M*=A[i];
}
for(i=1;i<=r;i++){
d=M/A[i];
exgcd(d,A[i],x0,y0);
ans=(ans+d*x0*B[i])%M;
}
while(ans<=0)ans+=M;
return ans;
}
ll lucas(ll x,ll y,ll mod){
ll i,j,k,d,cnt=0,t;
ll A[205],M[205];
for(i=2;i*i<=mod;i++){
if(mod%i==0){
t=0;
while(mod%i==0){
mod/=i;
t++;
}
M[++cnt]=mont(i,t,label);
if(t==1)A[cnt]=C1(x,y,i);
else A[cnt]=C2(x,y,i,t);
}
}
if(mod>1){
M[++cnt]=mod;
A[cnt]=C1(x,y,mod);
}
/*cout<<"divide:"<<endl;
for(i=1;i<=cnt;i++){
cout<<"M:"<<M[i]<<" residue:"<<A[i]<<endl;
}*/
return CRT(M,A,cnt);
}
int T;
int main(){
ll x,y,temp;
cin>>T;
while(T--){
scanf("%I64d%I64d%I64d",&x,&y,&temp);
printf("%I64d\n",lucas(x,y,temp));
}
}
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
const ll label=1000000000000000LL;
template <typename T>
inline void _read(T& x){
char t=getchar();bool sign=true;
while(t<'0'||t>'9'){if(t=='-')sign=false;t=getchar();}
for(x=0;t>='0'&&t<='9';t=getchar())x=x*10+t-'0';
if(!sign)x=-x;
}
int T;
ll mod;
ll cnt;
ll n,m,n1,n2,c;
ll a[25];
ll A[205],M[205],prime[205],index[205];
ll F[50005];
ll mont(ll x,ll y,ll z){
ll temp=1;
for(x%=z;y;y>>=1,x=1ll*x*x%z){
if(y&1)temp=1ll*temp*x%z;
}
return temp;
}
void pre(){
ll MOD=mod,i,t;
for(i=2;i*i<=MOD;i++){
if(MOD%i==0){
t=0;
prime[++cnt]=i;
while(MOD%i==0){
MOD/=i;
t++;
}
M[cnt]=mont(i,t,label);
index[cnt]=t;
}
}
if(MOD>1){
M[++cnt]=MOD;
prime[cnt]=MOD;
index[cnt]=1;
}
}
ll exgcd(ll a,ll b,ll &x,ll &y){
if(b==0){
x=1;y=0;return a;
}
else{
ll ans=exgcd(b,a%b,x,y);
ll t=x;
x=y;y=t-a/b*y;return ans;
}
}
ll _fac(ll n,ll t){
if(n<prime[t])return F[n];
c+=n/prime[t];
return 1ll*mont(F[M[t]-1],n/M[t],M[t])*F[n%M[t]]%M[t]*_fac(n/prime[t],t)%M[t];
}
ll C(ll n,ll m,ll t){
if(n<m)return 0;
if(m<0)return 0;
if(n==m)return 1;
ll i,p,temp,x,y,s;
F[0]=1;
for(i=1;i<M[t];i++){
if(i%prime[t])F[i]=F[i-1]*i%M[t];
else F[i]=F[i-1];
}
c=0;
p=_fac(n,t);
s=c;c=0;
temp=1ll*_fac(m,t)*_fac(n-m,t)%M[t];
exgcd(temp,M[t],x,y);
x=(x+M[t])%M[t];
p=1ll*p*x%M[t]*mont(prime[t],s-c,M[t])%M[t];
return p;
}
ll lucas(ll n,ll m){
if(n<m||m<0)return 0;
if(n==m)return 1;
//cout<<"lucas("<<n<<","<<m<<")"<<endl;
ll temp=0,x,y,i,t;
for(i=1;i<=cnt;i++){
//cout<<"i:"<<i<<" prime:"<<prime[i]<<" mod:"<<M[i]<<" index:"<<index[i]<<endl;
t=mod/M[i];
exgcd(t,M[i],x,y);x=(x+M[i])%M[i];
temp=(temp+1ll*x*C(n,m,i)%mod*t%mod)%mod;
}
return temp;
}
int main(){
ll i,j,k;
cin>>mod;
pre();
}








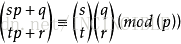














 282
282











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








