计算机逻辑

最新推荐文章于 2025-03-15 22:08:06 发布

init33

最新推荐文章于 2025-03-15 22:08:06 发布

阅读量1k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：计算机基础文章标签：硬件电脑硬件

本文链接：https://blog.csdn.net/init33/article/details/121254049

计算机基础专栏收录该内容

3 篇文章

订阅专栏

本文详细介绍了计算机硬件中的信息表示，包括数制、数码、数据的定点与浮点表示，以及字符型数据的ASCII码和汉字码。此外，还探讨了逻辑代数的基础运算、描述方法及函数式化简。内容涵盖二进制、真值、原码、补码、浮点数格式（如IEEE754）以及逻辑运算的基本概念。

硬件结构——信息表示

前言

前言

本篇采用自下而上的方式分析计算机硬件基本逻辑

一.信息表示

数字信号是信息的载体，数字电路中数字信号以数码的形式表示。数码表示数量大小时，可以进行算术运算，同时多位数码中每一位的构成方法和从低位到高位的进制规则为数制。数码表示不同事物或相同事物的不同状态时，数码可称为代码，代码的规则称为码制，如ASCII码。

1.数制

数制的基本属性
基：数制每一位上允许使用的数码个数称为”基”。
权：某数制每一位所具有的值称为”权”。
进制是指进位计数制，一位数码等于或超过基数时就要进位。
基于数制的基本属性就能实现任意数制间的转换

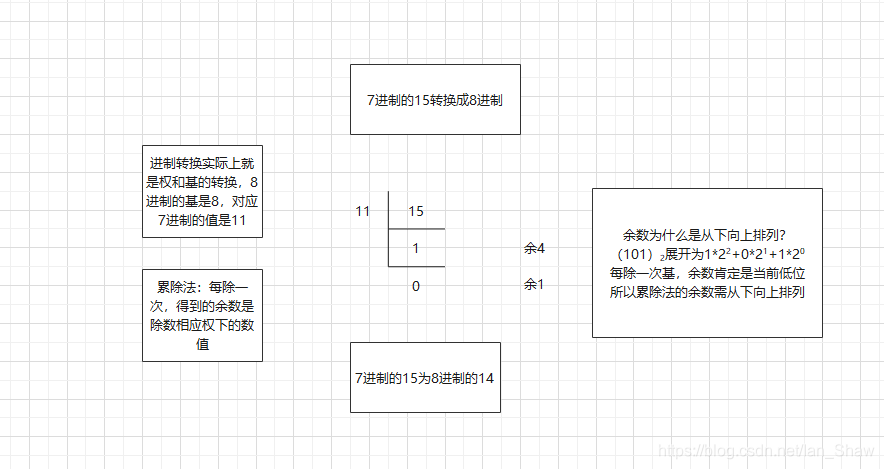
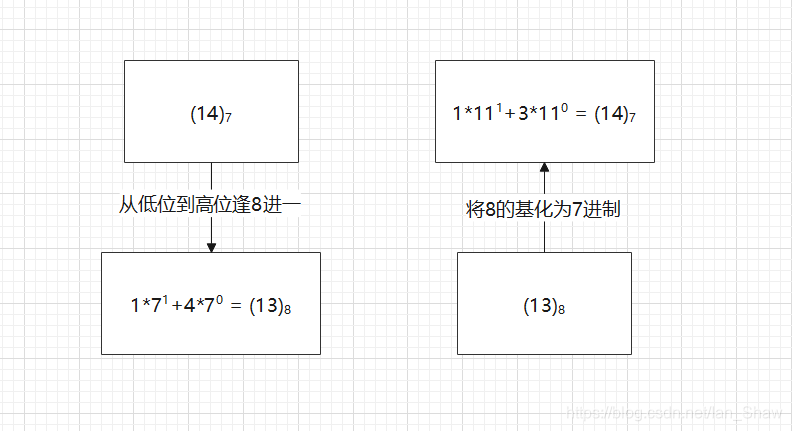
在这里插入图片描述

取余法

在这里插入图片描述

取整法

在这里插入图片描述

2.数码

数字电路使用二值逻辑，主要是二进制数码

真值
计算机数值表示中，用正负号加绝对值表示数据的形式被称为“真值”。
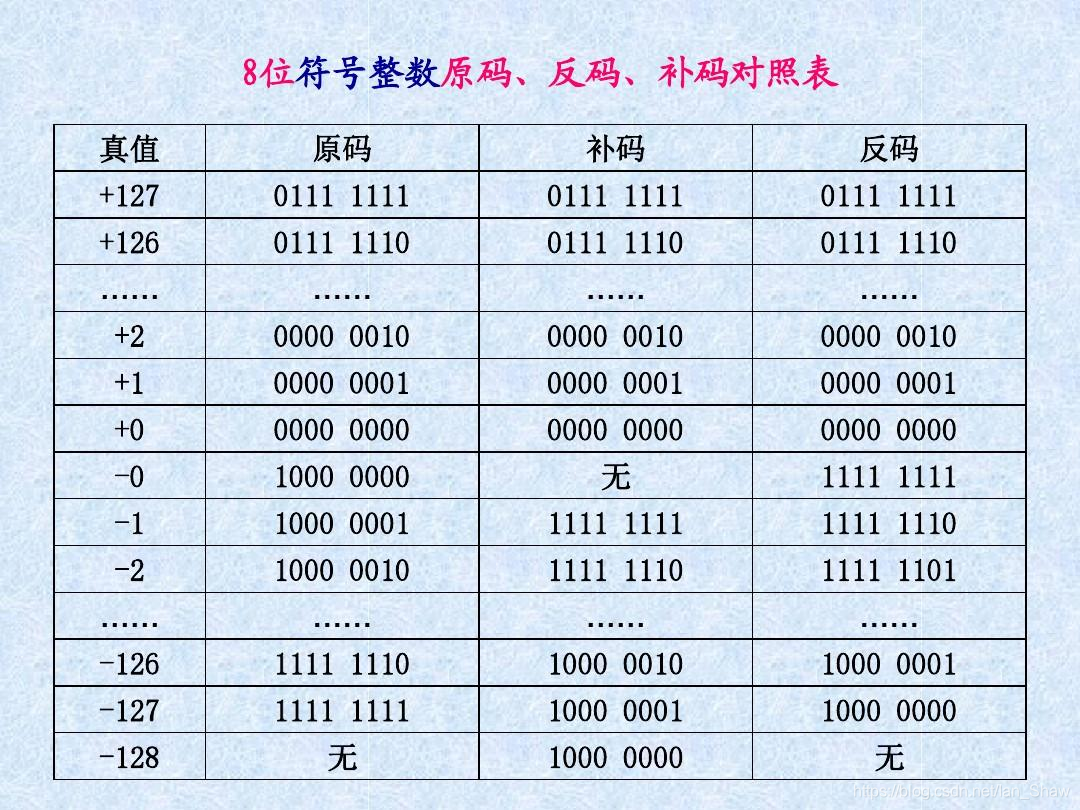
原码
相对于真值，符号位用数码表示，数值位不变
反码
原码除符号位外按位取反，原码求补码的过渡码
补码
真值加2ⁿ（n为总位数）即补码。但是单符号位的补码存在算术溢出问题
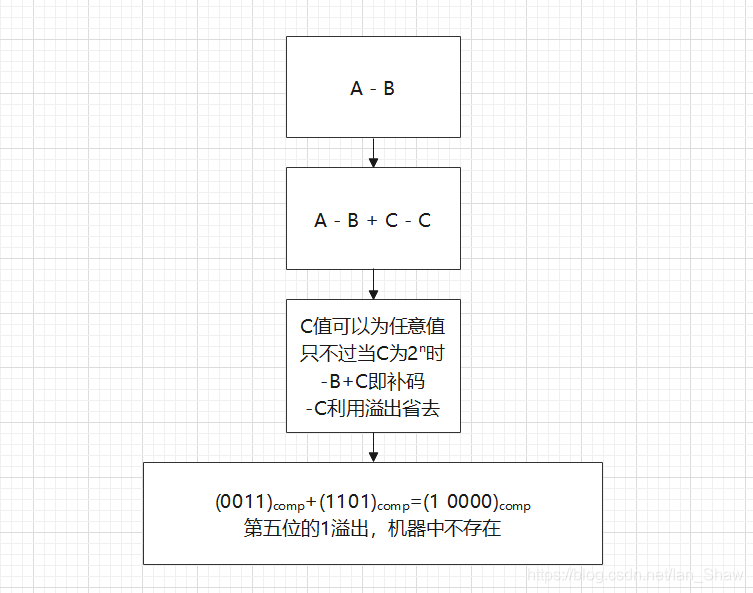
在这里插入图片描述

在这里插入图片描述

补码的‘0’只有一种形式

移码
将二进制真值正向平移或加上2^n-1（n为总位数），即全部转换成无符号数，通常表示阶码，便于比较大小

3.数据

定点数
数的小数点固定不变(数值位为n)
1、带符号的定点小数：约定所有数的小数点在符号位后，范围-（1-2^-n）~1-2^-n，通常是原码或补码
2、带符号的定点整数：约定所有数的小数点在最低位后，范围-2^n-1~2^n-1，通常是原码或补码
3、无符号的定点整数：范围0~2ⁿ⁺¹-1，通常是移码
在这里插入图片描述
浮点数
小数点的位置可以按需浮动，相同字长较定点数表示范围更大、精度更高

通用格式：阶符+阶码+数符+尾数
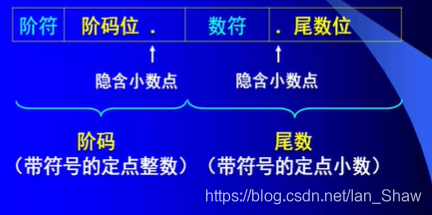
在这里插入图片描述
规格化格式：固定尾数，使浮点数表示代码唯一。阶码的精度为1，所以限制尾数在1个偏移内。
原码表示时：1/2 =< |M| < 1 （范围不包括-1、+1）
补码表示时：-1 =< M < -1/2 1/2 =< M < 1 （范围不包括-1/2、+1）
在这里插入图片描述

IEEE754标准：阶码用移码表示
float 的阶码8位数符1位尾数 23位，并且尾数隐含为1.x，所以范围约3.4e³⁸= 2¹²⁸ ，同时23位尾数可以表示的10进制数最大为16,777,216，所以有效位7~8位
double 的阶码11位数符1位尾数 52位，所以范围约1.7e³⁰⁸= 2¹⁰²⁴，同时52位尾数可以表示的10进制数最大为9,007,199,254,740,992，所以有效位15~16位
在这里插入图片描述
字符型数据
ASCII码：7位有效位+1位奇偶校验位。所以共可以表示128个字符，包括字母、数字、运算符、标点符号、标示符、格式控制符。奇偶校验位是用来简单检测数据传输中是否存在错误，例如，校验位为奇校验位时，当数据有效位中1的个数为奇数时，校验位为1，传输过程中有效位中1的个数变成了偶数，则可通过校验位判断传输发生错误。
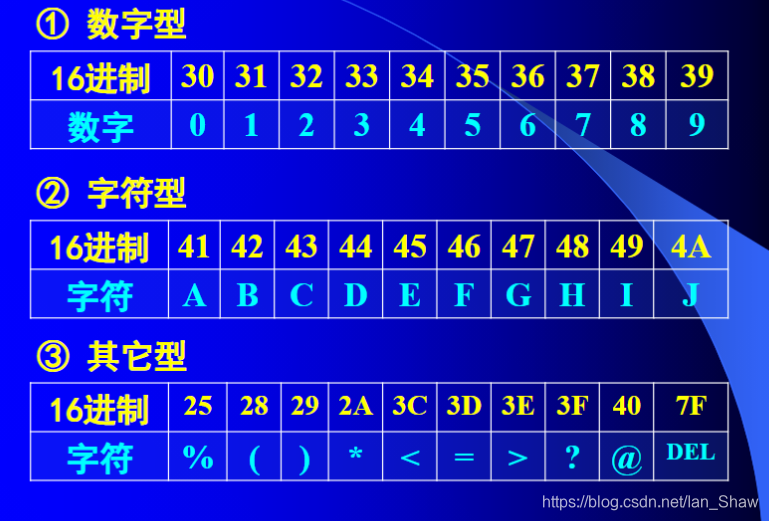
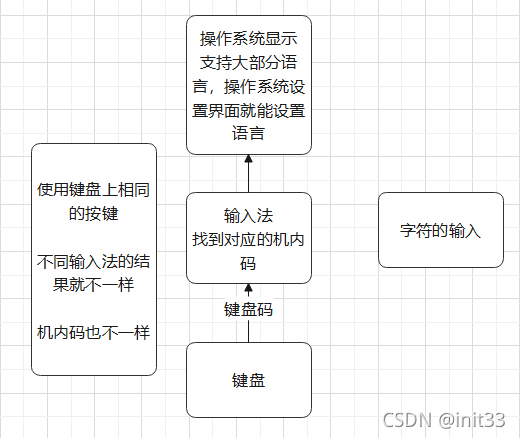
在这里插入图片描述
汉字码¹
输入码：数字码（区位码）、拼音码（拼音输入法）、字形码（五笔输入法）
内码：国标码（通常转换成机内码存储，以和ASCII码区分）、GBK、Unicode
输出码：字模码（将内码转换成点阵，以实现各种字体）
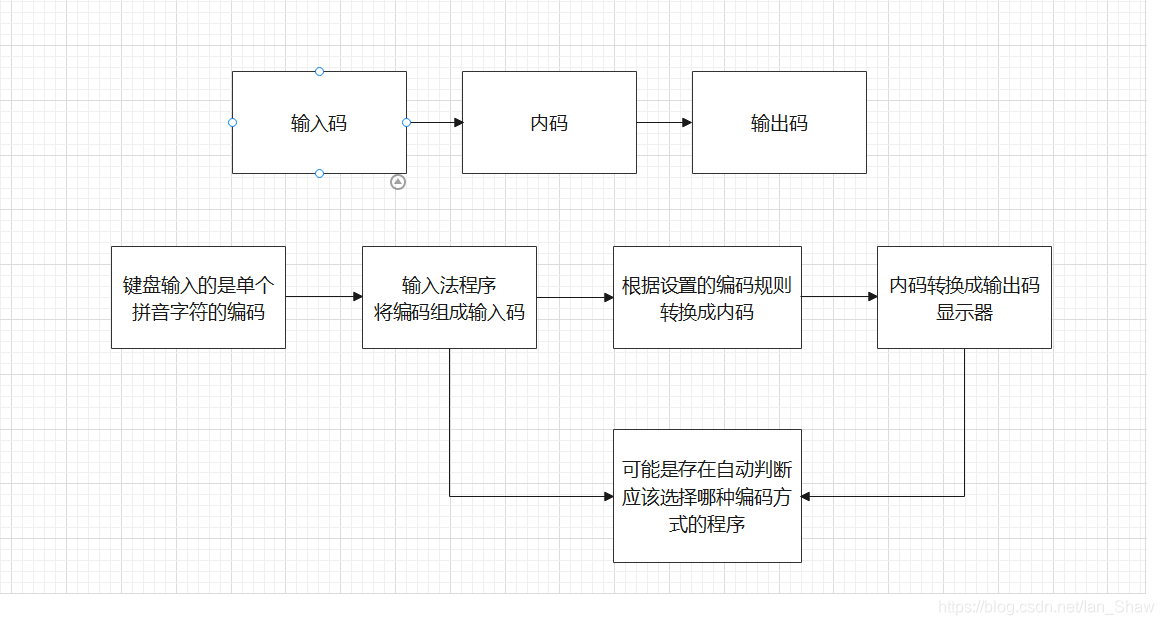
在这里插入图片描述
字符的显示

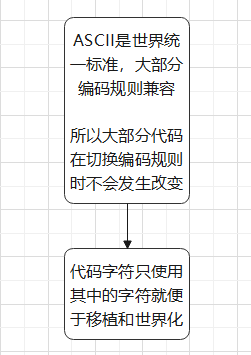
#include<bits/stdc++.h>
using namespace std;
int main(int argc,char *argv[]){
    printf("是");
    return 0;		//使用GB2312编码，输出 是
}

#include<bits/stdc++.h>
using namespace std;

int main(int argc,char *argv[]){
    printf("��");
    return 0;		//相同的代码转换成UTF-8编码，显示变成乱码，输出正确 是
}

在这里插入图片描述

4.基本操作

移位：逻辑移位（循环左移最高位会移动至最低位）、算术移位（相当于乘除2、负数补码移位时在空位补1、如果是双符号位第二符号位要参与移动）
舍入：末位恒置1、0舍1入
扩展：符号位扩展（符号位为0高位补0，符号位为1高位补1）、0扩展（高位补0，用于无符号数）
压缩：弃高位留低位
存储：小端模式（小地址单元存储数据低位）、大端模式（大地址单元存储数据低位）
字的对齐：按边界对齐（按字存储，读取次数少）、不按边界对齐（按字节存储，存储利用率高）

二.逻辑代数

分析数字电路逻辑功能的数学方法

2.1.基本运算

基本运算包括与、或、非

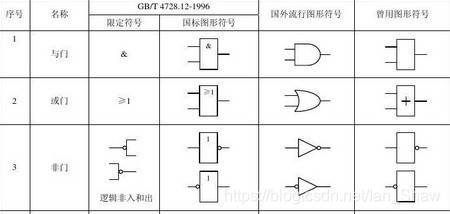
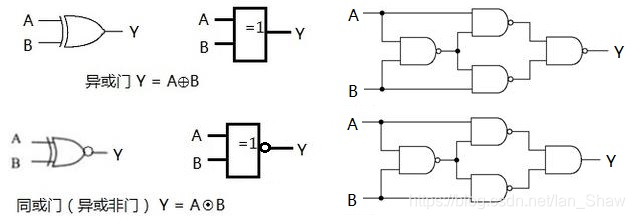
在这里插入图片描述

2.2.描述方法

包括逻辑真值表、逻辑函数式、逻辑图、波形图

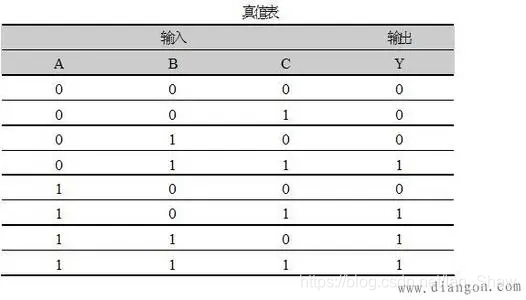
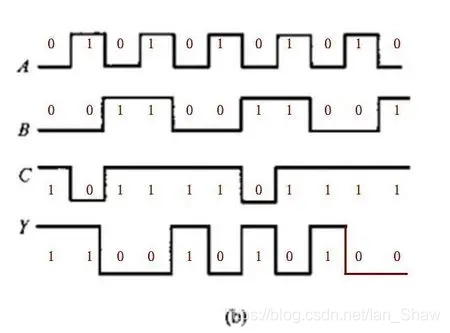
在这里插入图片描述

2.3.逻辑函数式化简方法

2.3.1.标准形式

值为1的最小项之和或值为0的最大项之积。

最小项性质
性质是由定义确定的

对于任意一个输入变量有且只有一个最小项为1。
具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
对于输入变量的任何一组取值，任意两个最小项的乘积为0。
对于输入变量的任何一组取值，全体最小项的和为1。
最小项通常用m表示，下标i即最小项编号，将最小项中的原变量用1表示，非变量用0表示，得到的二进制编码转换成十进制，可得到最小项的编号。

2.3.1.化简方法

通用卡诺图化简，原理是利用了最小项或最大项的逻辑相邻性.
若存在约束项或任意项可以充当1或0使用.
若对象是多输出逻辑函数则可寻找卡诺图中不同输出间的相同项.

步骤

函数化为最小项之和
画出卡诺图
找出可合并最小项
选取化简后的乘积项：覆盖所有最小项、乘积项最少、乘积项包含的因子最少

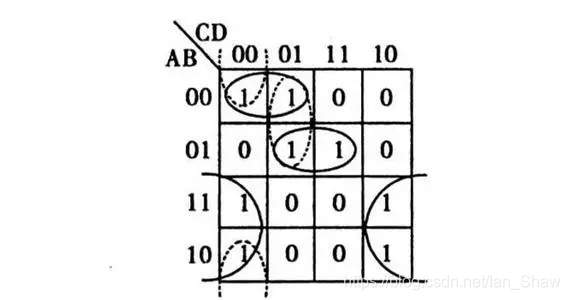
在这里插入图片描述

以上纯属个人观点，欢迎大佬批评指正（待填坑）

https://www.icourse163.org/learn/UESTC-1001543002?tid=1463003450#/learn/content?type=detail&id=1240111317&cid=1261430013 ↩︎