蚂蚁爬橡皮筋问题

         关于这个问题很多地方都有讨论。例如 http://blog.csdn.net/kofsky/article/details/2863590 还有 http://blog.csdn.net/born1985man/article/details/4676422 这里写点不一样的理解与解法。

        原题为 “一条可以均匀拉伸无限拉伸的橡皮筋，初始长度为1米，一个累不死的蚂蚁，从橡皮筋的一端爬到另一端，蚂蚁爬行速度为1厘米每秒，橡皮筋拉伸的速度为10厘米每秒！问：蚂蚁可以爬到橡皮的另一端吗？如果可以要用多久的时间！”

       为讨论方便起见，橡皮筋初始长度用L0表示，蚂蚁爬行速度用Va表示，橡皮筋拉伸速度用Vr表示。      

       首先要明白一件事，橡皮筋拉伸速度应该是相对地面而言的。其次这里说的Va的参照系应该是针对橡皮筋而言的，因为蚂蚁就是在橡皮筋上爬的。假设是相对地面。那么这只蚂蚁累到死，也是不可能到达另一端的。那么我们只需要把蚂蚁的速度转换为相对地面参考系的速度，问题就比较容易解答了。

 

       速度合成式为     蚂蚁相对地面速度 = Va + 当前蚂蚁所在位置的伸长速度

 

       再多几个假设。假设橡皮筋两端分别为a与b,  a 左, b右。a点固定，b点被拉伸。在拉伸开始时设a 点往右 x 处有一点c。那么不管经过多长时间。 c所处位置在橡皮筋的长度中所占的比例不变.

                          

                                                        
                                      

                    c点的拉伸速度为 :    

                           

 

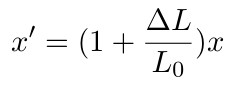
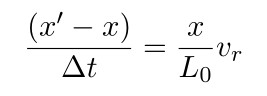
          注意这个速度会一直保持不变,而且只和它在橡皮筋中所占的比例相关。所以如果经过 t 时间，橡皮筋上距离 a 点 s 处的速度应该为

                                    
                                 
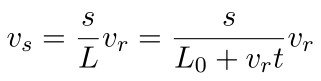
         所以合成速度为:

                               

 

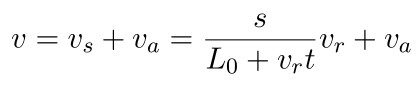
               再应用速度与位移的微分方程:

                          就得到
                                 
 
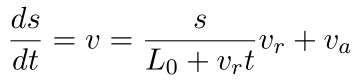
                  再解这个一阶线性非齐次微分方程

                 

                  可得

                        

 

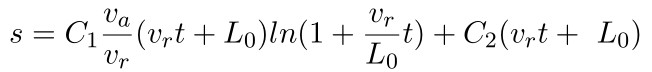
                            把 t = 0 时 s = 0代入，求得 C2 = 0;

                            则

 
                         
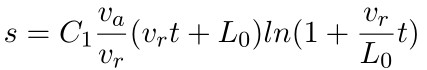
                     再求得

 
                      

 

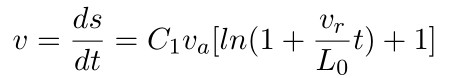
                           同样地，根据题意t = 0时，v = Va, 又得C1 = 1

 

                           所以：

                           
                          

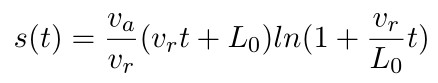
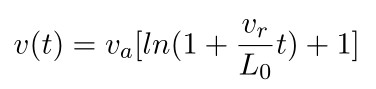
                   更好的思路推荐

http://blog.csdn.net/kofsky/article/details/2864842 写道

续：直接积分，按蚂蚁爬行距离占橡皮筋比例来讨论

假设经过时间t后，蚂蚁到达位置s，此时橡皮筋长度为L=l+v2t。由时间t经过时间dt后，蚂蚁爬行的距离为v1dt，由于时间短很小，因此可假定橡皮筋还来不及拉伸，在这段极短的时间dt内，蚂蚁爬行的距离占整个橡皮长度的比例为

     注意他的速度合成公式是错的  不应该是 V = Va - (1 - r) Vr , 而应该是 V = Va + r * Vr 。这个速度合成公式和我们的是一致的。