在C/C++中,有以下基本类型
bool 表示真假
char 表示了256个字符
以下三个类型,表示scalar numbers(任意标量值)
short(2 bytes),int(4 bytes),long(4 bytes)
以下两种类型,表示arbitrarily precise numbers(任意精度值),用它们所表示的字节数尽可能的表示任意精度值。
float 4 bytes
double 8 bytes
binary digit ---> bit
8个比特代表一个字节,我们可以用下图来形象的表示,

每一个比特位进行0、1选择,每一位都相对独立。
其正好是char类型的大小,故char类型可以表示2的八次方(256)个字符,所以ASCII表非常大。
以'A' 为例,在计算机中,必须将其想象成一个特定的数字,其ASCII码值为65, 故观察内存时,其比特位表示为0100 0001 。
用short类型表示数字时,如下

对应为2^9 + 2^2 + 2^1 + 2^0 = 519
当short类型表示如下数时,

对应为2^15 - 1
最高比特位对于数字的表示的大小并无影响,它只表示数字的正负,0表示正数,1表示负数。如下图

我们直观意义上认为以上二者相加时,只需将比特位相加即可得到0,而事实上若如此做,我们将会得到

因此,在正负数相加时,如何才能够将所有位数清零呢?
以7为例
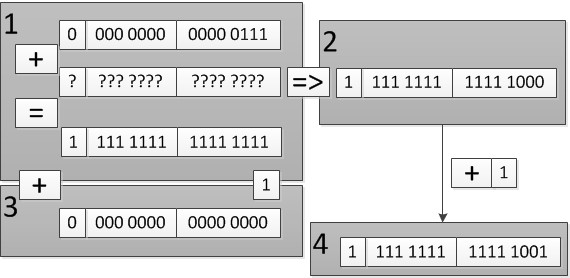
在上图的1状态下,我们通过逆推可以得到在什么情况下,7加上某个数等于11111111 11111111,结果即为状态2。
而11111111 11111111只需加1 便可将所有比特位清零。
故状态4,我们称之为-7在计算机中的表示,即-7的补码(在-7原码[10000000 00000111]基础上,符号位不变,每位取反,末位加一),故负数在计算机中的表示方式均是采用补码方式进行保存的。这就是我们进行正负数运算时得到零的过程。
在-7的补码状态时,若想得到-7的相反数(+7),我们需要采用连同符号位每位取反,末位加一的方法,来得到+7的原码表示。
当我们遇到下面的场景时,
char c = 'A';
short s = c;
cout << s << endl;
result is : 65由于char类型表示的是256个ascii字符,所以对其赋值可以是'A'、或者是65(但是内存始终表示的是[0100 0001])。而输出的结果只有一个,即'A'。
而将char类型的值赋值给short类型时,会出现如下变化,
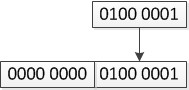
计算机会做位模式的拷贝,由于short类型本身为表示数字的类型,所以输出时不会进行字符的转译操作,故输出结果为65。
当过程相反时,
short s = 67;
char a = s;
cout << a << endl;输出结果为C, 原因如下
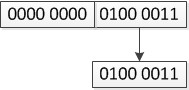
当大字节数赋给小字节数时,会将高位丢弃,而保留低位的比特。
再举一个例子:
int i = 2^23 + 2 ^ 21 + 2^14 + 7; //这样写是为了方便表达
short s = i;过程如下:
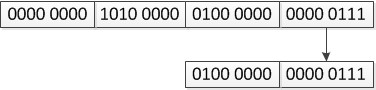
如图所示,这时计算机仅会进行位模式的简单拷贝,即丢弃高位,则数值大小改变。
如下这个负数的例子:
short s = -1;
int i = s;由于是小字节数复制给大字节数,在这个过程中,会进行符号位的扩展(负数用补码表示),如下图所示。
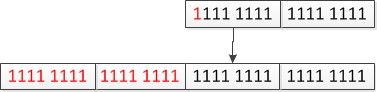
其赋值结果仍旧为-1。
在4字节32位中,我们如何来表示小数呢?
我们就要想办法,利用32位来构造出小数部分,看下图便知

我们可以采取逐步缩小正数部分,扩大分数部分的办法,来让计算机不断地渐进我们的小数值。
真正的浮点类型的结构如下所示:

高位的符号位我们记为s;
接下来的8比特表示无符号整型数,我们用exp表示(0~~255);
剩下的23比特表示小数,我们记为.xxxxxxxxxxx
浮点数的展开形式为:
移位操作的范围为2^-127 ~~~ 2^128,即化成标准形式的整数范围。
例如:
7.0的浮点表示,
我们需要展开成上述表达式的形式,则
7.0 * 2^0
3.5 * 2^1
1.75 * 2^2
则 exp=129, s=0 32位比特表示如下:
0 1000 0001 1100 0000 0000 0000 0000 000
我们将整形赋给浮点型时:
int i = 5;
float f = i;
cout << f << endl;输出为5, 但是需要将int类型的位模式,转化成浮点类型的位模式,即1.25 * 2^2 。
在下面的代码中,我们取得 i 变量的地址,将其转化为float指针类型,此时计算机内部并没有像上面一样进行位模式的转换,而是原封不动的保存着原本属于 i 的01序列,但此时的位模式已经属于浮点类型,故我们在输出结果时,得到的是一个奇小的数。
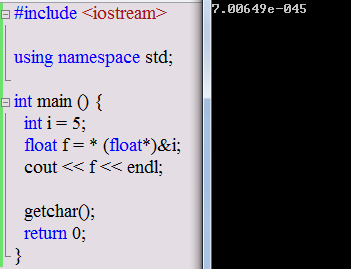
在4字节浮点类型的地址转化为short类型的指针时,输出结果如下:
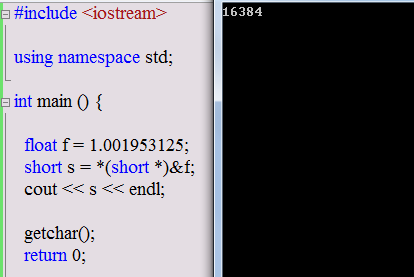
0.001953125 = 2 ^ -9
原因为:在此种方式下 float类型在转换成short类型时,不会做位模式的转换,而是直接将内存中的数据进行了读取,下图分大端模式和小端模式,在大端中,输出为0;在小端中,输出为16384(如笔者)。

如果单纯的是float类型转short类型,则需要将float类型进行4字节的位模式转换,在根据大小端进行位数的截取。介绍大小端存储的博客http://blog.csdn.net/ce123/article/details/6971544

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








