堆排序是一个优秀的算法,但是在实际应用中,如快速排序的性能会优于它。但是堆排序有着另外的作用,如优先队列;
与堆排序一样,优先队列也有两种形式:最大优先队列,最小优先队列(暂且讨论最大优先队列);
优先队列:是一种用来维护由一组元素构成的集合S的数据结果,其中的每个元素都有一个相关的值,称为关键字。
最大优先队列支持:
即:对最大优先队列进行插入,MaxHeapInsert;
返回最大优先队列的最大值,HeapMax;
去掉最大值并且返回该值,HeapExtractMax;
将第x个元素的值改为k,其中k>=x的原来的值,HeapIncreaseKey;
总之,即是在堆排序的基础上进行操作:
如返回最大值:
去掉最大值并且返回该值:
将第x个元素的值改为k,其中k>=x的原来的值:
最后还有一个插入:
代码:
#include <iostream>
#include <cstdlib>
using namespace std;
void MaxHeapIfy(int A[], int length, int i) //维护
{
int left = i * 2; //节点i的左孩子
int right = i * 2 + 1; //节点i的右孩子节点
int largest = i; //默认父节点
if (left <= length && A[largest] < A[left]) //左孩子比父节点大
{
largest = left;
}
if (right <= length && A[largest] < A[right]) //右孩子最大
{
largest = right;
}
if (i != largest) //最大值不是父节点
{
int temp = A[largest]; //exchange
A[largest] = A[i];
A[i] = temp;
MaxHeapIfy(A, length, largest); //继续维护
}
}
void BuildMaxHeap(int A[], int length) //建堆
{
for (int i = length / 2; i >= 1; i--)
{
MaxHeapIfy(A, length, i);
}
cout<<"建堆情况:"; //
for(int i = 1; i <= length; i++)
cout<<A[i]<<" ";
cout<<endl;
}
void HeapSort(int A[], int length) //堆排
{
int temp;
for(int i = length; i >= 2;)
{
temp = A[i]; //交换堆的第一个元素和堆的最后一个元素
A[i] = A[1];
A[1] = temp;
i--; //堆的大小减一
MaxHeapIfy(A, i, 1); //调堆
}
}
int HeapMax(int A[])
{
return A[1];
}
int HeapExtractMax(int A[], int &length)
{
if(length < 1)
{
cout<<"heap underflow";
return 0xffffffff;
}
int max = A[1];
A[1] = A[length];
length--;
MaxHeapIfy(A, length, 1);
cout<<"建堆情况:"; //
for(int i = 1; i <= length; i++)
cout<<A[i]<<" ";
cout<<endl;
return max;
}
void HeapIncreaseKey(int A[], int i, int key, int length) //将元素i的关键字值增加到K(假设k>=i的关键字值)
{
if(key < A[i])
{
cout<<"new key is smaller than current key";
//return 0;
}
A[i] = key;
while(i > 1 && A[i / 2] < A[i]) //插入值的父节点小于该值,更新
{
int temp = A[i];
A[i] = A[i / 2];
A[i / 2] = temp;
i = i / 2;
}
cout<<"建堆情况:"; //
for(int i = 1; i <= length; i++)
cout<<A[i]<<" ";
cout<<endl;
}
void MaxHeapInsert(int A[], int key, int &length) //插入
{
length++;
A[length] = -1;
HeapIncreaseKey(A, length, key, length);
}
void Show(int A[], int length) //输出排序效果
{
cout<<"排序结果:";
for(int i = 1; i <= length; i++) //cout
cout<<A[i]<<" ";
cout<<endl;
}
int main()
{
int A[] = {0, 4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
int length = sizeof(A) / sizeof(int) - 1; //
BuildMaxHeap(A, length); //建堆
int max = HeapMax(A); //返回最大值
cout<<"最大值是:"<<max<<endl;
max = HeapExtractMax(A, length); //去掉最大值,同时返回该值
cout<<"最大值是:"<<max<<endl;
int i, key;
i = 9; //第i个元素
key = 15; //关键值改变
HeapIncreaseKey(A, i, key, length); //改变关键值
MaxHeapInsert(A, 16, length); //插入值16
HeapSort(A, length); //排序
Show(A, length); //显示
return 0;
}
输出结果分析:
第一行:BuildMaxHeap(A, length);是对初始数据进行建堆的情况(int A[] = {0, 4, 1, 3, 2, 16, 9, 10, 14, 8, 7}中的A[0]元素只做填充效果);
第二行:int max = HeapMax(A); cout<<"最大值是:"<<max<<endl;通过HeapMax得到最大优先队列的最大值;
第三、四行: max = HeapExtractMax(A, length);cout<<"最大值是:"<<max<<endl;去掉最大值,输出此时的建堆情况,然后返回最大值并输出;
第五行:HeapIncreaceKey(A, i, key, length);//改变关键值,将第i个元素的值改为key,默认是key>=A[i],输出此时建堆情况;
第六行:MaxHeapInsert(A, 16, length);对最大优先队列插入值,重新建堆,输出;
第七行:HeapSort(A, length); Show(A, length);进行排序,并输出结果;
o(∩_∩)o







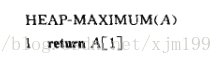


















 2279
2279

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








