【1、同余关系定义 (模n相等)】
Two integers a and b are said to be congruent modulo n , if their difference a − b is an integer multiple of n . An equivalent definition is that both numbers have the same remainder when divided by n. If this is the case, it is expressed as:
a ≡ b (mod n)
The above mathematical statement is read: "a is congruent to b modulo n ".
定义一、两个整数a和b被称作是"模n相等",当且仅当(a-b)的差是n的倍数。
定义二(和定义一是等价的)、如果a和b都去除以n,拥有相同的余数,那么则称a和b“关于模n时同余”,简称(“同余”)。
我们今后定义这种表达形式为:
a ≡ b (mod n) 表示“a和b模n相等”
For example,
- 38 ≡ 14 (mod 12)
because 38 − 14 = 24, which is a multiple of 12. For positive n and non-negative a and b , congruence of a and b can also be thought of as asserting that these two numbers have the same remainder after dividing by the modulus n . So,
例如: 38 ≡ 14 (mod 12) 我们可以称38和14模12相等(关于12同余),这是因为 38-14=24 是12的整数倍。当n是正数,a,b是非负数时,a和b的同余关系也可断言a和b都去除以n时,所得到的余数相等。
- 38 ≡ 2 (mod 12)
because both numbers, when divided by 12, have the same remainder (2). Equivalently, the fractional parts(小数部分) of doing a full division of each of the numbers by 12 are the same: .1666... (38/12 = 3.166..., 2/12 = .1666...). From the prior definition we also see that their difference, a - b = 36, is a whole number (integer ) multiple of 12 ( n = 12, 36/12 = 3).
(同样的或者认为: 38除以2的商的小数部分 和 2除以12的商的小数部分一样。)
【2、关于同余关系的定理】 (用定义一都比较容易证明)
The properties that make this relation a congruence relation (respecting addition, subtraction, and multiplication) are the following.
If  and
and  , then:
, then:
Applications
Modular arithmetic is referenced in number theory , group theory , ring theory , knot theory , abstract algebra , cryptography , computer science , chemistry and the visual and musical arts.
【3、欧拉函数】
3.1、定义(小于n,而且与n互质的非负数集合)
对于任何一个正整数n,我们定义小于n且和n互质 的非负整数构成的集合为Pn。
例如:
P1 = {0}
P2 = {0}
P5 = {0,2,3,4} (一定要除去自己和1以外;补上0)
P7= {0,2,3,4,5,6}
P8 = {0,3,5,6,7}
欧拉函数是数论中很重要的一个函数,欧拉函数是指:对于一个正整数n,小于n且和n互质 的非负整数的个数,记做:φ(n),其中φ(1)被定义为1,但是并没有任何实质的意义。
也就是φ(n) = |Pn|
例如:
φ(1)=1;φ(2)=1;φ(7)=6; φ(8)=5;
3.2 简单而有趣的一个结论
显然,对于素数p,φ(p)= p-1.
对于两个素数p、q,他们的乘积n = pq 满足 φ(n) =(p-1)(q-1)
证明:对于质数p,q,满足φ(n) =(p-1)(q-1)
考虑n的完全余数集Zn = { 1,2,....,pq -1} (所有可能的余数构成的集合),Pn的数据无非在Zn和{0}里面取
些数据{0,1,2,3,4,。。。,pq-2,pq-1}。所以: φ(n) < n 一定成立
这些数中而不和n互质的集合由下面三个集合的并构成:
1) 能够被p整除的集合{p,2p,3p,....,(q-1)p} 共计q-1个
2) 能够被q整除的集合{q,2q,3q,....,(p-1)q} 共计p-1个
3) {0}
很显然,1、2集合中没有共同的元素,Pn中元素个数 = pq - (p-1) - (q- 1) - 1 = (p-1)(q-1)
参考资源:
http://en.wikipedia.org/wiki/Modular_arithmetic
http://en.wikipedia.org/wiki/RSA#Operation
http://en.wikipedia.org/wiki/Congruence_relation
http://hi.baidu.com/cs85791075/blog/item/2586c02335f3ef519822ed4e.html (欧拉定理)
remainder 余数;
modular arithmetic 取模运算;
=======================================================================
密钥格式
=======================================================================
【1】数字证书、公钥和私钥这三者之间的关系是什么?
根据非对称密码学的原理,每个证书持有人都有一对公钥和私钥,这两把密钥可以互为加解密。公钥是公开的,不需要保密,而私钥是由证书持人自己持有,并且必须妥善保管和注意保密。数字证书则是由证书认证机构(CA)对证书申请者真实身份验证之后,用CA的根证书对申请人的一些基本信息以及申请人的公钥进行签名(相当于加盖发证书机构的公章)后形成的一个数字文件。 (如果我们在淘宝上开店,我们希望申请个证书。那么,我们肯定是想淘宝公司去申请(淘宝自己做自己的CA),我们填写一些信息,淘宝对我们的信息进行核实,核实通过后,淘宝以它的名义(就是淘宝对它自己颁发出去的证书都盖了这章)给我们签发证书。这个证书中含有了公钥。我不明白的是,申请者在提交申请表时,是不是自己已经准备好了一对配对的私钥和公钥,私钥留给了自己,而公钥做为申请表的填写内容提交给了CA机构?) CA完成签发 (比“颁发”好,“签发”的“签”表明了CA要用自己的私钥对证书进行签名,以标识该证书的确是本CA颁发出去的。)证书后,会将证书发布在CA的证书库(目录服务器)中,任何人都可以查询和下载,因此数字证书和公钥一样是公开的。
可以这样说,数字证书就是经过CA认证过的公钥 (证书中一个重要的信息点就是“公钥”),而私钥一般情况都是由证书持有者在自己本地生成的(这句话很费解,证书都已经颁发下来了,里面的公钥都已经固定了,私钥却能由证书持有人在自己本地生成?CA在签发证书时,并不产生该证书对应的私钥?) ,由证书持有者自己负责保管。具体使用时,签名操作是发送方用私钥进行签名,接受方用发送方证书来验证签名;加密操作则是用接受方的证书进行加密,接受方用自己的私钥进行解密。 因此,如果说数字证书是电子商务应用者的网上数字身份证话,那么证书相应的私钥则可以说是用户的私章或公章。
【2】公钥证书的定义
http://zhidao.baidu.com/question/58708378.html
英文:Public-key certificate
出处:ITU/T X.509 | ISO/IEC 9594-8:2001,GB/T 16264.8-2005
定义:用户(证书持有人,向CA机构申请证书的人)的公钥连同“其他信息”(用户的描述信息),并由发布该证书的证书认证机构的私钥进行签名盖章使其不可伪造。
解释:公钥证书的最主要功能是实现了用户身份与用户公钥的绑定,而这种绑定的真实性则是通过CA的签名来保证的。(证书和公钥的关系: 证书是为了解决公钥的发布和信任的问题。一个主体(比如企业)要对外公布它的公钥,总不可能仅仅发些二进制数据,否则谁知道这个公钥属于哪个主体,所以肯定要附带一些附加信息来标识这个公钥是属于某个主体的。接着我们会问,某个主体对外公布它自己的公钥会不会骗人呀或者会不会存在其他主体冒充它对外公布一个公钥呢?于是,我们希望有个第三方的认证机构,来核实并担保这种绑定关系“也就是“用户公钥和用户身份信息的绑定关系””。在技术实现上就是通过一个载体(比如文件),将用户公钥和用户身份描述信息同时绑定存储到该文件中。而且,为了让大家相信这种绑定关系的真实性,CA用自己的私钥在这个数字文件中盖章。这样一来,一个证书就包括了至少三方面的信息: 用户公钥,用户身份信息,CA机构盖章。 另外,为了CA机构方便管理众多用户的证书,CA在制作证书时,还会额外的加入些证书本身的属性信息,比如:版本号,有效期,证书文件的编码方式呀,证书序列号呀(以方便检索呀,证书的序列号,CA 应保证该序列号是唯一的 )。) 定义中所说的“其他信息”主要就是指用户身份信息,为了进一步说明这种绑定关系,还包含版本号、证书序列号、有效期、颁发者身份等。在V3版证书中,又增加了很多扩展项信息。
【3】一个证书颁发下来后,用户怎么去使用呢?
在证书中标识的密钥对(公钥及相关的私钥)的用法。
【4】一个证书到底包含了哪些信息?
证书提供了一个在公钥和拥有相应私钥的实体之间建立关系的机制。 目前最常用的证书格式通过 ITU-T X.509 版本 3 (X.509v3) 国际标准定义。RFC 2459 是 X.509v3 的一个配置文件,进一步阐明了 X.509v3 中定义的字段。Windows 2000 PKI 采用 X.509v3 标准。Windows 证书是按照 RFC 2459 中的说明编程的,但仍然叫做 X.509v3 证书。(有关 ITU-T X.509 的详细信息,请参见“Windows 2000 证书服务”白皮书。)
【5】生活中上网,一般什么时候会涉及到和数字证书有关的内容呢?
可以为各种目的颁发证书,如 Web 用户身份验证、Web 服务器身份验证、使用安全/多用途 Internet 邮件扩充协议 (Secure/Multipurpose Internet Mail Extensions, S/MIME) 的安全电子邮件、IP 安全性 (IP Security)、安全套接字协议层/事务层安全性 (Secure Sockets Layer/Transaction Layer Security, SSL/TLS ) 和代码签名。如果在一个组织内部使用 Windows 2000 企业证书颁发机构(在“Windows 2000 Certificate Services”白皮书中说明),证书可用于登录到 Windows 2000 域。证书还可以由一个 CA 颁发给另一个 CA,以建立证书层次结构。









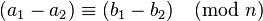
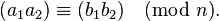
















 5053
5053

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








