一、基本术语
图：由有穷、非空点集和边集合组成，简写成G(V,E);
Vertex：图中的顶点；
无向图：图中每条边都没有方向；
有向图：图中每条边都有方向；
无向边：边是没有方向的，写为(a,b)
有向边：边是有方向的，写为<a,b>
有向边也成为弧；开始顶点称为弧尾，结束顶点称为弧头；
简单图：不存在指向自己的边、不存在两条重复的边的图；
无向完全图：每个顶点之间都有一条边的无向图；
有向完全图：每个顶点之间都有两条互为相反的边的无向图；
稀疏图：边相对于顶点来说很少的图；
稠密图：边很多的图；
权重：图中的边可能会带有一个权重，为了区分边的长短；
网：带有权重的图；
度：与特定顶点相连接的边数；
出度、入度：对于有向图的概念，出度表示此顶点为起点的边的数目，入度表示此顶点为终点的边的数目；
环：第一个顶点和最后一个顶点相同的路径；
简单环：除去第一个顶点和最后一个顶点后没有重复顶点的环；
连通图：任意两个顶点都相互连通的图；
极大连通子图：包含竟可能多的顶点（必须是连通的），即找不到另外一个顶点，使得此顶点能够连接到此极大连通子图的任意一个顶点；
连通分量：极大连通子图的数量；
强连通图：此为有向图的概念，表示任意两个顶点a，b，使得a能够连接到b，b也能连接到a 的图；
生成树：n个顶点，n-1条边，并且保证n个顶点相互连通（不存在环）；
最小生成树：此生成树的边的权重之和是所有生成树中最小的；
AOV网：结点表示活动的网；
AOE网：边表示活动的持续时间的网；
二、图的存储结构
1.邻接矩阵
维持一个二维数组，arr[i][j]表示i到j的边，如果两顶点之间存在边，则为1，否则为0；
维持一个一维数组，存储顶点信息，比如顶点的名字；
下图为一般的有向图：
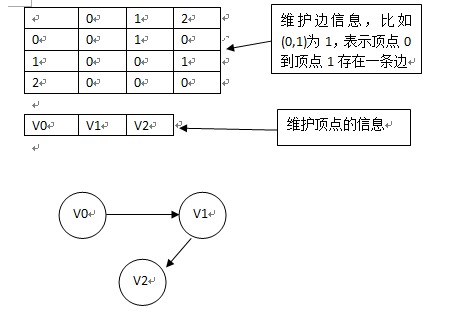
注意：如果我们要看vi节点邻接的点，则只需要遍历arr[i]即可；
下图为带有权重的图的邻接矩阵表示法：
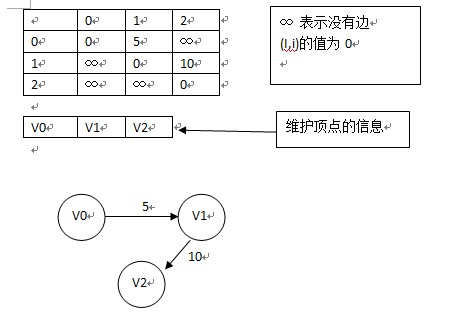
缺点：邻接矩阵表示法对于稀疏图来说不合理，因为太浪费空间；
2.邻接表
如果图示一般的图，则如下图：
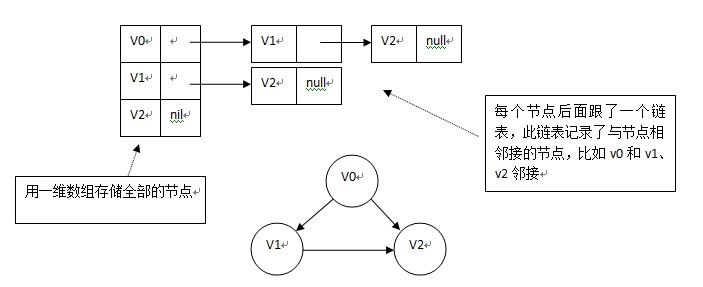
如果是网，即边带有权值，则如下图：
3.十字链表
只针对有向图；，适用于计算出度和入度；
顶点结点：
边结点：
好处：创建的时间复杂度和邻接链表相同，但是能够同时计算入度和出度；
4.邻接多重表
针对无向图； 如果我们只是单纯对节点进行操作，则邻接表是一个很好的选择，但是如果我们要在邻接表中删除一条边，则需要删除四个顶点（因为无向图）；
在邻接多重表中，只需要删除一个节点，即可完成边的删除，因此比较方便；
因此邻接多重表适用于对边进行删除的操作；
顶点节点和邻接表没区别，边表节点如下图：
比如：
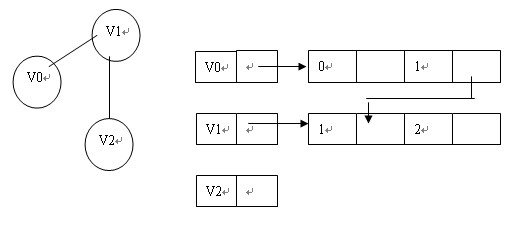
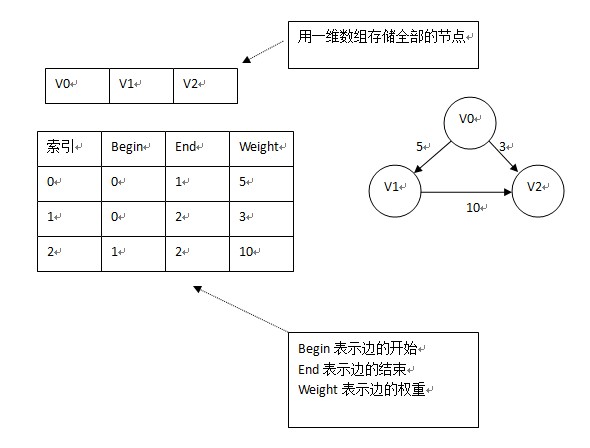
5.边集数组
适合依次对边进行操作；
存储边的信息，如下图：
三、图的遍历
DFS
思想：往深里遍历，如果不能深入，则回朔；
比如：
BFS
思想：对所有邻接节点遍历；
/** * O(v+e) */ @Test public void BFS() { ArrayList<Integer> list = new ArrayList<Integer>(); for (int i = 0; i < g.nodes.length; i++) { if (!visited[i]) { visited[i] = true; list.add(i); System.out.println(i); while (!list.isEmpty()) { int k = list.remove(0); EdgeNode current = g.nodes[k].next; while (current != null) { if (!visited[current.idx]) { visited[current.idx] = true; System.out.println(current.idx); list.add(current.idx); } current = current.next; } } } } }四、最小生成树
prim
邻接矩阵存储；
/** * 时间复杂度为O(n^2) * 适用于稠密图 */ @Test public void prim(){ int cost[] = new int[9]; int pre[] = new int[9]; for(int i=0;i<g1.vertex.length;i++){ cost[i] = g1.adjMatrix[0][i]; } cost[0] = 0; for(int i=1;i<g1.vertex.length;i++){ int min = 65536; int k = 0; for(int j=1;j<g1.vertex.length;j++){ if(cost[j]!=0&&cost[j]<min){ min = cost[j]; k = j; } } cost[k] = 0; System.out.println(pre[k]+","+k); for(int j=1;j<g1.vertex.length;j++){ if(cost[j]!=0&&g1.adjMatrix[k][j]<cost[j]){ pre[j] = k; cost[j] = g1.adjMatrix[k][j]; } } } }
krustral
边集数组存储；
/** * 时间复杂度：O(eloge) * 适用于稀疏图 */ @Test public void krustral(){ Edge[] edges = initEdges(); int parent[] = new int[9]; for(int i=0;i<edges.length;i++){ Edge edge = edges[i]; int m = find(parent,edge.begin); int n = find(parent,edge.end); if(m!=n){ parent[m] = n; System.out.println(m+","+n); } } } private static int find(int[] parent, int f) { while (parent[f] > 0) { f = parent[f]; } return f; }
五、最短路径
dijkstra算法
邻接矩阵存储；
//O（n^2） @Test public void Dijkstra(){ int distance[] = new int[9]; int pre[] = new int[9]; boolean finished[] = new boolean[9]; finished[0] = true; for(int i=0;i<9;i++){ distance[i] = g1.adjMatrix[0][i]; } int k = 0; for(int i=1;i<9;i++){ int min = 65536; for(int j=0;j<9;j++){ if(!finished[j]&&distance[j]<min){ min = distance[j]; k = j; } } finished[k] = true; System.out.println(pre[k]+","+k); for(int j=1;j<9;j++){ if(!finished[j]&&(min+g1.adjMatrix[k][j])<distance[j]){ distance[j] = min+g1.adjMatrix[k][j]; pre[j] = k; } } } }
Floyd
使用：
(1)邻接矩阵：存储图；
/** * O(n^3) * 求出任意顶点之间的距离 */ @Test public void floyd(Graph1 g) { int i, j, k; int length = g.vertex.length; int dist[][] = new int[length][length]; int pre[][] = new int[length][length]; for (i = 0; i < g.vertex.length; i++) { for (j = 0; j < g.vertex.length; j++) { pre[i][j] = j; dist[i][j] = g.adjMatrix[i][j]; } } for (i = 0; i < length; i++) { for (j = 0; j < g.vertex.length; j++) { for (k = 0; k < g.vertex.length; k++) { if (dist[i][j] > dist[i][k] + dist[k][j]) { dist[i][j] = dist[i][k] + dist[k][j]; pre[i][j] = pre[i][k]; } } } } System.out.println(); }
六、拓扑排序
使用数据结构：
(1)栈：用来存放入度为0的节点；
(2)变种邻接列表：作为图的存储结构；此邻接列表的顶点节点还需要存放入度属性；
/** * O(n+e) */ private static String topologicalSort(Graph2 g2) { Stack<Integer> s = new Stack<Integer>(); int count = 0; for(int i=0;i<g2.nodes.length;i++){ if(g2.nodes[i].indegree==0){ s.push(i); } } while(!s.isEmpty()){ int value = s.pop(); System.out.println(value+"、"); count++; EdgeNode node = g2.nodes[value].next; while(node!=null){ g2.nodes[node.idx].indegree--; if(g2.nodes[node.idx].indegree==0){ s.push(node.idx); } node = node.next; } } if(count<g2.nodes.length){ return "error"; } return "ok"; }七、关键路径
使用数据结构：
(1)变种邻接列表：同拓扑排序；
(2)变量：
ltv表示某个事件的最晚开始时间；
etv表示事件最早开始时间；
ete表示活动最早开始时间；
lte表示活动最晚开始时间；
//O（n+e）
@Test public void CriticalPath(){ Stack<Integer> stack = topological_etv(); int length = stack.size(); if(stack==null){ return ; } else{ int[]ltv = new int[length]; for(int i=0;i<stack.size();i++){ ltv[i] = etv[stack.size()-1]; } //从拓扑排序的最后开始计算ltv while(!stack.isEmpty()){ int top = stack.pop(); EdgeNode current = g.nodes[top].next; while(current!=null){ int idx = current.idx; //最晚发生时间要取所有活动中最早的 if((ltv[idx]-current.weight)<ltv[top]){ ltv[top] = ltv[idx]-current.weight; } } } int ete = 0; int lte = 0; for(int j=0;j<length;j++){ EdgeNode current = g.nodes[j].next; while(current!=null){ int idx = current.idx; ete = etv[j]; lte = ltv[idx]-current.weight; if(ete==lte){ //是关键路径 } } } } } private Stack<Integer> topological_etv(){ Stack<Integer> stack2 = new Stack<Integer>(); Stack<Integer>stack1 = new Stack<Integer>(); for(int i=0;i<g.nodes.length;i++){ if(g.nodes[i].indegree==0){ stack1.add(i); } } etv[] = new int[g.nodes.length]; int count = 0; while(!stack1.isEmpty()){ int top = stack1.pop(); count++; stack2.push(top); EdgeNode current = g.nodes[top].next; while(current!=null){ int idx = current.idx; if((--g.nodes[idx].indegree)==0){ stack1.push(idx); } if((etv[top]+current.weight)>etv[idx]){ etv[idx] = etv[top]+current.weight; } current = current.next; } } if(count<g.nodes.length){ return null; } return stack2; }
扫一扫
613
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
