Android中图像变换Matrix的原理应用

第一部分 Matrix的数学原理

在Android中，如果你用Matrix进行过图像处理，那么一定知道Matrix这个类。Android中的Matrix是一个3 x 3的矩阵，其内容如下：

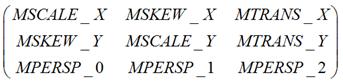
Matrix的对图像的处理可分为四类基本变换：

Translate 平移变换

Rotate 旋转变换

Scale 缩放变换

Skew 错切变换

从字面上理解，矩阵中的MSCALE用于处理缩放变换，MSKEW用于处理错切变换，MTRANS用于处理平移变换，MPERSP用于处理透视变换。实际中当然不能完全按照字面上的说法去理解Matrix。同时，在Android的文档中，未见到用Matrix进行透视变换的相关说明，所以本文也不讨论这方面的问题。

针对每种变换，Android提供了pre、set和post三种操作方式。其中

set用于设置Matrix中的值。

pre是先乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。先乘相当于矩阵运算中的右乘。

post是后乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。后乘相当于矩阵运算中的左乘。

除平移变换(Translate)外，旋转变换(Rotate)、缩放变换(Scale)和错切变换(Skew)都可以围绕一个中心点来进行，如果不指定，在默认情况下是围绕(0, 0)来进行相应的变换的。

下面我们来看看四种变换的具体情形。由于所有的图形都是有点组成，因此我们只需要考察一个点相关变换即可。

一、 平移变换

假定有一个点的坐标是，将其移动到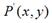，再假定在x轴和y轴方向移动的大小分别为：

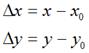
如下图所示：

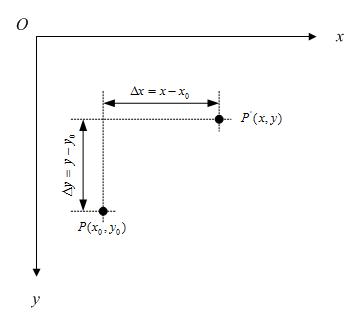
不难知道：

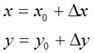
如果用矩阵来表示的话，就可以写成：

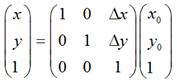
二、 旋转变换

2.1 围绕坐标原点旋转：

假定有一个点，相对坐标原点顺时针旋转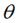后的情形，同时假定P点离坐标原点的距离为r，如下图：

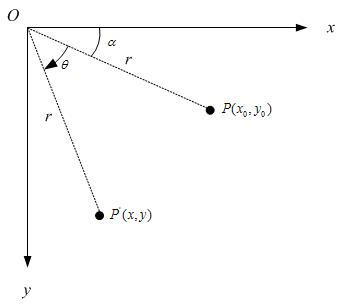
那么，

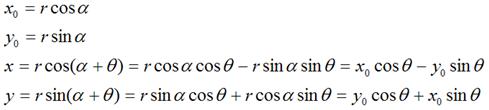
如果用矩阵，就可以表示为：

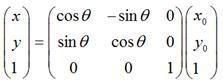
2.2 围绕某个点旋转

如果是围绕某个点顺时针旋转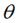，那么可以用矩阵表示为：

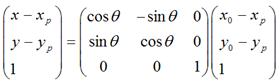
可以化为：

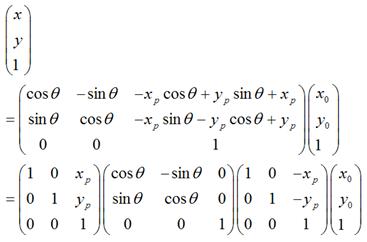
很显然，

1.

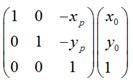是将坐标原点移动到点后，的新坐标。

2.

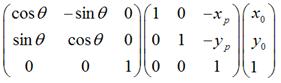
是将上一步变换后的，围绕新的坐标原点顺时针旋转。

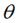3.

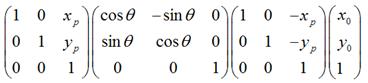
经过上一步旋转变换后，再将坐标原点移回到原来的坐标原点。

所以，围绕某一点进行旋转变换，可以分成3个步骤，即首先将坐标原点移至该点，然后围绕新的坐标原点进行旋转变换，再然后将坐标原点移回到原先的坐标原点。

三、 缩放变换

理论上而言，一个点是不存在什么缩放变换的，但考虑到所有图像都是由点组成，因此，如果图像在x轴和y轴方向分别放大k1和k2倍的话，那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍，即

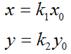
用矩阵表示就是：

缩放变换比较好理解，就不多说了。

四、 错切变换

错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并)，它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变，而对应的y坐标(或者x坐标)则按比例发生平移，且平移的大小和该点到x轴(或y轴)的垂直距离成正比。错切变换，属于等面积变换，即一个形状在错切变换的前后，其面积是相等的。

比如下图，各点的y坐标保持不变，但其x坐标则按比例发生了平移。这种情况将水平错切。

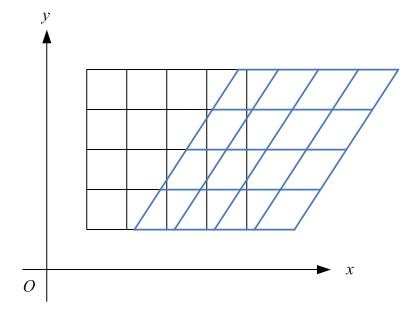
下图各点的x坐标保持不变，但其y坐标则按比例发生了平移。这种情况叫垂直错切。

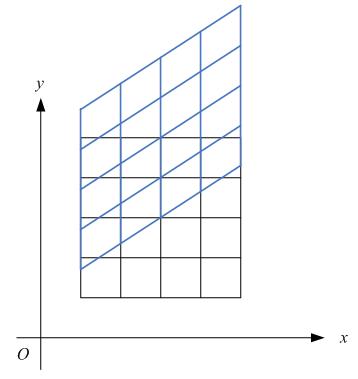
假定一个点经过错切变换后得到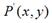，对于水平错切而言，应该有如下关系：

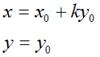
用矩阵表示就是：

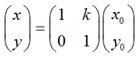
扩展到3 x 3的矩阵就是下面这样的形式：

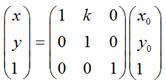
同理，对于垂直错切，可以有：

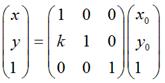
在数学上严格的错切变换就是上面这样的。在Android中除了有上面说到的情况外，还可以同时进行水平、垂直错切，那么形式上就是：

五、 对称变换

除了上面讲到的4中基本变换外，事实上，我们还可以利用Matrix，进行对称变换。所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如，某点经过对称变换后得到，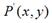

如果对称轴是x轴，难么，

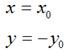
用矩阵表示就是：

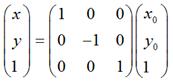
如果对称轴是y轴，那么，

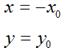
用矩阵表示就是：

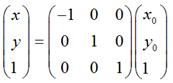
如果对称轴是y = x，如图：

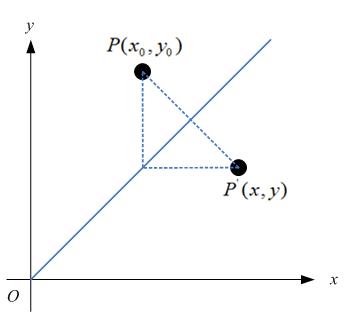
那么，

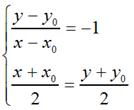
很容易可以解得：

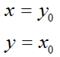
用矩阵表示就是：

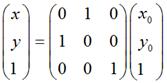
同样的道理，如果对称轴是y = -x，那么用矩阵表示就是：

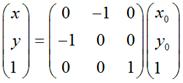
特殊地，如果对称轴是y = kx，如下图：

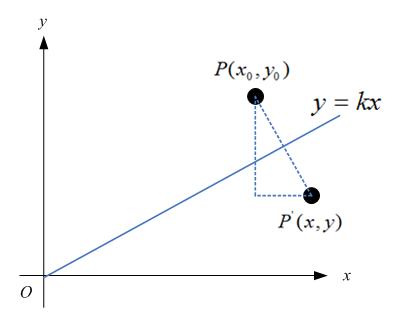
那么，

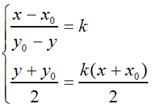
很容易可解得：

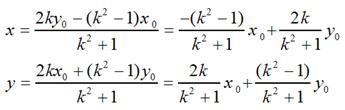
用矩阵表示就是：

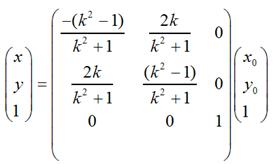
当k = 0时，即y = 0，也就是对称轴为x轴的情况；当k趋于无穷大时，即x = 0，也就是对称轴为y轴的情况；当k =1时，即y = x，也就是对称轴为y = x的情况；当k = -1时，即y = -x，也就是对称轴为y = -x的情况。不难验证，这和我们前面说到的4中具体情况是相吻合的。

如果对称轴是y = kx + b这样的情况，只需要在上面的基础上增加两次平移变换即可，即先将坐标原点移动到(0, b)，然后做上面的关于y = kx的对称变换，再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的：

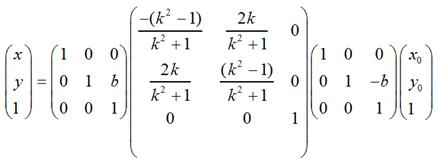
需要特别注意：在实际编程中，我们知道屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的，所以在数学上y = x和屏幕上的y = -x才是真正的同一个东西，反之亦然。也就是说，如果要使图片在屏幕上看起来像按照数学意义上y = x对称，那么需使用这种转换：

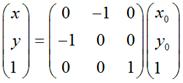
要使图片在屏幕上看起来像按照数学意义上y = -x对称，那么需使用这种转换：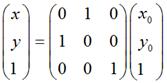

关于对称轴为y = kx或y = kx + b的情况，同样需要考虑这方面的问题。

第二部分 代码验证

在第一部分中讲到的各种图像变换的验证代码如下，一共列出了10种情况。如果要验证其中的某一种情况，只需将相应的代码反注释即可。试验中用到的图片：

其尺寸为162 x 251。

每种变换的结果，请见代码之后的说明。

[java] view plain copy

1. <spanstyle="font-size:13px;"></span><prename="code"class="java">packagecom.pat.testtransformmatrix;
3. importandroid.app.Activity;
4. importandroid.content.Context;
5. importandroid.graphics.Bitmap;
6. importandroid.graphics.BitmapFactory;
7. importandroid.graphics.Canvas;
8. importandroid.graphics.Matrix;
9. importandroid.os.Bundle;
10. importandroid.util.Log;
11. importandroid.view.MotionEvent;
12. importandroid.view.View;
13. importandroid.view.Window;
14. importandroid.view.WindowManager;
15. importandroid.view.View.OnTouchListener;
16. importandroid.widget.ImageView;
18. publicclassTestTransformMatrixActivityextendsActivity
19. implements
20. OnTouchListener
21. {
22. privateTransformMatrixViewview;
23. @Override
24. publicvoidonCreate(BundlesavedInstanceState)
25. {
26. super.onCreate(savedInstanceState);
27. requestWindowFeature(Window.FEATURE_NO_TITLE);
28. this.getWindow().setFlags(WindowManager.LayoutParams.FLAG_FULLSCREEN,WindowManager.LayoutParams.FLAG_FULLSCREEN);
30. view=newTransformMatrixView(this);
31. view.setScaleType(ImageView.ScaleType.MATRIX);
32. view.setOnTouchListener(this);
34. setContentView(view);
35. }
37. classTransformMatrixViewextendsImageView
38. {
39. privateBitmapbitmap;
40. privateMatrixmatrix;
41. publicTransformMatrixView(Contextcontext)
42. {
43. super(context);
44. bitmap=BitmapFactory.decodeResource(getResources(),R.drawable.sophie);
45. matrix=newMatrix();
46. }
48. @Override
49. protectedvoidonDraw(Canvascanvas)
50. {
51. //画出原图像
52. canvas.drawBitmap(bitmap,0,0,null);
53. //画出变换后的图像
54. canvas.drawBitmap(bitmap,matrix,null);
55. super.onDraw(canvas);
56. }
58. @Override
59. publicvoidsetImageMatrix(Matrixmatrix)
60. {
61. this.matrix.set(matrix);
62. super.setImageMatrix(matrix);
63. }
65. publicBitmapgetImageBitmap()
66. {
67. returnbitmap;
68. }
69. }
71. publicbooleanonTouch(Viewv,MotionEvente)
72. {
73. if(e.getAction()==MotionEvent.ACTION_UP)
74. {
75. Matrixmatrix=newMatrix();
76. //输出图像的宽度和高度(162x251)
77. Log.e("TestTransformMatrixActivity","imagesize:widthxheight="+view.getImageBitmap().getWidth()+"x"+view.getImageBitmap().getHeight());
78. //1.平移
79. matrix.postTranslate(view.getImageBitmap().getWidth(),view.getImageBitmap().getHeight());
80. //在x方向平移view.getImageBitmap().getWidth()，在y轴方向view.getImageBitmap().getHeight()
81. view.setImageMatrix(matrix);
83. //下面的代码是为了查看matrix中的元素
84. float[]matrixValues=newfloat[9];
85. matrix.getValues(matrixValues);
86. for(inti=0;i<3;++i)
87. {
88. Stringtemp=newString();
89. for(intj=0;j<3;++j)
90. {
91. temp+=matrixValues[3*i+j]+"\t";
92. }
93. Log.e("TestTransformMatrixActivity",temp);
94. }
97. 2.旋转(围绕图像的中心点)
98. //matrix.setRotate(45f,view.getImageBitmap().getWidth()/2f,view.getImageBitmap().getHeight()/2f);
99. //
100. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
101. //matrix.postTranslate(view.getImageBitmap().getWidth()*1.5f,0f);
102. //view.setImageMatrix(matrix);
103. //
104. 下面的代码是为了查看matrix中的元素
105. //float[]matrixValues=newfloat[9];
106. //matrix.getValues(matrixValues);
107. //for(inti=0;i<3;++i)
108. //{
109. //Stringtemp=newString();
110. //for(intj=0;j<3;++j)
111. //{
112. //temp+=matrixValues[3*i+j]+"\t";
113. //}
114. //Log.e("TestTransformMatrixActivity",temp);
115. //}
118. 3.旋转(围绕坐标原点)+平移(效果同2)
119. //matrix.setRotate(45f);
120. //matrix.preTranslate(-1f*view.getImageBitmap().getWidth()/2f,-1f*view.getImageBitmap().getHeight()/2f);
121. //matrix.postTranslate((float)view.getImageBitmap().getWidth()/2f,(float)view.getImageBitmap().getHeight()/2f);
122. //
123. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
124. //matrix.postTranslate((float)view.getImageBitmap().getWidth()*1.5f,0f);
125. //view.setImageMatrix(matrix);
126. //
127. 下面的代码是为了查看matrix中的元素
128. //float[]matrixValues=newfloat[9];
129. //matrix.getValues(matrixValues);
130. //for(inti=0;i<3;++i)
131. //{
132. //Stringtemp=newString();
133. //for(intj=0;j<3;++j)
134. //{
135. //temp+=matrixValues[3*i+j]+"\t";
136. //}
137. //Log.e("TestTransformMatrixActivity",temp);
138. //}
140. 4.缩放
141. //matrix.setScale(2f,2f);
142. 下面的代码是为了查看matrix中的元素
143. //float[]matrixValues=newfloat[9];
144. //matrix.getValues(matrixValues);
145. //for(inti=0;i<3;++i)
146. //{
147. //Stringtemp=newString();
148. //for(intj=0;j<3;++j)
149. //{
150. //temp+=matrixValues[3*i+j]+"\t";
151. //}
152. //Log.e("TestTransformMatrixActivity",temp);
153. //}
154. //
155. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
156. //matrix.postTranslate(view.getImageBitmap().getWidth(),view.getImageBitmap().getHeight());
157. //view.setImageMatrix(matrix);
158. //
159. 下面的代码是为了查看matrix中的元素
160. //matrixValues=newfloat[9];
161. //matrix.getValues(matrixValues);
162. //for(inti=0;i<3;++i)
163. //{
164. //Stringtemp=newString();
165. //for(intj=0;j<3;++j)
166. //{
167. //temp+=matrixValues[3*i+j]+"\t";
168. //}
169. //Log.e("TestTransformMatrixActivity",temp);
170. //}
173. 5.错切-水平
174. //matrix.setSkew(0.5f,0f);
175. 下面的代码是为了查看matrix中的元素
176. //float[]matrixValues=newfloat[9];
177. //matrix.getValues(matrixValues);
178. //for(inti=0;i<3;++i)
179. //{
180. //Stringtemp=newString();
181. //for(intj=0;j<3;++j)
182. //{
183. //temp+=matrixValues[3*i+j]+"\t";
184. //}
185. //Log.e("TestTransformMatrixActivity",temp);
186. //}
187. //
188. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
189. //matrix.postTranslate(view.getImageBitmap().getWidth(),0f);
190. //view.setImageMatrix(matrix);
191. //
192. 下面的代码是为了查看matrix中的元素
193. //matrixValues=newfloat[9];
194. //matrix.getValues(matrixValues);
195. //for(inti=0;i<3;++i)
196. //{
197. //Stringtemp=newString();
198. //for(intj=0;j<3;++j)
199. //{
200. //temp+=matrixValues[3*i+j]+"\t";
201. //}
202. //Log.e("TestTransformMatrixActivity",temp);
203. //}
205. 6.错切-垂直
206. //matrix.setSkew(0f,0.5f);
207. 下面的代码是为了查看matrix中的元素
208. //float[]matrixValues=newfloat[9];
209. //matrix.getValues(matrixValues);
210. //for(inti=0;i<3;++i)
211. //{
212. //Stringtemp=newString();
213. //for(intj=0;j<3;++j)
214. //{
215. //temp+=matrixValues[3*i+j]+"\t";
216. //}
217. //Log.e("TestTransformMatrixActivity",temp);
218. //}
219. //
220. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
221. //matrix.postTranslate(0f,view.getImageBitmap().getHeight());
222. //view.setImageMatrix(matrix);
223. //
224. 下面的代码是为了查看matrix中的元素
225. //matrixValues=newfloat[9];
226. //matrix.getValues(matrixValues);
227. //for(inti=0;i<3;++i)
228. //{
229. //Stringtemp=newString();
230. //for(intj=0;j<3;++j)
231. //{
232. //temp+=matrixValues[3*i+j]+"\t";
233. //}
234. //Log.e("TestTransformMatrixActivity",temp);
235. //}
237. //7.错切-水平+垂直
238. //matrix.setSkew(0.5f,0.5f);
239. 下面的代码是为了查看matrix中的元素
240. //float[]matrixValues=newfloat[9];
241. //matrix.getValues(matrixValues);
242. //for(inti=0;i<3;++i)
243. //{
244. //Stringtemp=newString();
245. //for(intj=0;j<3;++j)
246. //{
247. //temp+=matrixValues[3*i+j]+"\t";
248. //}
249. //Log.e("TestTransformMatrixActivity",temp);
250. //}
251. //
252. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
253. //matrix.postTranslate(0f,view.getImageBitmap().getHeight());
254. //view.setImageMatrix(matrix);
255. //
256. 下面的代码是为了查看matrix中的元素
257. //matrixValues=newfloat[9];
258. //matrix.getValues(matrixValues);
259. //for(inti=0;i<3;++i)
260. //{
261. //Stringtemp=newString();
262. //for(intj=0;j<3;++j)
263. //{
264. //temp+=matrixValues[3*i+j]+"\t";
265. //}
266. //Log.e("TestTransformMatrixActivity",temp);
267. //}
269. 8.对称(水平对称)
270. //floatmatrix_values[]={1f,0f,0f,0f,-1f,0f,0f,0f,1f};
271. //matrix.setValues(matrix_values);
272. 下面的代码是为了查看matrix中的元素
273. //float[]matrixValues=newfloat[9];
274. //matrix.getValues(matrixValues);
275. //for(inti=0;i<3;++i)
276. //{
277. //Stringtemp=newString();
278. //for(intj=0;j<3;++j)
279. //{
280. //temp+=matrixValues[3*i+j]+"\t";
281. //}
282. //Log.e("TestTransformMatrixActivity",temp);
283. //}
284. //
285. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
286. //matrix.postTranslate(0f,view.getImageBitmap().getHeight()*2f);
287. //view.setImageMatrix(matrix);
288. //
289. 下面的代码是为了查看matrix中的元素
290. //matrixValues=newfloat[9];
291. //matrix.getValues(matrixValues);
292. //for(inti=0;i<3;++i)
293. //{
294. //Stringtemp=newString();
295. //for(intj=0;j<3;++j)
296. //{
297. //temp+=matrixValues[3*i+j]+"\t";
298. //}
299. //Log.e("TestTransformMatrixActivity",temp);
300. //}
302. 9.对称-垂直
303. //floatmatrix_values[]={-1f,0f,0f,0f,1f,0f,0f,0f,1f};
304. //matrix.setValues(matrix_values);
305. 下面的代码是为了查看matrix中的元素
306. //float[]matrixValues=newfloat[9];
307. //matrix.getValues(matrixValues);
308. //for(inti=0;i<3;++i)
309. //{
310. //Stringtemp=newString();
311. //for(intj=0;j<3;++j)
312. //{
313. //temp+=matrixValues[3*i+j]+"\t";
314. //}
315. //Log.e("TestTransformMatrixActivity",temp);
316. //}
317. //
318. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
319. //matrix.postTranslate(view.getImageBitmap().getWidth()*2f,0f);
320. //view.setImageMatrix(matrix);
321. //
322. 下面的代码是为了查看matrix中的元素
323. //matrixValues=newfloat[9];
324. //matrix.getValues(matrixValues);
325. //for(inti=0;i<3;++i)
326. //{
327. //Stringtemp=newString();
328. //for(intj=0;j<3;++j)
329. //{
330. //temp+=matrixValues[3*i+j]+"\t";
331. //}
332. //Log.e("TestTransformMatrixActivity",temp);
333. //}
336. 10.对称(对称轴为直线y=x)
337. //floatmatrix_values[]={0f,-1f,0f,-1f,0f,0f,0f,0f,1f};
338. //matrix.setValues(matrix_values);
339. 下面的代码是为了查看matrix中的元素
340. //float[]matrixValues=newfloat[9];
341. //matrix.getValues(matrixValues);
342. //for(inti=0;i<3;++i)
343. //{
344. //Stringtemp=newString();
345. //for(intj=0;j<3;++j)
346. //{
347. //temp+=matrixValues[3*i+j]+"\t";
348. //}
349. //Log.e("TestTransformMatrixActivity",temp);
350. //}
351. //
352. 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
353. //matrix.postTranslate(view.getImageBitmap().getHeight()+view.getImageBitmap().getWidth(),
354. //view.getImageBitmap().getHeight()+view.getImageBitmap().getWidth());
355. //view.setImageMatrix(matrix);
356. //
357. 下面的代码是为了查看matrix中的元素
358. //matrixValues=newfloat[9];
359. //matrix.getValues(matrixValues);
360. //for(inti=0;i<3;++i)
361. //{
362. //Stringtemp=newString();
363. //for(intj=0;j<3;++j)
364. //{
365. //temp+=matrixValues[3*i+j]+"\t";
366. //}
367. //Log.e("TestTransformMatrixActivity",temp);
368. //}
370. view.invalidate();
371. }
372. returntrue;
373. }
374. }</pre><br>
375. <br>
376. <p><spanstyle="font-size:13px"></span></p>
377. <p><spanstyle="font-size:13px">下面给出上述代码中，各种变换的具体结果及其对应的相关变换矩阵</span></p>
378. <p><spanstyle="font-size:13px">1.平移</span></p>
379. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321712352qQRu.gif"alt=""></span></p>
380. <p><spanstyle="font-size:13px">输出的结果：</span></p>
381. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217123565Wwz.gif"alt=""></span></p>
382. <p><spanstyle="font-size:13px">请对照第一部分中的“一、平移变换”所讲的情形，考察上述矩阵的正确性。</span></p>
383. <p><spanstyle="font-size:13px"></span></p>
384. <p><spanstyle="font-size:13px">2.旋转(围绕图像的中心点)</span></p>
385. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_132171250556xp.gif"alt=""></span></p>
386. <p><spanstyle="font-size:13px">输出的结果：</span></p>
387. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321712512Yj1i.gif"alt=""></span></p>
388. <p><spanstyle="font-size:13px">它实际上是</span></p>
389. <p><spanstyle="font-size:13px">matrix.setRotate(45f,view.getImageBitmap().getWidth()/2f,view.getImageBitmap().getHeight()/2f);</span></p>
390. <p><spanstyle="font-size:13px">matrix.postTranslate(view.getImageBitmap().getWidth()*1.5f,0f);</span></p>
391. <p><spanstyle="font-size:13px">这两条语句综合作用的结果。根据第一部分中“二、旋转变换”里面关于围绕某点旋转的公式，</span></p>
392. <p><spanstyle="font-size:13px">matrix.setRotate(45f,view.getImageBitmap().getWidth()/2f,view.getImageBitmap().getHeight()/2f);</span></p>
393. <p><spanstyle="font-size:13px">所产生的转换矩阵就是：</span></p>
394. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321712644I54M.gif"alt=""></span></p>
395. <p><spanstyle="font-size:13px">而matrix.postTranslate(view.getImageBitmap().getWidth()*1.5f,0f);的意思就是在上述矩阵的左边再乘以下面的矩阵：</span></p>
396. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217126508k4V.gif"alt=""></span></p>
397. <p><spanstyle="font-size:13px">关于post是左乘这一点，我们在前面的理论部分曾经提及过，后面我们还会专门讨论这个问题。</span></p>
398. <p><spanstyle="font-size:13px"></span></p>
399. <p><spanstyle="font-size:13px">所以它实际上就是：</span></p>
400. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217126608wdT.gif"alt=""></span></p>
401. <p><spanstyle="font-size:13px">出去计算上的精度误差，我们可以看到我们计算出来的结果，和程序直接输出的结果是一致的。</span></p>
402. <p><spanstyle="font-size:13px"></span></p>
403. <p><spanstyle="font-size:13px">3.旋转(围绕坐标原点旋转，在加上两次平移，效果同2)</span></p>
404. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_132171250556xp.gif"alt=""></span></p>
405. <p><spanstyle="font-size:13px">根据第一部分中“二、旋转变换”里面关于围绕某点旋转的解释，不难知道：</span></p>
406. <p><spanstyle="font-size:13px">matrix.setRotate(45f,view.getImageBitmap().getWidth()/2f,view.getImageBitmap().getHeight()/2f);</span></p>
407. <p><spanstyle="font-size:13px">等价于</span></p>
408. <p><spanstyle="font-size:13px">matrix.setRotate(45f);</span></p>
409. <p><spanstyle="font-size:13px">matrix.preTranslate(-1f*view.getImageBitmap().getWidth()/2f,-1f*view.getImageBitmap().getHeight()/2f);</span></p>
410. <p><spanstyle="font-size:13px">matrix.postTranslate((<strong>float</strong>)view.getImageBitmap().getWidth()/2f,(<strong>float</strong>)view.getImageBitmap().getHeight()/2f);</span></p>
411. <p><spanstyle="font-size:13px"></span></p>
412. <p><spanstyle="font-size:13px">其中matrix.setRotate(45f)对应的矩阵是：</span></p>
413. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321712949GjN7.gif"alt=""></span></p>
414. <p><spanstyle="font-size:13px">matrix.preTranslate(-1f*view.getImageBitmap().getWidth()/2f,-1f*view.getImageBitmap().getHeight()/2f)对应的矩阵是：</span></p>
415. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321712956BNj8.gif"alt=""></span></p>
416. <p><spanstyle="font-size:13px">由于是preTranslate，是先乘，也就是右乘，即它应该出现在matrix.setRotate(45f)所对应矩阵的右侧。</span></p>
417. <p><spanstyle="font-size:13px"></span></p>
418. <p><spanstyle="font-size:13px">matrix.postTranslate((<strong>float</strong>)view.getImageBitmap().getWidth()/2f,(<strong>float</strong>)view.getImageBitmap().getHeight()/2f)对应的矩阵是：</span></p>
419. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321712963iNO1.gif"alt=""></span></p>
420. <p><spanstyle="font-size:13px">这次由于是postTranslate，是后乘，也就是左乘，即它应该出现在matrix.setRotate(45f)所对应矩阵的左侧。</span></p>
421. <p><spanstyle="font-size:13px"></span></p>
422. <p><spanstyle="font-size:13px">所以综合起来，</span></p>
423. <p><spanstyle="font-size:13px">matrix.setRotate(45f);</span></p>
424. <p><spanstyle="font-size:13px">matrix.preTranslate(-1f*view.getImageBitmap().getWidth()/2f,-1f*view.getImageBitmap().getHeight()/2f);</span></p>
425. <p><spanstyle="font-size:13px">matrix.postTranslate((<strong>float</strong>)view.getImageBitmap().getWidth()/2f,(<strong>float</strong>)view.getImageBitmap().getHeight()/2f);</span></p>
426. <p><spanstyle="font-size:13px">对应的矩阵就是：</span></p>
427. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713055HOOt.gif"alt=""></span></p>
428. <p><spanstyle="font-size:13px">这和下面这个矩阵(围绕图像中心顺时针旋转45度)其实是一样的：</span></p>
429. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713100VIOz.gif"alt=""></span></p>
430. <p><spanstyle="font-size:13px">因此，此处变换后的图像和2中变换后的图像时一样的。</span></p>
431. <p><spanstyle="font-size:13px"></span></p>
432. <p><spanstyle="font-size:13px">4.缩放变换</span></p>
433. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713185yKS7.gif"alt=""></span></p>
434. <p><spanstyle="font-size:13px">程序所输出的两个矩阵分别是：</span></p>
435. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217131941R24.gif"alt=""></span></p>
436. <p><spanstyle="font-size:13px">其中第二个矩阵，其实是下面两个矩阵相乘的结果：</span></p>
437. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713201VRxs.gif"alt=""></span></p>
438. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“三、缩放变换”和“一、平移变换”说法，自行验证结果。</span></p>
439. <p><spanstyle="font-size:13px"></span></p>
440. <p><spanstyle="font-size:13px">5.错切变换(水平错切)</span></p>
441. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_132171330766G0.gif"alt=""></span></p>
442. <p><spanstyle="font-size:13px">代码所输出的两个矩阵分别是：</span></p>
443. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713314Dk69.gif"alt=""></span></p>
444. <p><spanstyle="font-size:13px">其中，第二个矩阵其实是下面两个矩阵相乘的结果：</span></p>
445. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713322PeML.gif"alt=""></span></p>
446. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“四、错切变换”和“一、平移变换”的相关说法，自行验证结果。</span></p>
447. <p><spanstyle="font-size:13px"></span></p>
448. <p><spanstyle="font-size:13px">6.错切变换(垂直错切)</span></p>
449. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713502Akg2.gif"alt=""></span></p>
450. <p><spanstyle="font-size:13px">代码所输出的两个矩阵分别是：</span></p>
451. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713509Hz7p.gif"alt=""></span></p>
452. <p><spanstyle="font-size:13px">其中，第二个矩阵其实是下面两个矩阵相乘的结果：</span></p>
453. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713516TUvx.gif"alt=""></span></p>
454. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“四、错切变换”和“一、平移变换”的相关说法，自行验证结果。</span></p>
455. <p><spanstyle="font-size:13px"></span></p>
456. <p><spanstyle="font-size:13px">7.错切变换(水平+垂直错切)</span></p>
457. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321713655Qsij.gif"alt=""></span></p>
458. <p><spanstyle="font-size:13px">代码所输出的两个矩阵分别是：</span></p>
459. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217136824kKR.gif"alt=""></span></p>
460. <p><spanstyle="font-size:13px">其中，后者是下面两个矩阵相乘的结果：</span></p>
461. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217136931vl4.gif"alt=""></span></p>
462. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“四、错切变换”和“一、平移变换”的相关说法，自行验证结果。</span></p>
463. <p><spanstyle="font-size:13px"></span></p>
464. <p><spanstyle="font-size:13px">8.对称变换(水平对称)</span></p>
465. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217141232rJI.gif"alt=""></span></p>
466. <p><spanstyle="font-size:13px">代码所输出的两个各矩阵分别是：</span></p>
467. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714133P0ha.gif"alt=""></span></p>
468. <p><spanstyle="font-size:13px">其中，后者是下面两个矩阵相乘的结果：</span></p>
469. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217141417Bi3.gif"alt=""></span></p>
470. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“五、对称变换”和“一、平移变换”的相关说法，自行验证结果。</span></p>
471. <p><spanstyle="font-size:13px"></span></p>
472. <p><spanstyle="font-size:13px">9.对称变换(垂直对称)</span></p>
473. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714261NN3V.gif"alt=""></span></p>
474. <p><spanstyle="font-size:13px">代码所输出的两个矩阵分别是：</span></p>
475. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714269Kqs4.gif"alt=""></span></p>
476. <p><spanstyle="font-size:13px">其中，后者是下面两个矩阵相乘的结果：</span></p>
477. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714276ai2f.gif"alt=""></span></p>
478. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“五、对称变换”和“一、平移变换”的相关说法，自行验证结果。</span></p>
479. <p><spanstyle="font-size:13px"></span></p>
480. <p><spanstyle="font-size:13px">10.对称变换(对称轴为直线<em>y=x</em>)</span></p>
481. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217144950030.gif"alt=""></span></p>
482. <p><spanstyle="font-size:13px">代码所输出的两个矩阵分别是：</span></p>
483. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_13217145038hN8.gif"alt=""></span></p>
484. <p><spanstyle="font-size:13px">其中，后者是下面两个矩阵相乘的结果：</span></p>
485. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714509sBN4.gif"alt=""></span></p>
486. <p><spanstyle="font-size:13px">大家可以对照第一部分中的“五、对称变换”和“一、平移变换”的相关说法，自行验证结果。</span></p>
487. <p><spanstyle="font-size:13px"></span></p>
488. <p><spanstyle="font-size:13px">11.关于先乘和后乘的问题</span></p>
489. <p><spanstyle="font-size:13px">由于矩阵的乘法运算不满足交换律，我们在前面曾经多次提及先乘、后乘的问题，即先乘就是矩阵运算中右乘，后乘就是矩阵运算中的左乘。其实先乘、后乘的概念是针对变换操作的时间先后而言的，左乘、右乘是针对矩阵运算的左右位置而言的。以第一部分“二、旋转变换”中围绕某点旋转的情况为例：</span></p>
490. <p><spanstyle="font-size:13px"><imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714645396z.gif"alt=""></span></p>
491. <p><spanstyle="font-size:13px">越靠近原图像中像素的矩阵，越先乘，越远离原图像中像素的矩阵，越后乘。事实上，图像处理时，矩阵的运算是从右边往左边方向进行运算的。这就形成了越在右边的矩阵(右乘)，越先运算(先乘)，反之亦然。</span></p>
492. <p><spanstyle="font-size:13px"></span></p>
493. <p><spanstyle="font-size:13px">当然，在实际中，如果首先指定了一个matrix，比如我们先setRotate(<imgsrc="http://hi.csdn.net/attachment/201111/19/0_1321714654C9Xc.gif"alt="">)，即指定了上面变换矩阵中，中间的那个矩阵，那么后续的矩阵到底是pre还是post运算，都是相对这个中间矩阵而言的。</span></p>
494. <p><spanstyle="font-size:13px"></span></p>
495. <spanstyle="font-size:13px">所有这些，其实都是很自然的事情。</span>
496. <pre></pre>
497. <pre></pre>
498. <pre></pre>
499. <pre></pre>

第三部分 应用

在这一部分，我们会将前面两部分所了解到的内容和Android手势结合起来，利用各种不同的手势对图像进行平移、缩放和旋转，前面两项都是在实践中经常需要用到的功能，后一项据说苹果也是最近才加上的，而实际上在Android中，咱们通过自己的双手，也可以很轻松地实现之。

首先创建一个Android项目PatImageView，同时创建一个Activity：PatImageViewActivity。完成这一步后， 记得在AndroidManifest.xml中增加如下许可：

<uses-permissionandroid:name="android.permission.VIBRATE"/>

因为我们将要通过短按还是长按，来确定将图片到底是缩放还是旋转。

现在来创建一个ImageView的派生类：PatImageView，其代码(PatImageView.java)如下(2011-11-22 revised)：

[java] view plain copy

1. packagecom.pat.imageview;
3. importandroid.app.Service;
4. importandroid.content.Context;
5. importandroid.graphics.Matrix;
6. importandroid.graphics.PointF;
7. importandroid.os.Vibrator;
8. importandroid.util.FloatMath;
9. importandroid.view.GestureDetector;
10. importandroid.view.MotionEvent;
11. importandroid.view.View;
12. importandroid.widget.ImageView;
14. publicclassPatImageViewextendsImageView
15. {
16. privateMatrixmatrix;
17. privateMatrixsavedMatrix;
19. privatebooleanlong_touch=false;
20. privatestaticintNONE=0;
21. privatestaticintDRAG=1;//拖动
22. privatestaticintZOOM=2;//缩放
23. privatestaticintROTA=3;//旋转
24. privateintmode=NONE;
26. privatePointFstartPoint;
27. privatePointFmiddlePoint;
29. privatefloatoldDistance;
30. privatefloatoldAngle;
32. privateVibratorvibrator;
34. privateGestureDetectorgdetector;
36. publicPatImageView(finalContextcontext)
37. {
38. super(context);
40. matrix=newMatrix();
41. savedMatrix=newMatrix();
43. matrix.setTranslate(0f,0f);
44. setScaleType(ScaleType.MATRIX);
45. setImageMatrix(matrix);
47. startPoint=newPointF();
48. middlePoint=newPointF();
50. oldDistance=1f;
52. gdetector=newGestureDetector(context,newGestureDetector.OnGestureListener()
53. {
54. @Override
55. publicbooleanonSingleTapUp(MotionEvente)
56. {
57. returntrue;
58. }
60. @Override
61. publicvoidonShowPress(MotionEvente)
62. {
63. }
65. @Override
66. publicbooleanonScroll(MotionEvente1,MotionEvente2,floatdistanceX,floatdistanceY)
67. {
68. returntrue;
69. }
71. @Override
72. publicvoidonLongPress(MotionEvente)
73. {
74. long_touch=true;
75. vibrator=(Vibrator)context.getSystemService(Service.VIBRATOR_SERVICE);
76. //振动50ms，提示后续的操作将是旋转图片，而非缩放图片
77. vibrator.vibrate(50);
78. }
80. @Override
81. publicbooleanonFling(MotionEvente1,MotionEvente2,floatvelocityX,floatvelocityY)
82. {
83. returntrue;
84. }
86. @Override
87. publicbooleanonDown(MotionEvente)
88. {
89. returntrue;
90. }
91. });
93. setOnTouchListener(newOnTouchListener()
94. {
95. publicbooleanonTouch(Viewview,MotionEventevent)
96. {
97. switch(event.getAction()&MotionEvent.ACTION_MASK)
98. {
99. caseMotionEvent.ACTION_DOWN://第一个手指touch
100. savedMatrix.set(matrix);
101. startPoint.set(event.getX(),event.getY());
102. mode=DRAG;
103. long_touch=false;
104. break;
105. caseMotionEvent.ACTION_POINTER_DOWN://第二个手指touch
106. oldDistance=getDistance(event);//计算第二个手指touch时，两指之间的距离
107. oldAngle=getDegree(event);//计算第二个手指touch时，两指所形成的直线和x轴的角度
108. if(oldDistance>10f)
109. {
110. savedMatrix.set(matrix);
111. middlePoint=midPoint(event);
112. if(!long_touch)
113. {
114. mode=ZOOM;
115. }
116. else
117. {
118. mode=ROTA;
119. }
120. }
121. break;
122. caseMotionEvent.ACTION_UP:
123. mode=NONE;
124. break;
125. caseMotionEvent.ACTION_POINTER_UP:
126. mode=NONE;
127. break;
128. caseMotionEvent.ACTION_MOVE:
129. if(vibrator!=null)vibrator.cancel();
130. if(mode==DRAG)
131. {
132. matrix.set(savedMatrix);
133. matrix.postTranslate(event.getX()-startPoint.x,event.getY()-startPoint.y);
134. }
136. if(mode==ZOOM)
137. {
138. floatnewDistance=getDistance(event);
140. if(newDistance>10f)
141. {
142. matrix.set(savedMatrix);
143. floatscale=newDistance/oldDistance;
144. matrix.postScale(scale,scale,middlePoint.x,middlePoint.y);
145. }
146. }
148. if(mode==ROTA)
149. {
150. floatnewAngle=getDegree(event);
151. matrix.set(savedMatrix);
152. floatdegrees=newAngle-oldAngle;
153. matrix.postRotate(degrees,middlePoint.x,middlePoint.y);
154. }
155. break;
156. }
157. setImageMatrix(matrix);
158. invalidate();
159. gdetector.onTouchEvent(event);
160. returntrue;
161. }
162. });
163. }
165. //计算两个手指之间的距离
166. privatefloatgetDistance(MotionEventevent)
167. {
168. floatx=event.getX(0)-event.getX(1);
169. floaty=event.getY(0)-event.getY(1);
170. returnFloatMath.sqrt(x*x+y*y);
171. }
173. //计算两个手指所形成的直线和x轴的角度
174. privatefloatgetDegree(MotionEventevent)
175. {
176. return(float)(Math.atan((event.getY(1)-event.getY(0))/(event.getX(1)-event.getX(0)))*180f);
177. }
179. //计算两个手指之间，中间点的坐标
180. privatePointFmidPoint(MotionEventevent)
181. {
182. PointFpoint=newPointF();
183. floatx=event.getX(0)+event.getX(1);
184. floaty=event.getY(0)+event.getY(1);
185. point.set(x/2,y/2);
187. returnpoint;
188. }
189. }

下面完善PatImageViewActivity.java的代码，使之如下：

[java] view plain copy

1. packagecom.pat.imageview;
3. importandroid.app.Activity;
4. importandroid.graphics.Bitmap;
5. importandroid.graphics.BitmapFactory;
6. importandroid.os.Bundle;
7. importandroid.view.Window;
8. importandroid.view.WindowManager;
10. publicclassPatImageViewActivityextendsActivity
11. {
12. @Override
13. publicvoidonCreate(BundlesavedInstanceState)
14. {
15. super.onCreate(savedInstanceState);
17. requestWindowFeature(Window.FEATURE_NO_TITLE);
18. this.getWindow().setFlags(WindowManager.LayoutParams.FLAG_FULLSCREEN,
19. WindowManager.LayoutParams.FLAG_FULLSCREEN);
21. PatImageViewpiv=newPatImageView(this);
22. Bitmapbmp=BitmapFactory.decodeResource(getResources(),R.drawable.sophie);
24. piv.setImageBitmap(bmp);
26. setContentView(piv);
27. }
28. }