java 常用查找算法

最新推荐文章于 2024-09-01 10:45:37 发布

iteye_7401

最新推荐文章于 2024-09-01 10:45:37 发布

阅读量143

点赞数

分类专栏： java 数据结构 java 文章标签： java 数据结构与算法

本文链接：https://blog.csdn.net/iteye_7401/article/details/82541420

版权

java 同时被 2 个专栏收录

21 篇文章 0 订阅

订阅专栏

java 数据结构

4 篇文章 0 订阅

订阅专栏

1 二分查找/折半查找

思想：在有序数组中查找某一特定元素的搜索算法。搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜素过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。

时间复杂度：折半搜索每次把搜索区域减少一半，时间复杂度为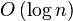 $O\left( \log n \right)$ 或log2(n)。（注意log2(n)和log(n)其实是同样的复杂度，因为它们之间仅仅差了一个常量系数而已）。（n代表集合中元素的个数）

空间复杂度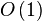： $O\left( 1 \right)$ 。虽以递归形式定义，但是尾递归，可改写为循环。

适用范围：优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

最多最少：元素有序时折半查找：最多+1次，最少1次；元素无序只能顺序查找：最多n次，最少1次

public class BinarySearch {
/**
* 二分查找算法，非递归
*
* @param srcArray 有序数组
* @param des 查找元素
* @return des的数组下标，没找到返回-1
*/
    public static int binarySearch(int[] srcArray, int des)
    {
        int low = 0;
        int high = srcArray.length-1;
        while(low <= high) 
        {
            int middle = (low + high)/2;
            if(des == srcArray[middle]) 
            {
                return middle;
            }
            else if(des <srcArray[middle]) 
            {
                high = middle - 1;
            }
            else
            {
                low = middle + 1;
            }
        }
        return -1;
    }
    public static void main(String[] args)
    {
        int[] src = new int[] {1, 3, 5, 7, 8, 9};
        System.out.println(binarySearch(src, 3));
    }
}

 //折半查找递归算法 
    //查询成功返回该对象的下标序号，失败时返回-1。 
    int BiSearch2(int r[],int low,int high,int k) 
    { 
        if(low>high) 
            return -1; 
        else 
        { 
            int mid=(low+high)/2; 
            if(r[mid]==k) 
                return mid; 
            else 
                if(r[mid]<k) 
                    return BiSearch2(r,mid+1,high,k); 
                else 
                    return BiSearch2(r,low,mid-1,k); 
 
        } 
    }

    public static void main(String[] args) { 
        int r[]={1,2,3,4,5}; 
        System.out.println(BiSearch2(r,1,5,5)); 
    }

参考：http://zh.wikipedia.org/wiki/%E6%8A%98%E5%8D%8A%E6%90%9C%E7%B4%A2%E7%AE%97%E6%B3%95

http://www.2cto.com/kf/201212/172713.html

2 二叉排序树

又称二叉查找(搜索)树(Binary Search Tree)。其定义为：二叉排序树或者是空树，或者是满足如下性质的二叉树：

①若它的左子树非空，则左子树上所有结点的值均小于根结点的值；
②若它的右子树非空，则右子树上所有结点的值均大于根结点的值；
③左、右子树本身又各是一棵二叉排序树。

　对于二叉排序树的查找，从根结点出发，当访问到树中某个结点时，如果该结点的关键字值等于给定的关键字值，就宣布查找成功。反之，如果该结点的关键字值大 ( 小 ) 于已给的关键字值，下一步就只需考虑查找右 ( 左 ) 子树了。

需要先实现二叉排序树，再进行查找

private TreeNode root = null;  
  /** 
     * insert: 将给定关键字插入到二叉查找树中 
     * @param key 给定关键字 
     */  
    public void insert(int key)  
    {  
        TreeNode parentNode = null;  
        TreeNode newNode = new TreeNode(key, null, null,null);  
        TreeNode pNode = root;  
        if (root == null) {  
            root = newNode;  
            return ;  
        }  
        while (pNode != null) {  
            parentNode = pNode;  
            if (key < pNode.key) {     
                pNode = pNode.leftChild;  
            }  
            else if (key > pNode.key) {  
                pNode = pNode.rightChild;  
            } else {  
                // 树中已存在匹配给定关键字的结点，则什么都不做直接返回                    
                return ;  
            }  
        }  
        if (key < parentNode.key) {  
            parentNode.leftChild = newNode;  
            newNode.parent = parentNode;  
        }  
        else {  
            parentNode.rightChild = newNode;  
            newNode.parent = parentNode;  
        }         
          
    }

 /** 
     * search: 在二叉查找树中查询给定关键字  
     * @param key 给定关键字 
     * @return 匹配给定关键字的树结点 
     */  
    public TreeNode search(int key)   
    {  
        TreeNode pNode = root;  
        while (pNode != null && pNode.key != key) {  
            if (key < pNode.key) {  
                pNode = pNode.leftChild;  
            }  
            else {  
                pNode = pNode.rightChild;  
            }  
        }  
        return pNode;  
    }

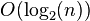最坏情况下，当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树，树的深度为 $n$ ，其平均查找长度为 $\frac{n+1}{2}$ （和顺序查找相同），最好的情况是二叉排序树的形态和折半查找的判定树相同，其平均查找长度和 $\log_2(n)$ 成正比（ $O(\log_2(n))$ ）

参考： http://blog.csdn.net/lovesqcc/article/details/6246615

http://zh.wikipedia.org/wiki/%E4%BA%8C%E5%85%83%E6%90%9C%E5%B0%8B%E6%A8%B9

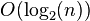3哈希

二分法平均查找效率是O(logn)，但是需要数组是排序的。如果没有排过序，就只好先用O（nlogn)的预处理为它排个序了。而且它的插入比较困难，经常需要移动整个数组，所以动态的情况下比较慢。

哈希查找理想的插入和查找效率是O(1)，但条件是需要找到一个良好的散列函数，使得分配较为平均。另外，哈希表需要较大的空间，至少要比O(n)大几倍，否则产生冲突的概率很高。

二叉排序树查找也是O(logn)的，关键是插入值时需要做一些处理使得它较为平衡（否则容易出现轻重的不平衡，查找效率最坏会降到O(n)）