圆排列问题

Ø给定n个大小不等的圆c1,c2,…,cn，现要将这n个圆排进一个矩形框中，且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。

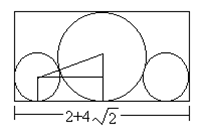
Ø例如，当n=3，且所给的3个圆的半径分别为1，1，2时，这3个圆的最小长度的圆排列如图所示。其最小长度为2+4√2。

void Circle::Backtrack(int t)

{

if (t>n) Compute();

else

for (int j = t; j <= n; j++) {

Swap(r[t], r[j]);

float centerx=Center(t);

if (centerx+r[t]+r[1]<min)

{//下界约束

x[t]=centerx;

Backtrack(t+1);}

Swap(r[t], r[j]);}

}

float Circle::Center(int t)

{// 计算当前所选择圆的圆心横坐标

float temp=0;

for (int j=1;j<t;j++) {

float valuex=x[j]+2.0*sqrt(r[t]*r[j]);

if (valuex>temp) temp=valuex;

}

return temp;

}

void Circle::Compute(void)

{// 计算当前圆排列的长度

float low=0,

high=0;

for (int i=1;i<=n;i++) {

if (x[i]-r[i]<low) low=x[i]-r[i];

if (x[i]+r[i]>high) high=x[i]+r[i];

}

if (high-low<min) min=high-low;

}

Ø上述算法尚有许多改进的余地。例如，象1,2,…,n-1,n和n,n-1, …,2,1这种互为镜像的排列具有相同的圆排列长度，只计算一个就够了，可减少约一半的计算量。

Ø另一方面，如果所给的n个圆中有k个圆有相同的半径，则这k个圆产生的k! 个完全相同的圆排列，只计算一个就够了。