分析时间复杂度

前言

算法是程序的灵魂，那么一段程序又是什么，想必大家都听说过这个概念吧~~程序=数据结构+算法，数据结构与算法是相辅相成，既有联系又有区别。

---

一、时间复杂度分析

1.1、概述

算法由控制结构和原操作构成，我们分析一个算法是撇开计算机的硬件和软件的这些因素，仅考虑算法本身的效率。算法的执行时间主要与问题规模有关。
我们取一段程序的渐进上界，作为一段程序的时间复杂度，且低阶项在决定渐进确界的时候可以忽略不记，例如：O(n²+n) = O(n²)。反之，紧凑下界也是类似。

1.2、时间复杂度示例

从上至下，时间复杂度依次递增，每次碰到一个时间复杂度高的算法，我们要尽量往低的优化。

简称	执行次数	时间复杂度
常数阶	6	O(1)
线性阶	6n+6	O(n)
平方阶	6n2+6n+6	O(n2)
对数阶	6log2n+6	O(logn)
nlogn阶	6nlog2n+6	O(nlogn)
立方阶	6n3+6n2+6n+6	O(n3)
指数阶	2n+6	O(2n)

二、数列求和

2.1、等差数列

首项为a₁,公差为d（d!=0）的数列a₁，a₁+d, a₁+2d, …, a₁+(n-1)d
通项公式：a_n=a₁+(n-1)d
前n项的和： S_n = n/2 [2a₁+(n-1)d] = n/2(a₁+a_n)

2.1、等比数列

首项为a₁,公比为q（q!=0）的数列a₁，a₁q, a₁q², …, a₁q^(n-1)
通项公式：a_n=q^n-1
前n项的和：
                  S_n = na₁，                        q=1
                  S_n = (a₁(1-qⁿ ) ) / (1-q) ， q!=1

2.3、常见数列前n项的和

2.4、数列类型的时间复杂度推导

程序代码：

#include <iostream>
using namespace std;
void solve(){
	int sum=0;
	for(int i=0;i<n;i++){
		for(int j=0;j<i;j++){
			for(int k=0;k<j;k++)
				sum++;
		}
	}
	return;
}

int main(int argc, char *argv[])
{
	solve();
	return 0;
}

时间复杂度分析：有些人能一眼看出这个程序的时间复杂度是多少，对，就是O(n³)，但是你能够写出如何推导的过程吗？下面我们就来推导下上面这段程序的时间复杂度吧！

时间复杂度推导：

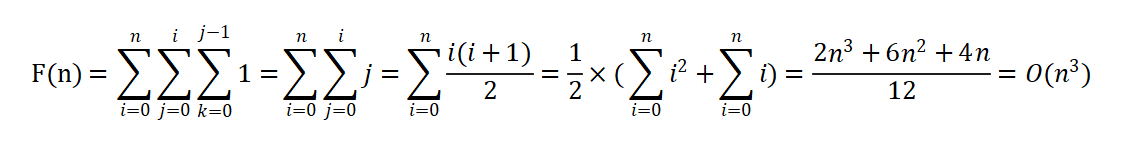
通过上述推导，我们得到时间复杂度为O(n³)

三、递推式计算：递归算法的分析

3.1、程序代码：

#include <iostream>
#include <vector>
using namespace std;

//归并排序采用分治的思想，先分后治
vector<int> mergesort(vector<int> before) {
	if (before.size() == 1)return before; //这是递归出口，二路分割到最后只剩一个元素
	vector<int>left, right, add_left_right;
	//先分
	for (int i = 0; i < before.size() / 2; i++) {
		left.push_back(before[i]);
	}
	for (int i = before.size() / 2; i < before.size(); i++) {
		right.push_back(before[i]);
	}
	//继续递归分割
	left = mergesort(left);
	right = mergesort(right);

	//后治
	int i = 0, j = 0;
	while (i < left.size() && j < right.size()) { //左右两块，进行比较排序
		if (left[i] < right[j]) {
			add_left_right.push_back(left[i]);
			i++;
		}
		else {
			add_left_right.push_back(right[j]);
			j++;
		}
	}
	if (i == left.size()) {   //左边排好，接着排右边剩下的数
		for (int k = j; k < right.size(); k++) {
			add_left_right.push_back(right[k]);
		}
	}
	if (j == right.size()) {
		for (int k = i; k < left.size(); k++) {
			add_left_right.push_back(left[k]);
		}
	}
	return add_left_right;
}

void solve() {
	int n;
	vector<int> my_array;
	while (cin >> n) {
		my_array.push_back(n);
	}
	my_array = mergesort(my_array);
	vector<int>::iterator iter;
	for ( iter = my_array.begin(); iter < my_array.end(); iter++) {
		cout << *iter << " ";
	}
	cout << endl;
}

int main() {
	solve();
	return 0;
}

3.2、直接推导法

3.2.1、时间复杂度分析：

递归算法是将大问题分解一个个小问题进行求解，分析递归算法的关键就是建立递推关系式，然后求解得到时间复杂度。
归并算法的递推关系式：

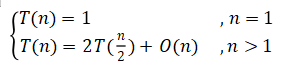
3.2.2、推导公式：

3.3、主方法

3.3.1、一般公式：

T（n）=aT(n/b)+f(n)

3.3.2、比较过程：

1. 函数n^log_ba比函数f(n)大，则T（n） = O（n^log_ba）
2. 函数n^log_ba比函数f(n)相等，则T（n） = O（n^log_balog₂ⁿ）
3. 函数n^log_ba比函数f(n)小，则T（n） = O（f(n)）

3.3.3推导例子：

如3.1的程序，递推公式为2（T(n/2)+n）
则n^log_ba=n^log₂2=n，f(n)=n;
得到：n^log₂2==f(n);
所以根据比较过程得到T(n)= nlog₂ⁿ

---

总结

算法是程序的灵魂，数据结构与算法是相辅相成，既有联系又有区别。学习好时间复杂度的分析尤为重要。

如有错误，敬请指正！