红黑树实现

于 2015-03-01 22:23:29 发布
阅读量421 收藏 1
点赞数
分类专栏： 数据结构 文章标签： 数据结构 源码 红黑树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/iylei/article/details/44007165
版权

  1.红黑树的由来

     红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数数据结构，典型的用途是实现关联数组。

它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。

红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除。

2.红黑树的性质

  红黑树首先是一颗二叉查找树，它的每个结点要么是红色，要么是黑色，它满足个性质：

 1，每个结点要么是红色，要么是黑色。
 2，根结点是黑色。
 3，叶子结点看作黑色结点，同时也被叫做黑哨兵。
 4，任何一条路径上不可能出现相邻两个红色结点，即每个红色结点都有两个黑色子结点。
 5，任何结点到其子孙结点所有路径上有相同数量的黑色结点。

3.红黑树的插入，当然每个结点初始为红色

   1，如果红黑树为空，即插入结点为根结点，把结点变为黑色即可。
   2，如果插入结点父结点为黑，直接插入。

3，如果插入结点的父结点为红色，则其祖父结点必为黑色，此时较为复杂。由其叔叔结点决定进一步操作。


3.1 当叔结点为红色，则把父结点，叔结点变为黑色，祖父结点变为红色。以祖父结点作为新结点向上进行平衡操作。


需要注意的是无论结点叔是祖父结点的左孩子还是右孩子，调整都一样。

3.2当叔结点是黑色时，则进行旋转操作，有以下情况：
 
情况1：
         

        


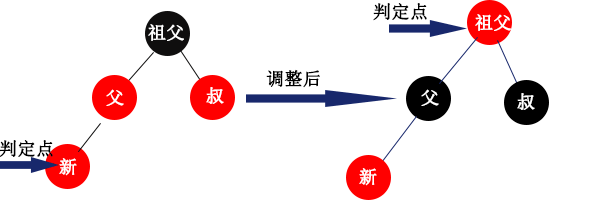
情况2：



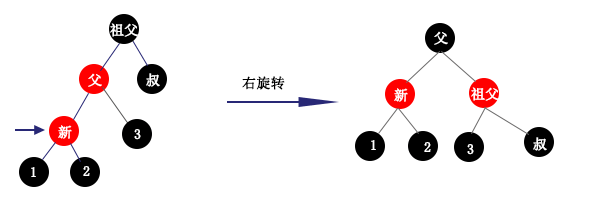
情况3：当父结点为祖父结点的左孩子，且新插入结点为父结点的左孩子时进行左旋转，和情况1类似，只是旋转方向不同而已。



情况4：当父结点为祖父结点的左孩子时，且新插入结点为父结点的右孩子时，先右旋转，后左旋，和情况2类似。


到此红黑树插入调整的各种情况介绍结束，其实插入并不难，但是红黑树的删除比AVL树复杂的多。


4，红黑树的删除

     红黑树的删除比较复杂，当然先把结点按照二叉搜索树方法删除，然后再调整。二叉搜索树的删除有复制删除和合并删除，复制删除较为重用。采用复制删除，结合红黑树的特点，有以下情况。

  情况1：真正删除的结点必定是只有一个红色孩子的结点或者是叶结点；

  情况2：如果真正删除的结点是 一个红色的结点，那么这个结点一定是叶子。

以下讨论删除的各种情况，当结点被标注为“旧”时表示真正被删除的结点，新结点表示删除后代替结点。


1，当红黑树只有一个结点时，即只有根结点，那么直接删除，完成。


2，当删除结点为红色时，直接删除，因为不影响红黑树的性质。


3，当真正删除结点有一个红色孩子，删除时把被删除点红色孩子变为黑色即可。

4，当删除结点为叶子且为黑色时，由于是黑色的叶结点，则必有兄弟结点，此时情况比较复杂，有以下情况。

 

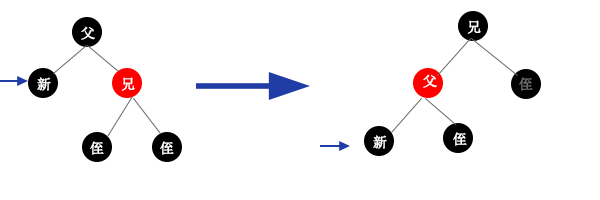
情况1：当被删除结点的兄弟为红色时，由于兄弟结点是红色，则父结点必为黑色，首先可以进行旋转操作后再进行调整。


当然，如果兄结点为右孩子，则进行右旋转，然后以新结点进行调整。从变化来看都是经过旋转后把兄弟结点变为黑色，父结点变为红色。


情况2：当被删除结点兄弟结点为黑色时，且父结点为红色时，此时直接把父结点变为黑色，兄弟结点变为红色




如果兄弟结点为右孩子，则一样，把父结点变为黑色，兄弟结点变为红色。


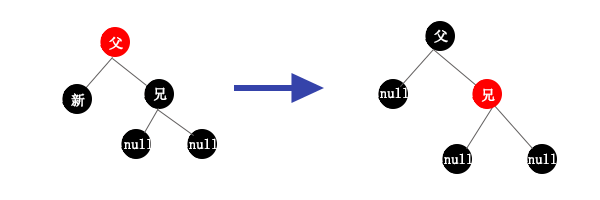
情况3：兄弟结点为黑色，父结点也为黑色，则把兄弟结点变为红色即可。


情况4：如果有红色的侄出现，则进行以下变化。


 4.4.1


4.4.2


4.4.3如果出现右兄右侄时则进行左旋，同时把兄弟结点变为父结点颜色，同时把父结点，侄子结点变为黑色。与4.4.1相似。


4.4.3如果出现右兄左侄，则先进行右旋，后进行左旋，同时把兄弟结点和父结点变为黑色，侄子结点变为与新结点的父结点相同的颜色。与4.4.2相似。


5 源码

#include<iostream>
#include<ctime>
using namespace std;
typedef  bool red;
#define RED 1
#define BLACK 0
template<class T>
class RB_tree_node
{
public:
	T data;
	RB_tree_node<T> *parent;
	RB_tree_node<T> *leftChild;
	RB_tree_node<T> *rightChild;
	red red_node;
	RB_tree_node();
	RB_tree_node(T item);
};
template<class T>
class RB_tree
{
private:
	RB_tree_node<T> *root;
public:
	RB_tree();
	~RB_tree();
	RB_tree_node<T>* search(T &data);
	void Insert(T data);
	void Delete(T data);
	void DeleteFixup(RB_tree_node<T> *old_node);
	void Inorder();
	void resverse(RB_tree_node<T> *node);
	void free(RB_tree_node<T> *t);
	void show(RB_tree_node<T> *rb)
	{
		cout << rb->data << " " << rb->red_node << endl;
	}
};
template<class T>
class stack
{
private:
	int maxSize;
	int top;
	T *atr;
public:
	stack(int szie = 0);
	~stack();
	bool IsEmpty();
	bool IsFull();
	bool pop(T& item);
	bool push(T&item);
	void clear();
	T GetTop();
};
template<class T>
stack<T>::stack(int size)
{
	maxSize = size;
	top = -1;
	atr = new T[maxSize];
}
template<class T>
stack<T>::~stack()
{
	delete[]atr;
}
template<class T>
bool stack<T>::IsEmpty()
{
	return top == -1;
}
template<class T>
bool stack<T>::IsFull()
{
	return top == maxSize - 1;
}
template<class T>
bool stack<T>::pop(T &item)
{
	if (top == -1)
	{
		cout << "error" << endl;
		return false;
	}

	else
	{
		item = atr[top--];
		return true;
	}
}
template<class T>
bool stack<T>::push(T &item)
{
	if (top == maxSize - 1)
	{
		cout << "error" << endl;
		return false;
	}

	else
	{
		atr[++top] = item;
		return true;
	}
}
template<class T>
T stack<T>::GetTop()
{
	return  atr[top];
}
template<class T>
RB_tree_node<T>::RB_tree_node()
{
	data = 0;
	leftChild = NULL;
	rightChild = NULL;
	parent = NULL;
	red_node = RED;
}
template<class T>
RB_tree_node<T>::RB_tree_node(T item)
{
	data = item;
	leftChild = NULL;
	rightChild = NULL;
	parent = NULL;
	red_node =RED;
}
template<class T>
RB_tree<T>::RB_tree()
{
	root = NULL;
}
template<class T>
RB_tree<T>::~RB_tree()
{
	free(root);
}
template<class T>
RB_tree_node<T>* RB_tree<T>::search(T &data)
{
	RB_tree_node<T> *p = root;
	while (p)
	{
		if (p->data == data)
			break;
		else
		{
			if (p->data > data)
				p = p->leftChild;
			else
			{
				p = p->rightChild;
			}
		}
	}
	return p;
}
template<class T>
void RB_tree<T>::Insert(T data)
{
	RB_tree_node<T> *rb_node = new RB_tree_node<T>(data),*pre=root,*current=root;
	if (root == NULL)
	{
		root = rb_node;
	}
	else
	{
		current = pre = root;
		while (current)
		{
			pre=current;
			if (current->data > data)
			{
				current= current->leftChild;
			}
			else
			{
				current = current->rightChild;
			}
		}
		if (data < pre->data)
		{
			pre->leftChild = rb_node;
			rb_node->parent = pre;
		}
		else
		{
			pre->rightChild = rb_node;
			rb_node->parent = pre;
		}
	}
	resverse(rb_node);
}
template<class T>
void RB_tree<T>::resverse(RB_tree_node<T>*node)
{
	RB_tree_node<T> *node_parent,*node_grend;
	while (1)
	{
		node_parent = node->parent;
		if (!node)
			break;
		else if (node_parent == NULL)
		{
			node->red_node = BLACK;
			break;
		}
		else if(node_parent&&node_parent->red_node==BLACK)
		{
			break;
		}
		else if (node_parent->red_node==RED)
		{
			node_grend = node_parent->parent;
			if (node_grend->leftChild == node_parent)
			{
				if (node_grend->rightChild&&node_grend->rightChild->red_node == RED)
				{
					node_grend->red_node = RED;
					node_parent->red_node = BLACK;
					node_grend->rightChild->red_node = BLACK;
					node = node_grend;
				}
				else
				{
					if (node_parent->rightChild == node)
					{
						if (node->leftChild)
						{
							node->leftChild->parent = node_parent;
							node_parent->rightChild = node->leftChild;
						}
						else
						{
							node_parent->rightChild = NULL;
						}
						node->parent = node_parent->parent;
						node_parent->parent->leftChild = node;
						node->leftChild = node_parent;
						node_parent->parent = node;
						node_parent = node->parent;
						node_grend = node_parent->parent;
					}
					else
					{
						node_grend = node_grend->parent;
						node_parent = node_parent->parent;
						node = node->parent;
					}
					if (node->rightChild)
					{
						node->rightChild->parent = node_parent;
						node_parent->leftChild = node->rightChild;
					}
					else
					{
						node_parent->leftChild = NULL;
					}
					if (node_grend)
					{
						if (node_grend->leftChild == node_parent)
						{
                            node_grend->leftChild = node;
						}
						else
						{
							node_grend->rightChild = node;
						}
						node->parent = node_grend;
						
					}
					else
					{
                        node->parent = NULL;
						root = node;
					}
					
					node->rightChild = node_parent;
					node_parent->parent = node;
					node->red_node = BLACK;
					node->rightChild->red_node = RED;
					break;
				}
				
			}
			else
			{
				if (node_grend->leftChild&&node_grend->leftChild->red_node == RED)
				{
					node_grend->red_node = RED;
					node_parent->red_node = BLACK;
					node_grend->leftChild->red_node = BLACK;
					node = node_grend;
				}
				else
				{
					if (node->parent->leftChild == node)
					{
						if (node->rightChild)
						{
							node->rightChild->parent = node_parent;
							node_parent->leftChild = node->rightChild;
						}
						else
						{
							node_parent->leftChild = NULL;
						}
						node->parent = node_parent->parent;
						node->parent->rightChild = node;
						node_parent->parent = node;
						node->rightChild = node_parent;
						node_parent = node->parent;
						node_grend = node_parent->parent;
					}
					else
					{
						node_grend = node_grend->parent;
						node_parent = node_parent->parent;
						node = node->parent;
					}
					if (node->leftChild)
					{
						node->leftChild->parent = node_parent;
						node_parent->rightChild = node->leftChild;
					}
					else
					{
						node_parent->rightChild = NULL;
					}
					if (node_grend)
					{
						if (node_grend->rightChild == node_parent)
						{
							node_grend->rightChild = node;
                         }                     
						else
						{
							node_grend->leftChild = node;
						}
						node->parent = node_grend;
						
					}
					else
					{
	                   node->parent = NULL;
					   root = node;

					}
					node_parent->parent = node;
					node->leftChild = node_parent;
					node->red_node = BLACK;
					node->leftChild->red_node = RED;
					break;
				}
			}
		}
	}
}
template<class T>
void RB_tree<T>::free(RB_tree_node<T> *t)
{
	if (t)
	{
		free(t->leftChild);
		free(t->rightChild);
		delete t;
	}
}
template<class T>
void RB_tree<T>::Inorder()
{
	stack<RB_tree_node<T> *> s(30);
	RB_tree_node<T> *ptr = root;
	while (!s.IsEmpty() || ptr)
	{
		if (ptr)
		{
			s.push(ptr);
			ptr = ptr->leftChild;
		}
		else
		{
			s.pop(ptr);
			cout << "(" << ptr->data << ",";
			if (ptr->red_node)
				cout << "red" << ")" << endl;
			else
				cout << "black" << ")" << endl;
			ptr = ptr->rightChild;
		}
	}
}
template<class T>
void RB_tree<T>::Delete(T data)
{
	RB_tree_node<T> *ptr = root,*current=root,*pre=root,*ptr_pre;
	while (current)
	{
		
		if (current->data == data)
			break;
		else if (current->data > data)
		{
			pre = current;
			current = current->leftChild;
		}
		else
		{
			pre = current;
			current = current->rightChild;
		}
	}
	if (!current->leftChild&&!current->rightChild)
	{
		if (pre == current)
		{
			root = NULL;
		}
		else
		{
			if (pre->leftChild == current)
				pre->leftChild = NULL;
			else
			{
				pre->rightChild = NULL;
			}
		}
		DeleteFixup(current);
	}
	else if (current->leftChild&&!current->rightChild)
	{
		if (pre == current)
		{
			root = current->leftChild;
			root->parent = NULL;
		}
		else
		{
			if (pre->leftChild == current)
			{
				pre->leftChild = current->leftChild;
				current->leftChild->parent = pre;
			}
			else
			{
				pre->rightChild = current->leftChild;
				current->leftChild->parent = pre;
			}

		}
		DeleteFixup(current);
	}
	else if (current->rightChild&&!current->leftChild)
	{
		if (pre == current)
		{
			root = current->rightChild;
			root->parent = NULL;
		}
		else
		{
			if (pre->leftChild == current)
			{
				pre->leftChild = current->rightChild;
				current->rightChild->parent = pre;
			}
			else
			{
				pre->rightChild = current->rightChild;
				current->rightChild->parent = pre;
			}
		}
		DeleteFixup(current);
	}
	else if (current->leftChild&¤t->rightChild)
	{
		ptr_pre = ptr = current->rightChild;
		while (ptr->leftChild)
		{
			ptr_pre = ptr;
			ptr = ptr->leftChild;
		}
		if (ptr == ptr_pre)
		{
			current->data = ptr->data;
			current->rightChild = ptr->rightChild;
			if (ptr->rightChild)
			{
				ptr->rightChild->parent = current;
			}
		}
		else
		{
			current->data = ptr->data;
			ptr_pre->leftChild = ptr->rightChild;
			if (ptr->rightChild)
			{
				ptr->rightChild->parent = ptr_pre;
			}
		}
		DeleteFixup(ptr);
	}
}
template<class T>
void RB_tree<T>::DeleteFixup(RB_tree_node<T> *old_node)
{
	RB_tree_node<T> *old_node_parent,*old_node_grend,*old_node_brother;
	while (1)
	{
		if (old_node->red_node==RED)
		{
			break;
		}
		else if (old_node->leftChild&&old_node->leftChild->red_node==RED||old_node->rightChild&&old_node->rightChild->red_node==RED)
		{
			if (old_node->leftChild)
			{
				old_node->leftChild->red_node = BLACK;
			}
			else
			{
				old_node->rightChild->red_node = BLACK;
			}
			break;
		}
		else
		{
			old_node_parent = old_node->parent;//parent
			old_node_grend = old_node_parent->parent;//grandfather
			if (old_node->parent == NULL&&!old_node->leftChild&&!old_node->rightChild)//删除仅有根节点的树；
			{
				break;
			}
		   if (old_node_parent->rightChild)
			{
				old_node_brother = old_node_parent->rightChild;
				if (old_node_parent->rightChild->red_node == RED)
				{
					old_node_parent->red_node = RED;
					old_node_brother->red_node = BLACK;
					if (old_node_brother->leftChild)
					{
						old_node_brother->leftChild->parent = old_node_parent;
						old_node_parent->rightChild = old_node_brother->leftChild;
					}
					else
					{
						old_node_parent->rightChild = NULL;
					}
					if (old_node_grend)
					{
						old_node_brother->parent = old_node_grend;
						if (old_node_grend->leftChild == old_node_parent)
						{
							old_node_grend->leftChild = old_node_brother;
						}
						else
						{
							old_node_grend->rightChild = old_node_brother;
						}
					}
					else
					{
						root = old_node_brother;
						old_node_brother->parent = NULL;
					}
					old_node_parent->parent = old_node_brother;
					old_node_brother->leftChild = old_node_parent;
				}
				else if (old_node->parent->rightChild->red_node==BLACK)
				{
					bool red_parent = old_node_parent->red_node == RED,
						b_brother_l = old_node_brother->leftChild && (old_node_brother->leftChild->red_node == BLACK),
						b_brother_r = old_node_brother->rightChild && (old_node_brother->rightChild->red_node == BLACK),
						null_brother_s = !old_node_brother->leftChild&&!old_node_brother->rightChild;
					if (red_parent && (null_brother_s || (b_brother_l&&b_brother_r)))
					{
						old_node->parent->red_node = BLACK;
						old_node_brother->red_node = RED;
						break;
					}
					else if (!red_parent && (null_brother_s ||(b_brother_l&&b_brother_r)))
					{
						old_node_brother->red_node = RED;
						break;
					}
					else if (old_node_brother->rightChild&&old_node_brother->rightChild->red_node == RED)
					{
						old_node_brother->red_node = old_node_parent->red_node;
						old_node_parent->red_node = BLACK;
						old_node_brother->rightChild->red_node =BLACK;
						old_node_parent = old_node->parent;
						old_node_grend = old_node_parent->parent;
						if (old_node_brother->leftChild)
						{
							old_node_brother->leftChild->parent= old_node_parent;
							old_node_parent->rightChild = old_node_brother->leftChild;
						}
						else
						{
							old_node_parent->rightChild = NULL;
						}
						
						if (old_node_grend)
						{
							old_node_brother->parent = old_node_grend;
							if (old_node_grend->leftChild==old_node_parent)
							{
								old_node_grend->leftChild = old_node_brother;
							}
							else
							{
								old_node_grend->rightChild = old_node_brother;
							}
						}
						else
						{
							root = old_node_brother;
							old_node_brother->parent = NULL;
						}
						old_node_parent->parent = old_node_brother;
						old_node_brother->leftChild = old_node_parent;
						break;
					}
					else if (old_node_brother->leftChild&&old_node_brother->leftChild->red_node == RED)
					{
						old_node_brother->leftChild->red_node = old_node_parent->red_node;
						old_node_parent->red_node = BLACK;
						old_node_brother->leftChild->parent = old_node_parent;
						old_node_parent->rightChild = old_node_brother->leftChild;
						if (old_node_brother->leftChild->rightChild)
						{
							old_node_brother->leftChild->rightChild->parent = old_node_brother;
							old_node_brother->leftChild = old_node_brother->leftChild->rightChild;
						}
						else
						{
							old_node_brother->leftChild = NULL;
						}
						old_node_brother->parent = old_node_parent->rightChild;
						old_node_parent->rightChild->rightChild = old_node_brother;
						old_node_brother = old_node_parent->rightChild;
						old_node_grend = old_node_parent->parent;
						if (old_node_brother->leftChild)
						{
							old_node_brother->leftChild->parent = old_node_parent;
							old_node_parent->rightChild = old_node_brother->leftChild;
						}
						else
						{
							old_node_parent->rightChild = NULL;
						}
						if (old_node_grend)
						{
							old_node_brother->parent = old_node_grend;
							if (old_node_grend->rightChild == old_node_parent)
							{
								old_node_grend->rightChild = old_node_brother;
							}
							else
							{
								old_node_grend->leftChild = old_node_brother;
							}
						}
						else
						{
							root = old_node_brother;
							old_node_brother->parent = NULL;
						}
						old_node_parent->parent = old_node_brother;
						old_node_brother->leftChild = old_node_parent;
						break;
					}
				}
            }
			else
			{
				old_node_brother = old_node_parent->leftChild;
				if (old_node_brother->red_node == RED)
				{
					old_node_brother->red_node = BLACK;
					old_node_parent->red_node = RED;
					if (old_node_brother->rightChild)
					{
						old_node_brother->rightChild->parent = old_node_parent;
						old_node_parent->leftChild = old_node_brother->rightChild;
					}
					else
					{
						old_node_parent->leftChild = NULL;
					}
					if (old_node_grend)
					{
						old_node_brother->parent = old_node_grend;
						if (old_node_grend->leftChild == old_node_parent)
						{
							old_node_grend->leftChild = old_node_brother;
						}
						else
						{
							old_node_grend->rightChild = old_node_brother;
						}
					}
					else
					{
						root = old_node_brother;
						old_node_brother->parent = NULL;
					}
					old_node_parent->parent = old_node_brother;
					old_node_brother->rightChild = old_node_parent;
				}
				else if (old_node_parent->leftChild->red_node == BLACK)
				{
					bool red_p = old_node_parent->red_node == RED,
						b_bro_r = old_node_brother->leftChild&&old_node_brother->leftChild->red_node == BLACK,
						b_bro_l = old_node_brother->rightChild&&old_node_brother->rightChild->red_node == BLACK,
						null_node = !old_node_brother->rightChild&&!old_node_brother->leftChild;
					if (red_p && (null_node || (b_bro_l&&b_bro_r)))
					{
						old_node_parent->red_node = BLACK;
						old_node_brother->red_node = RED;
						break;
					}
					else if (!red_p && (null_node || (b_bro_l&&b_bro_r)))
					{
						old_node_brother->red_node = RED;
						break;
					}
					else if (old_node_brother->leftChild&&old_node_brother->leftChild->red_node == RED)
					{
						old_node_brother->red_node = old_node_parent->red_node;
						old_node_parent->red_node = BLACK;
						old_node_brother->leftChild->red_node = BLACK;
						if (old_node_brother->rightChild)
						{
							old_node_brother->rightChild->parent = old_node_parent;
							old_node_parent->leftChild = old_node_brother->rightChild;
						}
						else
						{
							old_node_parent->leftChild = NULL;
						}
						if (old_node_grend)
						{
							old_node_brother->parent = old_node_grend;
							if (old_node_grend->leftChild == old_node_parent)
							{
								old_node_grend->leftChild = old_node_brother;
							}
							else
							{
								old_node_grend->rightChild = old_node_brother;
							}
							
						}
						else
						{
							root = old_node_brother;
							old_node_brother->parent = NULL;
						}
						old_node_parent->parent = old_node_brother;
						old_node_brother->rightChild = old_node_parent;
						break;
					}
					else if (old_node_brother->rightChild&&old_node_brother->rightChild->red_node == RED)
					{ 
						old_node_brother->rightChild->red_node = old_node_parent->red_node;
						old_node->parent->red_node = BLACK;
						old_node_brother->rightChild->parent = old_node_parent;
						old_node_parent->leftChild = old_node_brother->rightChild;
						if (old_node_brother->rightChild->leftChild)
						{
							old_node_brother->rightChild->leftChild->parent = old_node_brother;
							old_node_brother->rightChild = old_node_brother->rightChild;
						}
						else
						{
							old_node_brother->rightChild = NULL;
						}
						old_node_brother->parent = old_node_parent->leftChild;
						old_node_parent->leftChild->leftChild = old_node_brother;
						old_node_parent = old_node->parent;
						old_node_grend = old_node_parent->parent;
						old_node_brother = old_node_parent->leftChild;
						if (old_node_brother->rightChild)
						{
							old_node_brother->rightChild->parent = old_node_parent;
							old_node_parent->leftChild = old_node_brother->rightChild;
						}
						else
						{
							old_node_parent->leftChild = NULL;
						}
						if (old_node_grend)
						{
							old_node_brother->parent = old_node_grend;
							if (old_node_grend->leftChild == old_node_parent)
							{
								old_node_grend->leftChild = old_node_brother;
							}
							else
							{
								old_node_grend->rightChild = old_node_brother;
							}
						}
						else
						{
							root = old_node_brother;
							old_node_brother->parent = NULL;
						}
						old_node_parent->parent = old_node_brother;
						old_node_brother->rightChild = old_node_parent;
						break;
					}
				}
			}
		}
	}
	delete old_node;
}


iylei
关注
专栏目录
简易STL实现 | 红黑树的实现
AsherGu的博客
09-25 977
原理：节点结构，插入操作，删除操作；代码实现：旋转，插入结点和插入修正；删除结点和删除修正；与标准库的差异
红黑树的实现
tunyue456的专栏
04-11 368
红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。 红黑树的五条性质：（特别重要） 1.节点是红色或黑色 2.根节点是黑色 3. 每个叶节点（NIL节点，空节点）是黑色的，又称为外节点 4.如果一个节点是红色的，则他的两个子节点都是黑色的 5.对每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的
红黑树实现源码
07-22
在提供的“红黑树.txt”文件中，可能包含了红黑树的具体源代码实现，可以详细阅读理解其工作原理。 总结来说，红黑树是一种高效且实用的数据结构，它的核心在于通过颜色属性和相应的调整策略来保持树的平衡，从而在...
C++红黑树实现过程
09-15
在C++中实现红黑树，需要理解并遵循红黑树的五个性质： 1. 每个节点要么是红色，要么是黑色。 2. 根节点是黑色。 3. 所有叶子节点（NIL或空节点）是黑色。 4. 如果一个节点是红色，则它的两个子节点都是黑色。 5. ...
红黑树实现java代码
11-01
红黑树实现java代码，供大家参考，具体详解请参见我的博客http://blog.csdn.net/clamclam/article/details/49545477
自研红黑树实现与代码详解
"这篇资源是作者自己编写的红黑树实现代码，基于《算法导论》（通常称为“黑书”）中的算法。代码已经能够正常工作，包含了一个`rb_tree`类，提供了插入、查找、获取最小值、后继节点等功能。" 红黑树是一种自平衡...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值