第一个nim积题目。nim积与nim和够成一个正整数域上的群。nim积用⊗表示,nim和用⊕表示。
和乘法类似:
x⊗1=1⊗x=x
y⊗0=0
(x⊗y)⊗z=x⊗(y⊗z)
⊕是异或运算。⊗的运算法则定义为:
1.The nimber product of distinct Fermat 2-powers (numbers of the form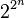 ) is equal to their ordinary product
) is equal to their ordinary product
2.The nimber square of a Fermat 2-power x is equal to 3 x/2 as evaluated under the ordinary multiplication of natural numbers.
这是维基百科上的定义,Fermat 2-powers前几个数是:2,4,16,256 ...
(1)对任意的x如果不是2的幂形式,就要把它化为二进制和的形式如:3=2+1,同样y也这么处理。利用分配率,可以得到logn个2^a⊗2^b相加的式子.
(2)再定义个函数来处理2的幂相乘的情况,将2^a化成Fermat 2-power相乘的形式,把2^a和2^b中不同的相直接相乘,而相同的项根据定义2,该项乘3/2.这样得到了一些一般的数,在调用(1)中的函数。
可以看到这两个函数是相互嵌套这的。
和乘法类似:
x⊗1=1⊗x=x
y⊗0=0
(x⊗y)⊗z=x⊗(y⊗z)
⊕是异或运算。⊗的运算法则定义为:
1.The nimber product of distinct Fermat 2-powers (numbers of the form
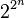 ) is equal to their ordinary product
) is equal to their ordinary product
2.The nimber square of a Fermat 2-power x is equal to 3 x/2 as evaluated under the ordinary multiplication of natural numbers.
这是维基百科上的定义,Fermat 2-powers前几个数是:2,4,16,256 ...
(1)对任意的x如果不是2的幂形式,就要把它化为二进制和的形式如:3=2+1,同样y也这么处理。利用分配率,可以得到logn个2^a⊗2^b相加的式子.
(2)再定义个函数来处理2的幂相乘的情况,将2^a化成Fermat 2-power相乘的形式,把2^a和2^b中不同的相直接相乘,而相同的项根据定义2,该项乘3/2.这样得到了一些一般的数,在调用(1)中的函数。
可以看到这两个函数是相互嵌套这的。
























 437
437

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








