【DP+预处理|最长连续子序列】HDU-1506 Largest Rectangle in a Histogram

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Problem Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

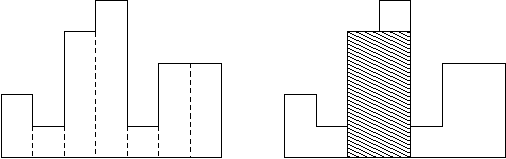
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

 

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

 

Sample Input

  
  

   
   7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
  
  

 

Sample Output

  
  

   
   8
4000
  
  

 

————————————————————————————————————————————————————————

题意：给出靠在一起的一列宽度为1的矩形。高度不同。找出这样一个子矩阵，使得它的面积最大。

思路：这儿有单调栈的做法：http://blog.csdn.net/j_sure/article/details/21103067

现在考虑DP的做法。

这类题目考的是预处理技巧。如果你枚举起点终点，O(n^2)超时，所以就必须通过预处理将复杂度降到O(n)。

就像是前缀和那样，我们设两个数组，l[ ]和r[ ]。来记录每个矩形左边最远能够到达的地方以及右边。

称之为左边界、右边界。

其实前缀和就是记录每个点的左边界为0，右边界为自身，是一种特殊的预处理。

现在有两个边界，并且边界是需要满足一定条件的。（即左边矩形高度不能比它低，右边同理，看题目图）

利用迭代法

采用旧值更新出新值，循环往复直到新值被确定。

说白了就是：每个点的起始左边界为自身，如果它左边界前面那个数tmp比它大，那么它的左边界变为tmp的左边界。

为什么还要确定右边界呢？自己思考。

接下来就是for一遍求max的事儿了。

P.S. 发现一件有趣的事情，DP法如果不使用%I64d而是使用%lld的话，在HDU-1506得到TLE，在POJ-2559得到TLE

单调栈法如果这样，HDU得到WA，POJ得到AC。总之使用%I64d就一定都AC。

代码如下：

/**
 * ID: j.sure.1
 * PROG:
 * LANG: C++
 */
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <map>
#include <set>
#include <string>
#include <climits>
#include <iostream>
#define For(i, x, y) for(int i=x; i<=y; i++)
#define For_(i, x, y) for(int i=x; i>=y; i--)
#define Mem(f, x) memset(f, x, sizeof(f))
#define Sca(x) scanf("%d", &x)
#define Pri(x) printf("%d\n", x)
#define LL long long
using namespace std;
const int INF = 0x3f3f3f3f;
/****************************************/
const int N = 111111;
int n;
LL a[N];
int l[N], r[N];

int main()
{
#ifdef J_Sure
    //freopen("000.in", "r", stdin);
    //freopen("999.out", "w", stdout);
#endif
    while(Sca(n), n) {
        For(i, 1, n) {
            scanf("%I64d", &a[i]);
            l[i] = r[i] = i;
        }
        a[0] = -1; a[n+1] = -1;
        //记录每个点左边最远到达谁
        For(i, 1, n) {
            while(a[i] <= a[l[i]-1]) {
                l[i] = l[l[i]-1];
            }//如果当前值比它左边界再左边一格的数小，那么更新它的左边界为左边界再左边一格的数的左边界
        }//This is called 迭代
        For_(i, n, 1) {
            while(a[i] <= a[r[i]+1]) {
                r[i] = r[r[i]+1];
            }
        }
        LL best = 0;
        For(i, 1, n) {
            LL cur = (r[i] - l[i] + 1) * a[i];
            best = max(best, cur);
        }
        printf("%I64d\n", best);
    }
    return 0;
}