UVa 11234 - Expressions

【题译】

通常两个操作数之间写入一个操作符可以组成算术表达式（又称中缀表达）。例如 (x+y)*(z-w) 就是一个基于中缀表达的表达式。然而，在编程方面，用后缀表达的表达式求值起来则要容易得多（又称逆波兰式）。在后缀表达上，一个表达式中的操作符往往被写在操作数的后面。例如， xy+zw-* 就是刚才的算术表达式用后缀表达的结果。值得注意的是，后缀表达不含括号。

为了求出一个后缀表达式的值，栈就是一个解决的方法。栈是一种数据结构，支持以下两种操作：

1.push：可将一个数字推入栈顶。

2.pop：可将位于栈顶的数字从中弹出。

在求值过程中，我们从左到右遍历后缀表达式。如果我们遇到操作数，就将其推入栈顶。如果我们遇到操作符，从栈中依次弹出两个操作数，针对这两个操作数和这个操作符进行运算，所得到的结果压入栈顶。当我们遇到操作符 o 的时候，下面这个伪代码就很好地说明了如何处理这个情况。

a:=pop();

b:=pop();

push(b, o, a);

这个后缀表达式的最终结果将是唯一一个留在栈中的操作数。

现在我们不用栈，而用队列来操作。队列也有push和pop两个操作，但它们的含义不同：

1.push：可将一个数字推入队尾。

2.pop：可将位于队头的数字从中弹出。

那我们是否可以重写后缀表达式，使得重写后的表达式通过队列操作的值与原先后缀表达式用栈操作的值一致呢？

（注：针对新表达式，用队列操作时，也是从左到右遍历，在遇到操作数进行push操作，遇到操作符进行pop操作）

【思路】

题目所给的输入是后缀表达式，用栈顺序遍历即可解决，但是现在题目要求给出队列对应的表达式，那么可以回想栈和队列的特点。后缀表达式可对应二叉树的后缀遍历，也就是说，输入可以转为一颗代表表达式的二叉树。如下图举例：

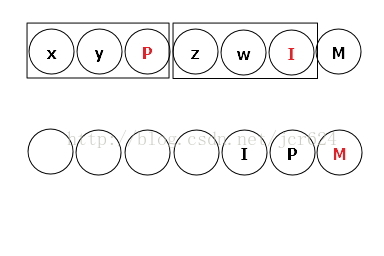
这棵树的中序遍历正好对应了中缀表达式 (xPy)M(zIw) ，大写字母为二叉树的非叶子结点，小写字母为二叉树的叶子节点。其后序遍历对应了后缀表达式 xyPzwIM，为题目中的第一个样例输入。

而队列与二叉树的共同点就是层次遍历，从这个角度出发，我们可以发现，由二叉树最深一层的叶子结点开始进行逆向层次遍历，所得到的结果就是我们要的答案，即表达式wzyxIPM。

考虑到建树还是比较麻烦的事情（本人比较懒-_-），需跳过建树的环节，模拟其遍历过程即可，针对第一个样例，过程如下：

根据原表达式字符串，生成一个与之长度相等的新串。由于旧串为二叉树的后序遍历，最后一个结点必定为二叉树树根，将其放入到新串末尾。

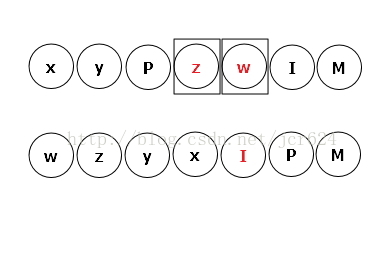
观察新串的当前结点，在后续遍历中找寻该结点的左、右子树，并找到左右子树的树根结点M。由于二叉树基于表达式生成，树中不包含度为1的结点，则 叶子结点数:=非叶子结点数+1 ，那么一颗完整的子树中 小写字母数:=大写字母数+1 ，根据这个规律去划分当前观察结点M的左右子树，下图左框部分为树根的左子树，右框为树根的右子树。框中的红色结点为子树的树根。

结点加入新串的规则是，先加入左子树的树根，再加入右子树树根，沿右向左放置。

新串中M结点观察完毕，再观察下一个结点P，找到P在旧串中的位置。

一直重复以上的过程，直到新串中所有结点观察完毕。

加入结点到新串中。

再观察下一个结点I，重复以上过程。

再观察下一个结点x，由于它是小写字母，为叶子结点，故不寻找子树，跳过，接着在新串中观察结点y。在该例中，x、y、z、w皆为叶子结点，遍历观察结束。

最终，输出新串即可。

【代码】

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <stack>
#include <queue>
#include <vector>
#include <list>
#include <set>
#include <algorithm>

#define loop_add(i, x1, x2) for (int i = (x1); i <= (x2); i ++)
#define loop_dec(i, x1, x2) for (int i = (x1); i >= (x2); i --)
#define	GetMax(a, b) ((a) > (b))? (a) : (b);
#define	GetMin(a, b) ((a) < (b))? (a) : (b);
#define EPS 1e-9
using namespace std;


// 给定新串中的一个结点位置和旧串，返回该结点左右子树树根在旧串的位置
void findLRroot(int &l, int &r, char* x, int cur) {
	l = r = 0;
	int upper = 0; // 大写字母计数
	int lower = 0; // 小写字母计数
	
	loop_dec(i, cur-1, 0) { // 旧串从右向左遍历寻找
		if (x[i] >= 'A' && x[i] <= 'Z')
			upper ++;
		else
			lower ++;
		
		if (upper+1 == lower) { // 找到符合条件的位置，可以限定右子树部分
			r = i+upper+lower-1; // 右子树树根的位置
			cur = i;
			break;
		}
	}

	upper = lower = 0;
	loop_dec(i, cur-1, 0) {
		if (x[i] >= 'A' && x[i] <= 'Z')
			upper ++;
		else
			lower ++;
		
		if (upper+1 == lower) { // 找到符合条件的位置，可以限定左子树部分
			l = i+upper+lower-1;// 左子树树根的位置
			break;
		}
	}
}


int main() {
	const int MAXN = 10010;
	char str[MAXN]; // 旧串
	char ans[MAXN]; // 新串

	int index[MAXN];// index[i]: 新串中下标为i的元素可在旧串下标index[i]处找到

	int T;
	int l, r; // 左、右子树的树根在旧串中的位置
	int len; // 旧串长度
	int queue; // 新串中新加入结点的位置

	scanf("%d", &T);
	while (T --) {
		scanf("%s", str);
		len = strlen(str);

		queue = len-1;
		ans[len] = '\0';

		if (len > 0) {
			ans[queue] = str[len-1];
			index[queue] = len-1;
			loop_dec(i, len-1, 0) {
				if (ans[i] >= 'A' && ans[i] <= 'Z') {
					findLRroot(l, r, str, index[i]);
					
					ans[-- queue] = str[l];
					index[queue] = l;

					ans[-- queue] = str[r];
					index[queue] = r;
				}
			}
			printf("%s\n", ans);
		}
		else {
			printf("\n");		
		}

	}
	return 0;
}