分治法的原理
讨论问题时,先来了解一下什么是分治法。
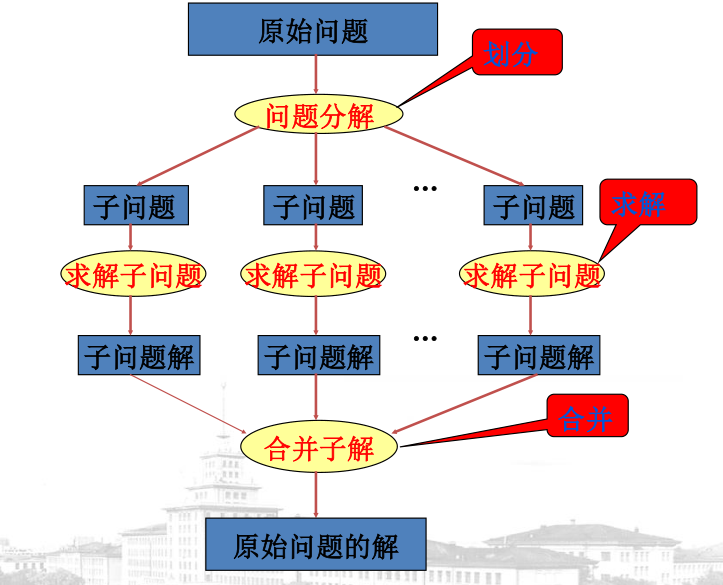
分治法的意思就是,分而治之,也就是把一个问题,拆分成几个小问题,最后再汇总解决的方法
通过大整数相乘问题来了解分治法
假如现在我们要求两个大整数相乘的乘积,如1234 * 1234(这里为了了分析简便,所以不举形如1234567891234567这样的大整数,不必要在此纠结),那么按照我们小学学的乘法,就是用乘数的每一项去和1234相乘,这样很明显,算法的时间复杂度是O(n^2),效率很低下,那么有没有一种更好的方式?我们可以使用分治法来解决。
算法分析
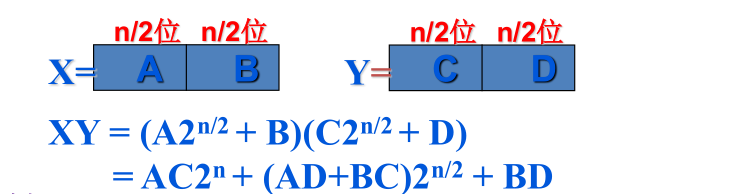
- 首先将X和Y分成A,B,C,D
- 此时将X和Y的乘积转化为图中的式子,把问题转化为求解式子的值
看起来好像有点变化,分析一下:对这个式子,我们一共要进行4次 n / 2的乘法(AC2次, AD, BC)和 3次加法,因而该算法的时间复杂度为:
T(n) = 4 * T(n / 2) + θ(n)
通过master定理可以求得 T(n) = θ(n ^ 2),跟小学算法的时间复杂度没有区别。
但是我们再来看看,我们是否可以用加法来换取乘法?因为多一个加法操作,也是常数项,对时间复杂度没有影响,如果减少一个乘法则不同。
XY=AC2^n+[(A-B)(D-C)+AC+BD]2^n/2+BD
现在的时间复杂度为:
T(n) = 3 * T(n / 2) + θ(n),通过master定理求得,T(n) = O(n^log2(3) ) = O(n^1.59 )。
Master定理:
Master定理实例:
时间复杂度O的意义
实例分析
对X = 1234 和 Y = 5678来分析:
divideConquer(1234, 5678, 4)
————————————————————————
X=1234 | A=12 | B=34 | A-B=-22
Y=5678 | C=56 | D=78 | D-C=22
三次递归:
AC = divideConquer(12, 56, 2)
BD = divideConquer(34, 78, 2)
(A-B)(D-C) = divideConquer(-22, 22, 2)
AC递归
————————————————————————
X=12 | A1=1 | B1=2 | A1-B1=-1
Y=56 | C1=5 | D1=6 | D1-C1=1
A1*C1 = divideConquer(1, 5, 1) = 5
B1*D1 = divideConquer(2, 6, 1) = 12
(A1-B1) * (D1-C1) = divideConquer(-1, 1, 1) = -1;
所以AC递归求得的值为:5 * 10 ^ 2 + (-1 + 5 + 12)* 10 + 12 = 672
同理可得 BD = 2652 和 (A-B)(D-C) = -484
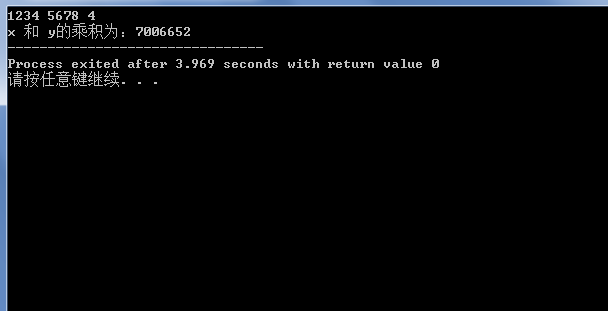
最终可得 X * Y = 7006652
代码实现
#include<cstdio>
#include<cmath>
using namespace std;
#define SIGN(A) ((A > 0) ? 1 : -1)
int divideConquer(int X, int Y, int n){
int sign = SIGN(X) * SIGN(Y);
int x = abs(X);
int y = abs(Y);
if(x == 0 || y == 0){
return 0;
}else if(n == 1){
return sign * x * y;
}else{
int A = (int) x / pow(10, (int)(n / 2));
int B = x - A * pow(10, n / 2);
int C = (int) y / pow(10, (int)(n / 2));
int D = y - C * pow(10, n / 2);
int AC = divideConquer(A, C, n / 2);
int BD = divideConquer(B, D, n / 2);
int ABDC = divideConquer((A - B), (D - C), n / 2) + AC + BD;
return sign * (AC * pow(10 , n) + ABDC * pow(10, (int)(n / 2)) + BD);
}
}
int main(){
int x, y, n;
scanf("%d%d%d", &x, &y, &n);
printf("x 和 y的乘积为:%d", divideConquer(x, y, n));
}结果:








 本文介绍了一种利用分治法提高大整数乘法效率的算法。通过对传统乘法方法的时间复杂度分析,引入分治法将问题分解为更小规模的子问题,并通过递归调用解决这些子问题,最终合并结果得到答案。此方法显著降低了时间复杂度。
本文介绍了一种利用分治法提高大整数乘法效率的算法。通过对传统乘法方法的时间复杂度分析,引入分治法将问题分解为更小规模的子问题,并通过递归调用解决这些子问题,最终合并结果得到答案。此方法显著降低了时间复杂度。



















 294
294

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








