机器学习算法 - 从线性回归到前馈神经网络

1.机器学习算法简介

 在本文中，关注的是预测任务，包括使用一组观察情况来预测结果。着重于以下方面:

    Regression（回归）:预测一个量(如距离、时间)，理解两个变量之间的关系。
    Classification（分类）:为输入分配一个离散的类别(如交通标志)。

 本文主要内容如下:

    线性回归
    逻辑回归
    梯度下降法优化
    前馈神经网络
    反向传播
    基于神经网络的图像分类

2.概述

在本文中，将创建ML模型，根据输入来预测输出。为了估计模型的拟合度，使用一个损失函数，并使用选定的度量标准对所创建的模型的性能进行量化。

模型:从输入中提取模式的一组计算。
损失函数/成本函数:将模型输出映射到单个实数的函数。
度量/标准:对算法性能进行量化的函数。

3.线性回归 

线性回归模型是ML算法的一种，假定输入变量和输出变量之间是线性关系。该模型由两个参数描述:斜率m和交点b，使y = mx +b。拟合或训练这样的模型需要调整m和b，使所选择的损失函数最小化。

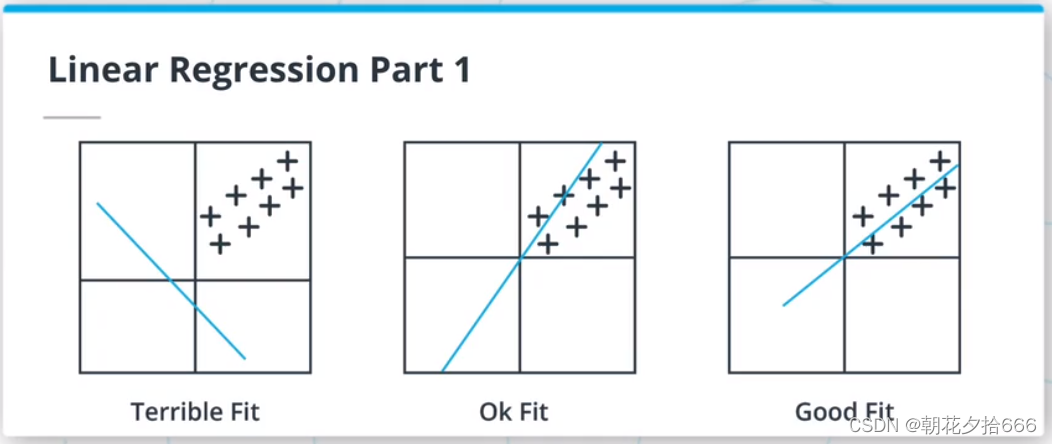
线性回归损失函数

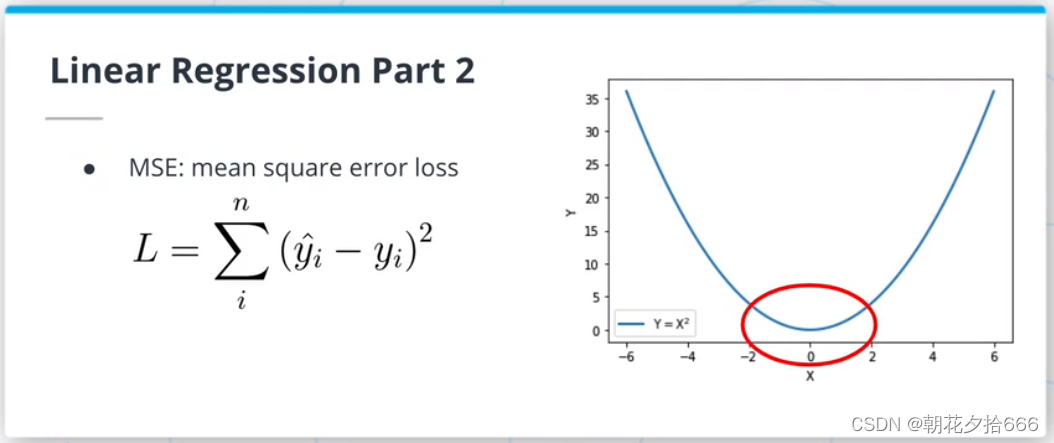
均方误差(MSE)损失或L2损失是线性回归算法中最常用的函数之一。它是通过对真实值和预测值的平方差求和来计算的。由于平方函数的性质，这种损失对异常值(分布数据点之外)非常敏感。

如果数据集包含许多异常值，L1损失(真实值和预测值之间的绝对差异)可能是一个更好的候选值。

4.逻辑回归Logistic Regression

对于分类问题，也可以用一个线性表达式来建模一个输入属于某一分类的概率P(Y|X)。这样的模型被称为逻辑回归，看起来像这样:P(Y|X) = mx+b。然而，考虑到要建模一个概率，需要一种方法来限制mx+b的值在[0,1]区间内。为此，将使用logistic函数(或sigmoid)。logistic函数将任意实数映射到[0,1]区间。

softmax函数是logistic函数到多个类的扩展，并以矢量而不是实数作为输入。softmax函数输出一个离散的概率分布:相似维度的向量作为输入，但其所有分量之和为1。在本文的后面，将描述sigmoid和softmax函数作为激活函数。

交叉熵损失和One-Hot编码

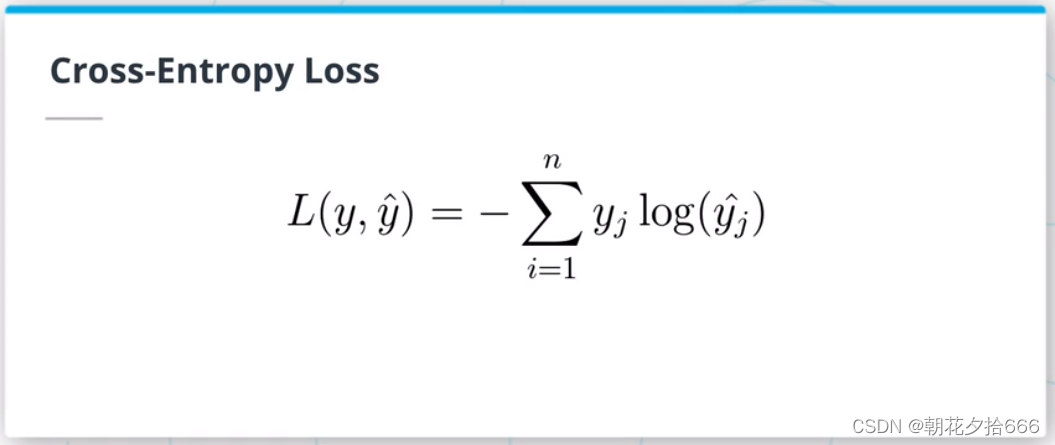
交叉熵(CE)损失是分类问题中最常见的损失。总损失等于所有观测值之和，即真实值one-hot编码向量和softmax概率向量的对数的点积。

对于多类分类问题，真实值标签需要编码为向量进行计算。一种常见的方法是one-hot编码方法，其中数据集的每个标签都被分配一个整数。这个整数被用作one-hot向量中仅有的非零元素的索引。

小结:对于分类问题，标签需要编码为C维的向量，其中C为数据集中类的数量。由于softmax函数，该模型输出了一个离散的概率分布向量，同样是C维的。为了计算输入和输出之间的交叉熵损失，我们计算了一个one hot向量和输出的对数的点积。

5.Tensorflow简介

Tensorflow张量是与numpy数组共享许多属性和特征的数据结构(例如.shape和广播规则)。它们确实有额外的属性，允许用户将张量从一个设备移动到另一个设备(例如cpu到gpu)。

6.练习1 -逻辑回归
目的
在这个练习中，实现四个不同的功能