代码随想录算法训练营第十六天| 104.二叉树的最大深度、 111.二叉树的最小深度、 222.完全二叉树的节点个数

104.二叉树的最大深度

参考文章：代码随想录 

参考视频：二叉树的高度和深度有啥区别？究竟用什么遍历顺序？很多录友搞不懂 | LeetCode：104.二叉树的最大深度_哔哩哔哩_bilibili 

解题思路：本质上是求左子树和右子树中的最大高度+1，采用后序遍历，将每个节点的左子树和右子树间的最大高度逐级从下往上传到根结点。

public int maxDepth(TreeNode root) {
        return getHeight(root);
    }

    public int getHeight(TreeNode node) {
        if (node == null) return 0;
        int left = getHeight(node.left);
        int right = getHeight(node.right);
        return 1 + Math.max(left, right);
    }

 111.二叉树的最小深度

参考文章：代码随想录 

参考视频：看起来好像做过，一写就错！ | LeetCode：111.二叉树的最小深度_哔哩哔哩_bilibili 

解题思路：本题的最小深度指的是从根节点到最近叶子节点的最短路径上的节点数量，

如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

public int minDepth(TreeNode root) {
        if (root == null) return 0;
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        if (root.left == null && root.right != null) {
            return right + 1;
        }
        if (root.left != null && root.right == null) {
            return left + 1;
        }
        return 1 + Math.min(left, right);
    }

222.完全二叉树的节点个数

参考文章：代码随想录 

参考视频：要理解普通二叉树和完全二叉树的区别！ | LeetCode：222.完全二叉树节点的数量_哔哩哔哩_bilibili

解题思路：如果是普通二叉树的话用普通的后序遍历即可算出总共的节点个数，时间复杂度为O(n)，而这题可利用完全二叉树的特性来减少时间复杂度。

大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。

我来举一个典型的例子如题：

 

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

完全二叉树（一）如图：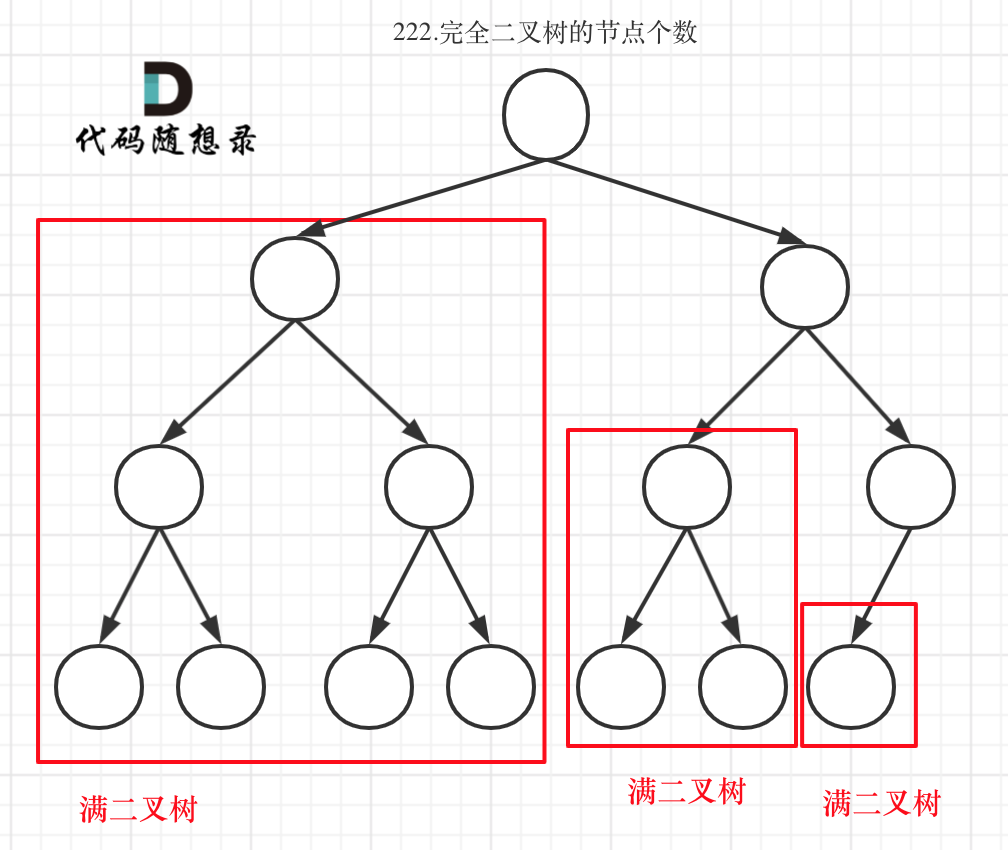 

完全二叉树（二）如图：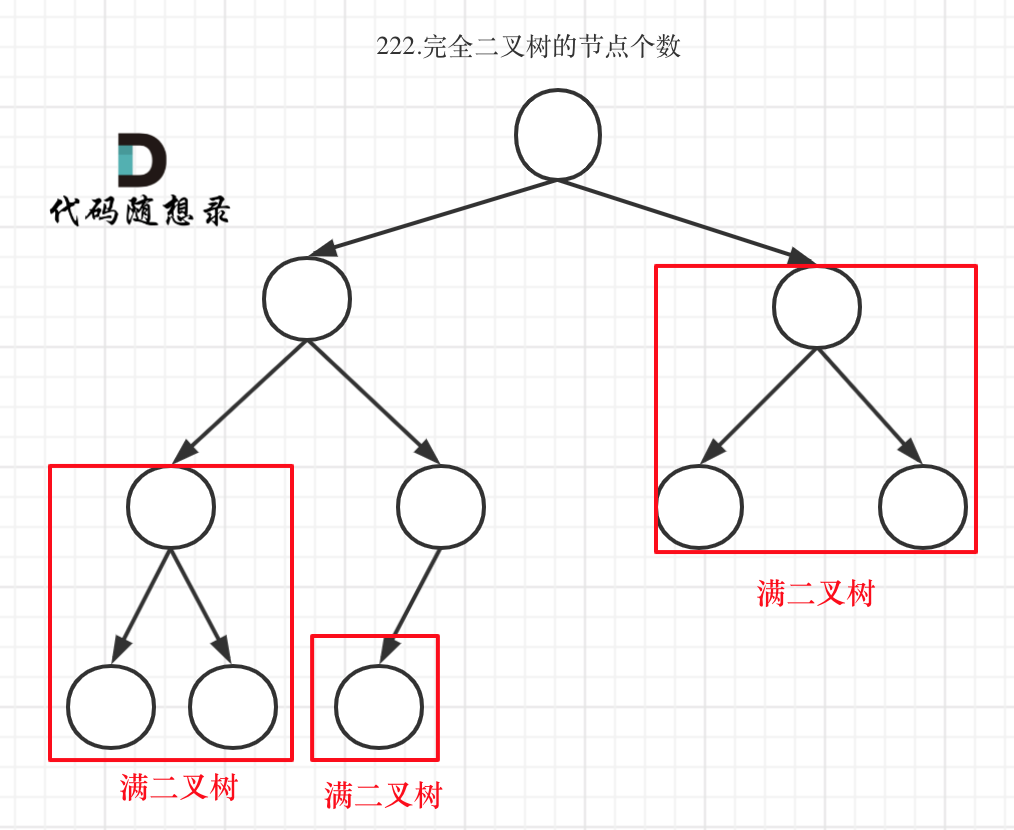 

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：

public int countNodes(TreeNode root) {
        if (root == null) return 0;
        TreeNode left = root.left;
        TreeNode right = root.right;
        int leftDepth = 0;
        int rightDepth = 0;
        while (left != null) {
            left = left.left;
            leftDepth++;
        }
        while (right != null) {
            right = right.right;
            rightDepth++;
        }
        
        if (leftDepth == rightDepth) return (int) Math.pow(2, leftDepth + 1) - 1; //return (2 << leftDepth) - 1;
        int leftNumber = countNodes(root.left);
        int rightNumber = countNodes(root.right);
        return leftNumber + rightNumber + 1;
    }