#SE test skill
1. printf 格式问题(空格,回车,数据类型)
2. 数据边界
3. 数据类型,例如TreeWeight要求mod(10000007),其中
(A * B * C ) % (10000007) 不等于
((A * B ) % (100000007) * C ) % (100000007)
#解题思路
1. 推导公式来解题
2. 从简单case入手观察规律
3. 从典型特征例子验证公式
#Bubbling sort
#define SWAP(A, B) \
do { \
int C; \
C = (A); \
(A) = (B); \
(B) = C; \
}while(0)
void desort(int * data, int num)
{
int i, j;
for (i = 0; i < num; i++)
for (j = i + 1; j < num; j++)
{
if (*(data + i) < *(data + j))
SWAP(*(data + i), *(data + j));
}
}
void sort(int * data, int num)
{
int i,j;
for (i = 0; i < num; i++)
for (j = i + 1; j < num; j++)
{
if (*(data + i) > *(data + j))
SWAP(*(data + i), *(data + j));
}
}
#动态规划算法
以下内容参考来源:http://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741374.html
基本概念
动态规划过程是:每次决策依赖于当前状态,又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。
基本思想是将待求解问题分解成若干子问题,先求解子问题,最后用这些子问题带到原问题,与分治算法的不同是,经分解得到的子问题往往是不是相互独立,若用分治则子问题太多
适用问题
求最优解问题,并且符合几个条件:
1. 最有子结构:最终问题的最优解包含子问题的最优解
2. 有重叠子问题:当问题维度逐渐扩大,子问题是重叠并可以复用的
解题思路
1. 按照时间和空间将问题分解成单个步骤,通常先通过最后一步来找出递归式公式,这样便很容易做出递归实现方式
2. 按照递归式公式,从问题的规模由小到大,来做出非递归算法实现
通常,递归式公式为:f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}
基本框架
复制代码
代码
1 for(j=1; j<=m; j=j+1) // 第一个阶段
2 xn[j] = 初始值;
3
4 for(i=n-1; i>=1; i=i-1)// 其他n-1个阶段
5 for(j=1; j>=f(i); j=j+1)//f(i)与i有关的表达式
6 xi[j]=j=max(或min){g(xi-1[j1:j2]), ......, g(xi-1[jk:jk+1])};
8
9 t = g(x1[j1:j2]); // 由子问题的最优解求解整个问题的最优解的方案
10
11 print(x1[j1]);
12
13 for(i=2; i<=n-1; i=i+1)
15 {
17 t = t-xi-1[ji];
18
19 for(j=1; j>=f(i); j=j+1)
21 if(t=xi[ji])
23 break;
25 }
典型实例
实例1 求最少路费
问题描述:不同公里数对应不同路费,例如1公里为5元,2公里为11元,3公里为19元,.....n公里为R(n)元,
求m公里的最少路费Y(m)。
解题分析:先从递归思想去推导最后一步,即最后一次公里数的选择有哪几种,
无非就是1公里,2公里,直到n公里,可见,最少路费一定从下面几种情况中选出,
Y(n-1) + R(1), Y(n-2) + R(2), ..... Y(m-n) + R(n), 包含n种情况,
总结为公式为:
Y(n) = min {Y(m-i) + R(i)} (i = 1,2, ... n)
若用递归算法很容易实现。
下面转化为非递归算法
Y(1) = R(1);
Y(2) = min {R(2), Y(1) + R(1)};
Y(3) = min {R(3), Y(2) + R(1), Y(1) + R(2)};
......
Y(n) = min {Y(m-n) + R(n), Y(m-n-1) + R(n-1), Y(m-1) + R(1)};
C codes :
#include <stdio.h>
int main(void)
{
int tc, T;
int R[10];
long long Y[10000+1];
int m,n;
int i,j,k;
int div,rem;
int min;
scanf("%d", &T);
for(tc = 0; tc < T; tc++)
{
for (i = 0; i < 10; i++) {
scanf("%d", &R[i]);
}
scanf("%d", &m);
Y[0] = 0;
for (i = 1; i <= m; i++) {
Y[i] = 99999999;
for (j = 0; j < 10 && (i >= j + 1); j++) {
Y[i] = ( Y[i-j-1] + R[j] < Y[i]) ? (Y[i-j-1] + R[j]) : Y[i];
}
}
printf("%d\n", Y[m]);
}
return 0;
}
实例2 矩阵乘法的最小乘积个数
M(mn)代表:第m个到第n个矩阵相乘的最小乘积次数
M(A)$M(B)代表:连续矩阵A和连续矩阵B的相乘次数,其中连续矩阵表示多个矩阵相乘后的矩阵,
例如M(A)为m*n矩阵,M(B)为n*p矩阵,那么M(A)$M(B)=m*n*p
递归解法:
考虑到最后一步一定是两个矩阵相乘,那么m个矩阵相乘最后一步可能存在m-1个情况,如下:
M(1)$M(2m), M(12)$M(3m), M(13)$M(4m), ,,, M(1(m-1))$M(m)
总结为公式为:
M(1m) = min{M(1)$M(2m), M(12)$M(3m), ... M(1(m-1))$M(m)}
非递归算法:
依次计算不同个数且相邻矩阵的最小乘法次数,例如总共六个矩阵的实例
M(mn)简写为Mmn
1. 两个相邻矩阵的情况:
M12 M23 M34 M45 M56
2. 三个相邻矩阵的情况:
M13 M24 M35 M46
3. 四个相邻矩阵的情况:
M14 M25 M36
4. 五个相邻矩阵的情况:
M15 M26
6. Final result留个相邻矩阵
M16
算法的关键是将上面的数据用适当的数据结构存储起来,
以便在扩大问题规模时,可以复用之前的结果
所以容易想到用矩阵,即二维数组来保存上面各个步骤的最优值
N is max number of Matrix
M(mn) means min multiplication time from Matrix m to Matrix n
V[N,N] is 2-dimensional array, V[i][j] means M(ij)
Line[N] is array stored number of line
Column[N] is array stored number of column
C fate codes:
for (i=1; i<=N; i++)
for (j=i; j<=N; j++)
for (k=i; k<=N; k++)
V[i][j] = min{V[1][k-1] + Line[k-1]*Column[k]*Column[k] + V[k][N]}
实例3 求最短路径问题【abolish】
题干:存在N个城市,存在M条城市间路线,并且每两个城市可达,求城市A到城市B的最短路线
Dmn:表示城市m到城市n存在一条直达路线,距离为Dmn
Pmn:城市m到城市n存在的可达路径最短值
N: total amount of cities
M: total amount of routines
已知Dmn和N,求Pij,即第j个城市到第i个城市的最短距离
递归思路解题
首先递归+分解,与i相邻的城市为a1,a2,... aM,
那么,Pij = min { D(i,a1) + P(a1,j), D(i, a2) + P(a2,j), ... D(i,aM) + P(aM,j) }
然后一步步递推,并且要满足递推公式中的城市a1,a2,...aM中不能包含当前最短路线中的城市,直到无法再拆解下去。
最终第j城市包含进来,计算出Pij。
注意:递归过程中要记录当前最短路线中的包含城市信息,
原因是,如果包含了最短路线中的城市,说明当前路线中存在环路,显然不会是最短路径。
非递归解题
借鉴矩阵连乘的思想,并且不太好找出以哪个城市为起点来逐渐扩大问题规模,
所以索性把问题转化为求解任意两个城市间最短距离的问题
用二维数组来存储任何两个城市间的最短距离,其中对角线上的数值相等,即aij=aji,而非只用二维数组的一半,
这样做的好处是遍历起来比较方便,下面的分析过程可以看出来。
首先将二维数组p[N][N]初始值为零,表示两个城市不可达。
然后依次输入两个城市的直达距离,并不断更新P[N][N]
例如加入D(a,b),需要更新与a和与b先关的所有路线的最短值,
这里是关键,如何找到规律去把与a和b相关的所有最短路线都更新呢?
分成两种情况:
第一种情况,城市a和城市b是最后一步,即城市a或者城市b为终点;
例如;import D(a,b), and c,d,e is adjacent to b, for example, P(c,a) = min{P(c,a), D(a,b)+P(c,b)}
另一种情况是城市a和城市b是中间某一步,这样便牵扯到与a可达的城市集合P和与b可达的城市集合Q,
任意从集合P挑一个城市x,从集合Q挑出一个城市y,那么新增D(a,b)会影响到Pxy的值
P(x,y) = min {P(x,y), P(x,a) + D(a,b) + P(y,b)}
C codes:
D[N][N] = {{0,5,2,10,0,8,0},{.......},....,{.......}}; //stored distance among cities
P[N][N] is mininus distance amnong cities
..... todo....
实例3' 求最短路径问题 迪杰斯特拉算法(Dijkstra算法)
reference:http://www.cnblogs.com/hxsyl/p/3270401.html
以下为引用部分
问题:从某顶点出发,沿图的边到达另一顶点所经过的路径中,各边上权值之和最小的一条路径——最短路径。解决最短路的问题有以下算法,Dijkstra算法,Bellman-Ford算法,Floyd算法和SPFA算法,另外还有著名的启发式搜索算法A*,不过A*准备单独出一篇,其中Floyd算法可以求解任意两点间的最短路径的长度。笔者认为任意一个最短路算法都是基于这样一个事实:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点到B。
以下部分来自:http://www.wutianqi.com/?p=1890
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
例如,对下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

实例4 完全二叉树最短叶子节点
找出从金字塔顶点到底端(即叶子节点)的最小加权路径
3
8 9
1 9 6
8 5 1 3
2 3 5 1 5
思路:动态优化算法
即,每个顶点到底端的最小路径是以下两条路径中较短的一个,
一个是到其左儿子节点路径 + 左儿子节点到底端最小路径的和,
另一个是到其右儿子节点路径 + 右儿子节点到底端最小路径的和
以上是递归思路解题
非递归算法:
问题的规模从小到大,这里从底端开始向顶来逐步扩大规模,
eg 最后一行的最小路径就认为是权值
2 3 5 1 5
倒数第二行的最小路径为
2+8 3+5 1+1 1+1 即 10 8 2 2,如下
10 8 2 2
2 3 5 1 5
倒数第三行的最小路径为
1+8 9+2 6+2 即 9, 11, 8,如下
9 11 8
10 8 2 2
2 3 5 1 5
第二行的最小路径为
8+9 9+8 即17 17,如下
17 17
9 11 8
10 8 2 2
2 3 5 1 5
可见最后的顶点到底端的最小距离为17+3 = 20
实例5 旅行者问题(TSP问题)
题目:存在N个城市,要求从第一个城市出发,依次经过其它N-1个城市并回到第一个城市,其中不能有重复的城市,求解最小路费。
已知:N个城市,M个路线(M(i,j)表示从第j个城市到第i个城市的费用
算法:动态规划+递归实现
reference:http://blog.csdn.net/joekwok/article/details/4749713
其中V‘是除去 i 以外的所有城市集合
Tips,可以从四个城市的简单例子,将上面的递归公式展开









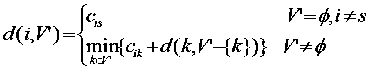














 5269
5269











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








