重温微积分

前言

数学是一个基本工具，微积分是这个基本工具的基础工具。本文记录笔者学习微积分中的主要心得，融合网上精华材料，以及自身的梳理总结。会不断完善之。

学习微积分也是一个先由薄到厚，再由厚到薄的过程。数学就是统一的, 应该让学生有一个统一的认识。当你把大学数学主要分支学完，就会产生这种体会。华罗庚当年搞一条龙教学，就是伟大的尝试。可惜现在许多大学还是割裂地教学，误人不浅，当然很多教师也是有心无力。

学习数学的数理观点

微积分的基本观点

多重积分的体积元素应有正负定向是大数学家Poincaré于19世纪末指出的，这一看似平凡的看法使得多元微积分产生了根本性的变革。

由微分的外乘积乘上函数组成的微分形式，称为外微分形式。
一次外微分形式，二次外微分形式，三次外微分形式的定义，分别对应于线积分、面积分、体积分。

Poincaré引理:若ω为一外微分形式，其微分形式的系数具有二阶连续偏导数，则ddω=0；
还可以有：
Poincaré引理之逆:若ω是一个p次外微分形式，且dω=0，则存在一个p-1次外微分形式α，使得ω=dα。

Stokes公式是微积分这门学科的一个顶峰，它使微积分从古典走向现代，是数学中少有的简洁、美丽而深刻的定理之一。

微积分知识体系

上述基础性课程体系：《数学分析Ⅰ》，《数学分析Ⅱ》以及《经典力学数学名著选讲（有关微积分的深化）》基本实现了基于有限维Euclid空间上微积分延拓至赋范线性空间上微分学、有限维Euclid空间中流形上微积分基础的进程，亦包括对有限维Euclid空间上微分学与积分学的深化——藉此，上述三门递进性课程就微积分研究的广度与深度可类比Zorich（卓里奇）著《数学分析》的程度。

微积分与外延

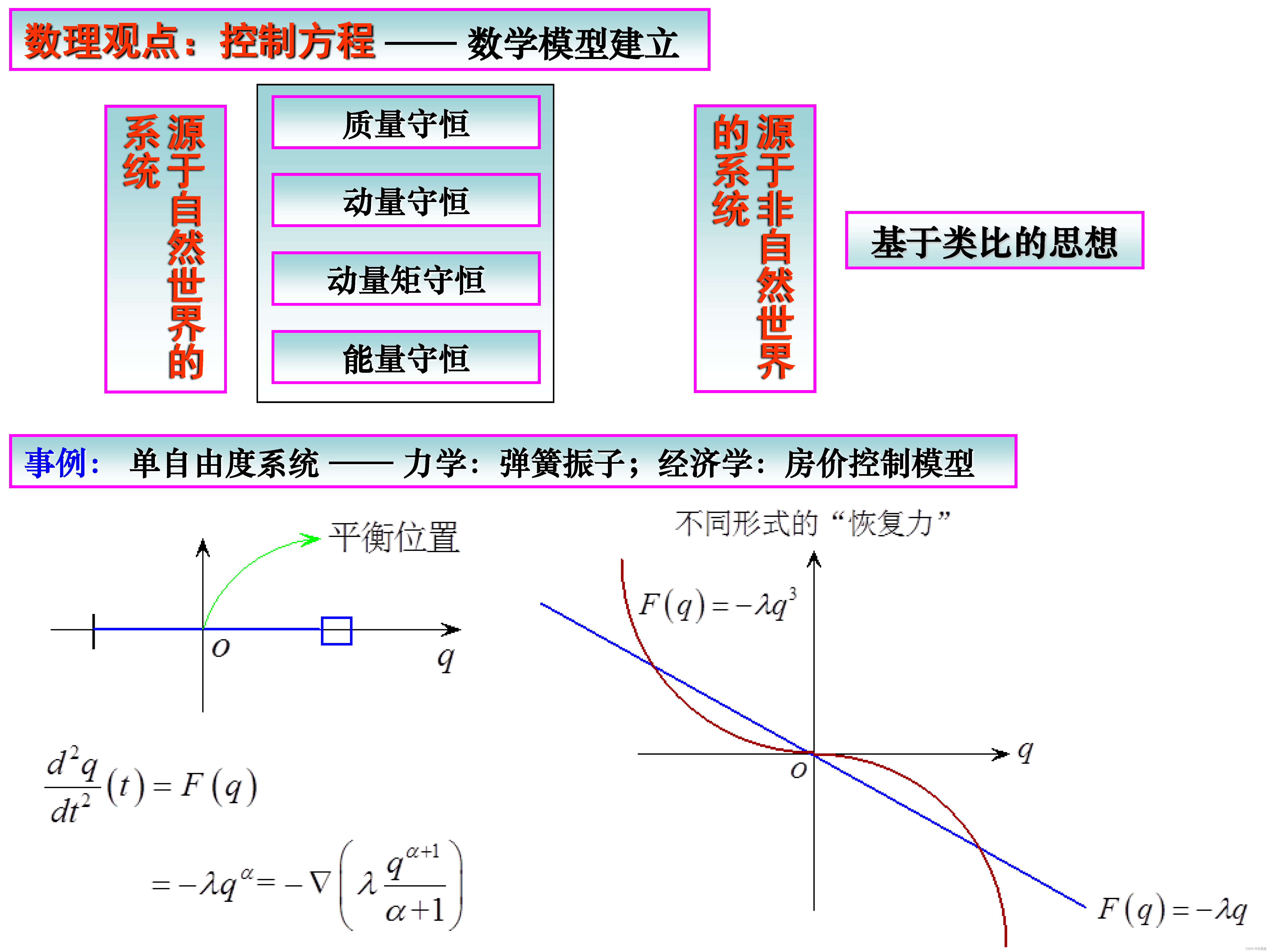
参考文献

• 复旦大学精品课程
• 《重温微积分_齐民友》高等教育出版社
• 《微积分五讲_龚昇》
• 《简明微积分(第四版龚昇)》