支持向量机系列---为什么要引入核函数

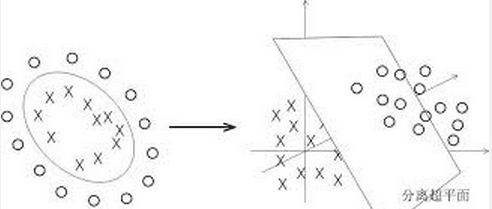
       前面的算法是针对线性可分的情况，当我们的样本线性不可分的时候怎么办呢？如果我们可以把线性不可分的问题转变成线性可分的问题该有多好！生活就是这么的美妙，我们可以将样本通过一个映射函数把它从原始空间投射到一个更高维的特征空间，使得样本在这特征空间线性可分，如下图所示。

这个时候，我们就可以对这个特征空间使用前面提到的最大化硬间间隔来进行分类。幸运的是，如果原始空间是有限维的，即属性数有限，那么一定存在一个高维特征空间使样本可分。

为了引出解决不可分的方法，我们先导入核函数。这个核函数是什么来头？我们先来看看核函数的定义 ：

设x,z∈X,X属于R（n）空间,非线性函数Φ实现输入间X到特征空间F的映射,其中F属于R（m）,n<<m。根据核函数技术有：

                                                                                                    K(x,z)=<Φ(x),Φ(z)>                
 其中：<, >为内积,Φ(x)为映射函数。

为了说明核函数的功能，很多资料上都举了下面这个例子，由于它的表述顺序，不少还是不知道核函数的作用，觉得它很抽象，其实我们应该倒过来理解。为什么我要这么说呢？我们来分析一下，到底核函数的作用是什么？