后端开发刷题 | 不同路径的数目

描述

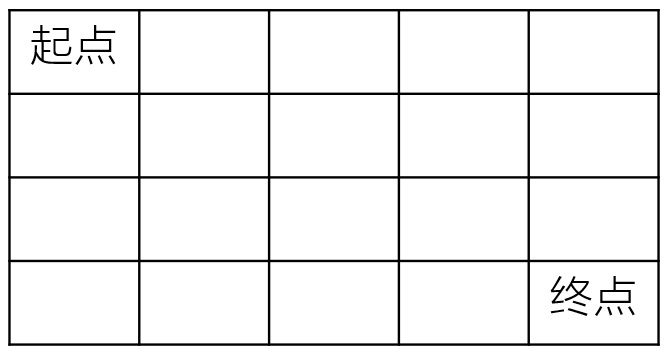
一个机器人在m×n大小的地图的左上角（起点）。

机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。

可以有多少种不同的路径从起点走到终点？

备注：m和n小于等于100,并保证计算结果在int范围内

数据范围：0<n,m≤100，保证计算结果在32位整型范围内

要求：空间复杂度 O(nm)，时间复杂度 O(nm)

进阶：空间复杂度 O(1)，时间复杂度 O(min(n,m))

示例1

输入：

2,1

返回值：

1

示例2

输入：

2,2

返回值：

2

思路分析：

该题可以使用递归或者动态规划来解决

动态规划

1. 初始化动态规划数组：dp 是一个二维数组，其中 dp[i][j] 表示到达网格中 (i, j) 这个位置的不同路径数量。数组的大小为 (m+1) x (n+1)，因为数组索引从 0 开始，而网格的坐标从 1 开始，所以数组的大小需要比网格的大小多一行一列，以便于处理边界情况。

2. 边界条件：在网格的第一行（i == 1）和第一列（j == 1）上，由于机器人只能向右或向下移动，所以到达这些位置的方式只有一种，即直接沿着边界到达。因此，dp[i][1] 和 dp[1][j]（对于所有 i 和 j）都被初始化为 1。

3. 状态转移方程：对于网格中的其他位置 (i, j)（即 i > 1 且 j > 1），到达该位置的不同路径数量等于从上方到达该位置的不同路径数量（dp[i-1][j]）加上从左方到达该位置的不同路径数量（dp[i][j-1]）。这是因为机器人可以从上方或左方到达 (i, j) 位置。

4. 返回结果：最终，dp[m][n] 存储了从左上角 (1, 1) 到达右下角 (m, n) 的不同路径数量，这就是函数的返回值。

代码：

import java.util.*;


public class Solution {
    /**
     * @param m int整型 
     * @param n int整型 
     * @return int整型
     */
    public int uniquePaths (int m, int n) {
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(i==1){
                    dp[i][j]=1;
                    continue;
                }

                if(j==1){
                    dp[i][j]=1;
                    continue;
                }

                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
}

递归

首先我们在左上角第一个格子的时候，有两种行走方式：如果向右走，相当于后面在一个(n−1)∗m(n−1)∗m的矩阵中查找从左上角到右下角的不同路径数；而如果向下走，相当于后面在一个n∗(m−1)n∗(m−1)的矩阵中查找从左上角到右下角不同的路径数。而(n−1)∗m(n−1)∗m的矩阵与n∗(m−1)n∗(m−1)的矩阵都是n∗mn∗m矩阵的子问题，因此可以使用递归。

具体做法：

• step 1：（终止条件） 当矩阵变长n减少到1的时候，很明显只能往下走，没有别的选择了，只有1条路径；同理m减少到1时也是如此。因此此时返回数量为1.
• step 2：（返回值） 对于每一级都将其两个子问题返回的结果相加返回给上一级。
• step 3：（本级任务） 每一级都有向下或者向右两种路径选择，分别进入相应分支的子问题。

代码：

import java.util.*;
public class Solution {
    public int uniquePaths (int m, int n) {
        //矩阵只要有一条边为1，路径数就只有一种了
        if(m == 1 || n == 1) 
            return 1;
        //两个分支
        return uniquePaths(m - 1, n) + uniquePaths(m, n - 1); 
    }
}