Bootle J , Cerulli A , Chaidos P , et al. Short Accountable Ring Signatures Based on DDH[C]// European Symposium on Research in Computer Security. Springer International Publishing, 2015.
Short Accountable Ring Signatures
Definition
- Setup ( 1 λ ) → p p \operatorname{Setup}\left(1^{\lambda}\right)\rightarrow pp Setup(1λ)→pp
- O K G e n ( p p ) → ( p k , d k ) \mathrm{OKGen}(p p)\rightarrow\left(pk,dk\right) OKGen(pp)→(pk,dk).Opener公私钥对,其中 p k = O K G e n ( p p , d k ) p k=\mathrm{OKGen}(p p, d k) pk=OKGen(pp,dk)
- U K G e n ( p p ) → ( v k , s k ) \mathrm{UKGen}(p p)\rightarrow\left(vk,sk\right) UKGen(pp)→(vk,sk).用户公私钥对,其中 v k = U K G e n ( p p , s k ) v k=\mathrm{UKGen}(p p, s k) vk=UKGen(pp,sk)
- Sign ( p k , m , R , s k ) → σ \operatorname{Sign}(p k, m, R, s k)\rightarrow\sigma Sign(pk,m,R,sk)→σ
- Vfy ( p k , m , R , σ ) → 0 / 1 \operatorname{Vfy}(p k, m, R, \sigma)\rightarrow0/1 Vfy(pk,m,R,σ)→0/1
- Open ( m , R , σ , d k ) → ( v k , ψ ) \operatorname{Open}(m, R, \sigma, d k)\rightarrow\left(vk,\psi\right) Open(m,R,σ,dk)→(vk,ψ). ψ \psi ψ是 v k vk vk的拥有者生成的签名的证明
- Judge ( p k , m , R , σ , v k , ψ ) → 0 / 1 \operatorname{Judge}(p k, m, R, \sigma, v k, \psi)\rightarrow0/1 Judge(pk,m,R,σ,vk,ψ)→0/1. 证明被接受,返回1;否则( σ \sigma σ无效或 v k vk vk)
四个性质:正确性、完全不可伪造性、匿名性和可追溯性。
Construction
通用构造:

注释:
f
f
f:one way function
Enc
\operatorname{Enc}
Enc:IND-CPA公钥加密
SoK
\operatorname{SoK}
SoK:signature of knowledge:
- SoKSetup ( g k ) → p p \operatorname{SoKSetup}(gk)\rightarrow{\bf pp} SoKSetup(gk)→pp
- SoKSign ( p p , s , w , m ) → σ S o K \operatorname{SoKSign}({\bf pp}, s, w, m)\rightarrow\sigma_{\rm{SoK}} SoKSign(pp,s,w,m)→σSoK. a statement s s s, a witness w w w
- SoKVerify ( p p , s , σ S o K ) → 0 / 1 \operatorname{SoKVerify}({\bf pp}, s, \sigma_{\rm{SoK}})\rightarrow0/1 SoKVerify(pp,s,σSoK)→0/1
NIZK \operatorname{NIZK} NIZK:
- CRSGen ( g k ) → c r s \operatorname{CRSGen}(gk)\rightarrow crs CRSGen(gk)→crs
- Prove ( c r s , s , w ) → π \operatorname{Prove}(crs,s,w)\rightarrow \pi Prove(crs,s,w)→π. a statement s s s, a witness w w w
- PVfy ( c r s , s , π ) → 0 / 1 \operatorname{PVfy}(crs,s,\pi)\rightarrow0/1 PVfy(crs,s,π)→0/1
思考:
- 为什么
Sign
\operatorname{Sign}
Sign算法中用来加密公钥的
Enc
\operatorname{Enc}
Enc和
SoKSign
\operatorname{SoKSign}
SoKSign使用同样的随机数
r
r
r?
A:因为 SoKSign \operatorname{SoKSign} SoKSign证明的就是 c = Enc p k ( v k ; r ) c=\operatorname{Enc}_{pk}(vk;r) c=Encpk(vk;r)的知识. -
Judge
\operatorname{Judge}
Judge算法中验证
π
\pi
π是statement
s
(
p
k
,
c
,
v
k
)
s(pk,c,vk)
s(pk,c,vk)的有效证明的的目的是?
A:Opener在签名系统中类似于组签名的中心化管理员,打开签名后给出(Opener的公钥(身份),被打开的签名密文,该签名的公钥(身份))的证明,将签名和签名者身份绑定。
Instantiation
基于DDH假设、
f
f
f指数群、
Enc
\operatorname{Enc}
Enc:ElGamal、
SoK
\operatorname{SoK}
SoK和
NIZK
\operatorname{NIZK}
NIZK:在证明如下关系的
Σ
\Sigma
Σ-协议上应用Fiat-Shamir变换
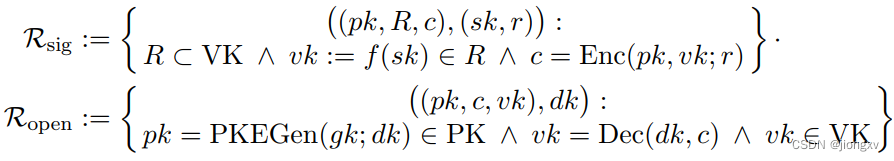
ElGamal算法:
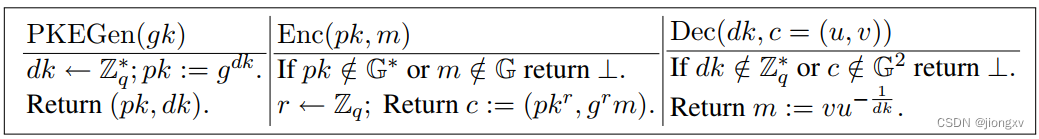
Pedersen Commitment:
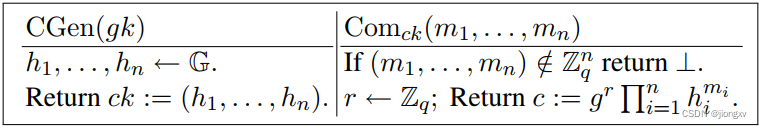
Σ \Sigma Σ-协议
关系
R
1
\mathcal{R}_1
R1:
B
B
B是一组bit序列的承诺,且每个
j
j
j对应的一组
b
j
,
?
b_{j,?}
bj,?只有一个是1。
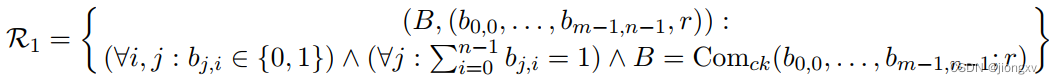
其实可分解成证明三个条件:①
b
j
,
i
(
1
−
b
j
,
i
)
=
0
b_{j,i}(1-b_{j,i})=0
bj,i(1−bj,i)=0 for all
i
,
j
i,j
i,j;②
∑
i
=
0
n
−
1
b
j
,
i
=
1
\sum_{i=0}^{n-1}b_{j,i}=1
∑i=0n−1bj,i=1 for all
j
j
j;③
B
=
Com
c
k
(
b
0
,
0
,
.
.
.
,
b
m
−
1
,
n
−
1
;
r
)
B= \operatorname{Com}_{ck}(b_{0,0},...,b_{m-1,n-1};r)
B=Comck(b0,0,...,bm−1,n−1;r).
证明 R 1 \mathcal{R}_1 R1的 Σ \Sigma Σ-协议:
Setup
:
g
k
,
c
r
s
:
=
(
c
k
,
e
k
)
\operatorname{Setup}: gk,crs:=(ck,ek)
Setup:gk,crs:=(ck,ek). 其中Pedersen承诺的
CGen
(
g
k
)
→
c
k
\operatorname{CGen}(gk)\rightarrow ck
CGen(gk)→ck;
ElGamal加密的
PKEGen
(
g
k
)
→
(
e
k
=
g
τ
,
τ
)
\operatorname{PKEGen}(gk)\rightarrow (ek=g^{\tau},\tau)
PKEGen(gk)→(ek=gτ,τ),
τ
←
Z
q
∗
\tau\leftarrow\mathbb{Z}_q^*
τ←Zq∗

分析:
- 设置
f
j
,
0
f_{j,0}
fj,0以满足条件②
f j , 0 ′ : = x − ∑ i = 1 n − 1 f j , i = x − ∑ i = 0 n − 1 f j , i + f j , 0 = x − ∑ i = 0 n − 1 ( b j , i x + a j , i ) + b j , 0 x + a j , 0 = x − ∑ i = 0 n − 1 b j , i x − ∑ i = 1 n − 1 a j , i + b j , 0 x = x − ∑ i = 0 n − 1 b j , i x + a j , 0 + b j , 0 x ( i f ∑ i = 0 n − 1 b j , i = 1 ) = a j , 0 + b j , 0 x \begin{aligned} f_{j,0}':&=x-\sum_{i=1}^{n-1}f_{j,i}\\ &=x-\sum_{i=0}^{n-1}f_{j,i}+f_{j,0}\\ &=x-\sum_{i=0}^{n-1}(b_{j,i}x+a_{j,i})+b_{j,0}x+a_{j,0}\\ &=x-\sum_{i=0}^{n-1}b_{j,i}x-\sum_{i=1}^{n-1}a_{j,i}+b_{j,0}x\\ &=x-\sum_{i=0}^{n-1}b_{j,i}x+a_{j,0}+b_{j,0}x\\ (if~\sum_{i=0}^{n-1}b_{j,i}=1)&=a_{j,0}+b_{j,0}x\\ \end{aligned} fj,0′:(if i=0∑n−1bj,i=1)=x−i=1∑n−1fj,i=x−i=0∑n−1fj,i+fj,0=x−i=0∑n−1(bj,ix+aj,i)+bj,0x+aj,0=x−i=0∑n−1bj,ix−i=1∑n−1aj,i+bj,0x=x−i=0∑n−1bj,ix+aj,0+bj,0x=aj,0+bj,0x - 第一个等式验证条件③
R H S = Com c k ( f 0 , 0 , . . . , f m − 1 , n − 1 ; z A ) = Com c k ( b 0 , 0 x + a 0 , 0 , . . . , b m − 1 , n − 1 x + a m − 1 , n − 1 ; r x + r A ) = Com c k ( b 0 , 0 x , . . . , b m − 1 , n − 1 x ; r x ) ⋅ Com c k ( a 0 , 0 , . . . , a m − 1 , n − 1 ; r A ) = Com c k ( b 0 , 0 , . . . , b m − 1 , n − 1 ; r ) x A ( i f B = Com c k ( b 0 , 0 , . . . , b m − 1 , n − 1 ; r ) ) = B x A = L H S \begin{aligned} RHS &= \operatorname{Com}_{ck}(f_{0,0},...,f_{m-1,n-1};z_A)\\ &= \operatorname{Com}_{ck}(b_{0,0}x+a_{0,0},...,b_{m-1,n-1}x+a_{m-1,n-1};rx+r_A)\\ &=\operatorname{Com}_{ck}(b_{0,0}x,...,b_{m-1,n-1}x;rx)\cdot\operatorname{Com}_{ck}(a_{0,0},...,a_{m-1,n-1};r_A)\\ &=\operatorname{Com}_{ck}(b_{0,0},...,b_{m-1,n-1};r)^xA\\ &(if~~B= \operatorname{Com}_{ck}(b_{0,0},...,b_{m-1,n-1};r))\\ &=B^xA=LHS \end{aligned} RHS=Comck(f0,0,...,fm−1,n−1;zA)=Comck(b0,0x+a0,0,...,bm−1,n−1x+am−1,n−1;rx+rA)=Comck(b0,0x,...,bm−1,n−1x;rx)⋅Comck(a0,0,...,am−1,n−1;rA)=Comck(b0,0,...,bm−1,n−1;r)xA(if B=Comck(b0,0,...,bm−1,n−1;r))=BxA=LHS - 第二个等式验证条件①
R H S = Com c k ( { f j , i ( x − f j , i ) } j , i = 0 m − 1 , n − 1 ; z C ) = Com c k ( { ( b j , i x + a j , i ) ( x − b j , i x − a j , i ) } j , i = 0 m − 1 , n − 1 ; r C x + r D ) = Com c k ( { b j , i ( 1 − b j , i ) x 2 + a j , i ( 1 − 2 b j , i ) x − a j , i 2 } j , i = 0 m − 1 , n − 1 ; r C x + r D ) = Com c k ( { b j , i ( 1 − b j , i ) } j , i = 0 m − 1 , n − 1 ; 0 ) x 2 ⋅ Com c k ( { a j , i ( 1 − 2 b j , i ) } j , i = 0 m − 1 , n − 1 ; r C ) x ⋅ Com c k ( { − a j , i 2 } j , i = 0 m − 1 , n − 1 ; r D ) = Com c k ( { b j , i ( 1 − b j , i ) } j , i = 0 m − 1 , n − 1 ; 0 ) x 2 C x D ( i f { b j , i ( 1 − b j , i ) } j , i = 0 m − 1 , n − 1 = 0 ) = C x D = L H S \begin{aligned} RHS&=\operatorname{Com}_{ck}(\{f_{j,i}(x-f_{j,i})\}_{j,i=0}^{m-1,n-1};z_C)\\ &=\operatorname{Com}_{ck}(\{(b_{j,i}x+a_{j,i})(x-b_{j,i}x-a_{j,i})\}_{j,i=0}^{m-1,n-1};r_Cx+r_D)\\ &=\operatorname{Com}_{ck}(\{b_{j,i}(1-b_{j,i})x^2+a_{j,i}(1-2b_{j,i})x-a_{j,i}^2\}_{j,i=0}^{m-1,n-1};r_Cx+r_D)\\ &=\operatorname{Com}_{ck}(\{b_{j,i}(1-b_{j,i})\}_{j,i=0}^{m-1,n-1};0)^{x^2}\cdot\operatorname{Com}_{ck}(\{a_{j,i}(1-2b_{j,i})\}_{j,i=0}^{m-1,n-1};r_C)^x\cdot\operatorname{Com}_{ck}(\{-a_{j,i}^2\}_{j,i=0}^{m-1,n-1};r_D)\\ &=\operatorname{Com}_{ck}(\{b_{j,i}(1-b_{j,i})\}_{j,i=0}^{m-1,n-1};0)^{x^2}C^xD\\ &(if ~\{b_{j,i}(1-b_{j,i})\}_{j,i=0}^{m-1,n-1}=0)\\ &=C^xD=LHS \end{aligned} RHS=Comck({fj,i(x−fj,i)}j,i=0m−1,n−1;zC)=Comck({(bj,ix+aj,i)(x−bj,ix−aj,i)}j,i=0m−1,n−1;rCx+rD)=Comck({bj,i(1−bj,i)x2+aj,i(1−2bj,i)x−aj,i2}j,i=0m−1,n−1;rCx+rD)=Comck({bj,i(1−bj,i)}j,i=0m−1,n−1;0)x2⋅Comck({aj,i(1−2bj,i)}j,i=0m−1,n−1;rC)x⋅Comck({−aj,i2}j,i=0m−1,n−1;rD)=Comck({bj,i(1−bj,i)}j,i=0m−1,n−1;0)x2CxD(if {bj,i(1−bj,i)}j,i=0m−1,n−1=0)=CxD=LHS
关系
R
2
\mathcal{R}_2
R2:N个ElGamal密文中包含一个对1的加密.
![]()
思路:
设
N
=
n
m
N=n^m
N=nm(可用最后一个密文的副本填充);协议要证明的关系等价转换为证明
∏
i
=
0
N
−
1
c
i
δ
ℓ
,
i
\prod_{i=0}^{N-1} c_{i}^{\delta_{\ell,i }}
∏i=0N−1ciδℓ,i是一个对1的加密(
δ
j
,
i
\delta_{j,i }
δj,i是Kronecker’s delta,即,
δ
ℓ
,
ℓ
=
1
\delta_{\ell ,\ell}=1
δℓ,ℓ=1 and
δ
ℓ
,
i
=
0
\delta_{\ell,i}=0
δℓ,i=0 for
i
≠
ℓ
i \neq \ell
i=ℓ)
- Prover首先提交m个n bits序列 ( δ ℓ j , 0 , . . . , δ ℓ j , n − 1 ) (\delta_{\ell_j,0},...,\delta_{\ell_j,n-1}) (δℓj,0,...,δℓj,n−1)的承诺.执行证明关系 R 1 \mathcal{R}_1 R1的协议证明这个承诺(这步证明的作用是证明Kronecker’s delta序列的良好形式)。
- 收到挑战
x
x
x,Prover公开
R
1
\mathcal{R}_1
R1中的元素
f
j
,
i
=
δ
ℓ
j
,
i
x
+
a
j
,
i
f_{j,i}=\delta_{\ell_j,i}x+a_{j,i}
fj,i=δℓj,ix+aj,i;观察每个
i
∈
{
0
,
.
.
.
,
N
−
1
}
i\in\{0,...,N-1\}
i∈{0,...,N−1},连乘积
∏
j
=
0
m
−
1
f
j
,
i
j
\prod_{j=0}^{m-1} f_{j,i_j}
∏j=0m−1fj,ij是多项式
p
i
(
x
)
=
∏
j
=
0
m
−
1
δ
ℓ
j
,
i
x
+
a
j
,
i
p_i(x)= \prod_{j=0}^{m-1}\delta_{\ell_j,i}x+a_{j,i}
pi(x)=∏j=0m−1δℓj,ix+aj,i在
x
x
x处的值。对于
0
⩽
i
⩽
N
−
1
0\leqslant i \leqslant N-1
0⩽i⩽N−1:
p i ( x ) = ∏ j = 0 m − 1 δ ℓ j , i j x + ∑ k = 0 m − 1 p i , k x k = δ ℓ , i x m + ∑ k = 0 m − 1 p i , k x k \begin{aligned} p_i(x)= \prod_{j=0}^{m-1}\delta_{\ell_j,i_j}x+\sum_{k=0}^{m-1}p_{i, k} x^{k}=\delta_{\ell,i}x^m+\sum_{k=0}^{m-1}p_{i, k} x^{k} \end{aligned} pi(x)=j=0∏m−1δℓj,ijx+k=0∑m−1pi,kxk=δℓ,ixm+k=0∑m−1pi,kxk
( p i , k p_{i, k} pi,k是多项式的k次系数,它的值取决于 ℓ \ell ℓ和 a j , i a_{j,i} aj,i,它可以被Prover独立于x的取值计算出来;而 p ℓ ( x ) p_\ell(x) pℓ(x)是在 p 0 ( x ) , . . . , p N − 1 ( x ) p_0(x),...,p_{N-1}(x) p0(x),...,pN−1(x)中唯一的m维多项式) - 用这些系数和一些随机值,计算密文
G
k
G_k
Gk,它被用来抵消
p
i
(
x
)
p_i(x)
pi(x)中的低次项。
证明 R 2 \mathcal{R}_2 R2的 Σ \Sigma Σ-协议:

分析:
(黄色标记)对关系 R 1 \mathcal{R}_1 R1的证明
(绿色标记)对关系 R 2 \mathcal{R}_2 R2的证明(注意ElGamal具有同态性质)
L H S = ∏ i = 0 N − 1 c i ∏ j = 1 m f j , i j ⋅ ∏ k = 0 m − 1 G k − x k = ∏ i = 0 N − 1 c i δ ℓ , i x m + ∑ k = 0 m − 1 p i , k x k ⋅ ∏ k = 0 m − 1 ( ∏ i = 0 N − 1 c i p i , k ⋅ Enc e k ( 1 ; ρ k ) ) − x k = ∏ i = 0 N − 1 c i δ ℓ , i x m ⋅ ∏ i = 0 N − 1 ( ∏ k = 0 m − 1 c i p i , k x k ) ⋅ ∏ k = 0 m − 1 ( ∏ i = 0 N − 1 c i − p i , k x k ) ⋅ ∏ k = 0 m − 1 Enc e k ( 1 ; ρ k ) − x k = c ℓ x m ⋅ ∏ k = 0 m − 1 Enc e k ( 1 ; ρ k ) − x k = c ℓ x m ⋅ Enc e k ( 1 m ; − ∑ k = 0 m − 1 ρ k x k ) ( i f c ℓ = Enc e k ( 1 ; r ) ) = Enc e k ( 1 ; r x m ) ⋅ Enc e k ( 1 ; − ∑ k = 0 m − 1 ρ k x k ) = Enc e k ( 1 ; z ) = R H S \begin{aligned} LHS&=\prod_{i=0}^{N-1} c_{i}^{\prod_{j=1}^{m} f_{j, i_{j}}} \cdot \prod_{k=0}^{m-1} G_{k}^{-x^{k}}\\ &=\prod_{i=0}^{N-1} c_{i}^{\delta_{\ell,i}x^m+\sum_{k=0}^{m-1}p_{i, k} x^{k}} \cdot \prod_{k=0}^{m-1} (\prod_{i=0}^{N-1} c_{i}^{p_{i,k}}\cdot \operatorname{Enc}_{ek}(1;\rho_k))^{-x^{k}}\\ &=\prod_{i=0}^{N-1} c_{i}^{\delta_{\ell,i}x^m}\cdot \prod_{i=0}^{N-1}(\prod_{k=0}^{m-1}c_i^{p_{i, k} x^{k}})\cdot \prod_{k=0}^{m-1} (\prod_{i=0}^{N-1} c_{i}^{-p_{i,k}x^{k}})\cdot \prod_{k=0}^{m-1}\operatorname{Enc}_{ek}(1;\rho_k)^{-x^{k}}\\ &=c_{\ell}^{x^m}\cdot \prod_{k=0}^{m-1}\operatorname{Enc}_{ek}(1;\rho_k)^{-x^{k}}\\ &=c_{\ell}^{x^m}\cdot \operatorname{Enc}_{ek}(1^m;-\sum_{k=0}^{m-1}\rho_kx^k)\\ (if~c_{\ell}=\operatorname{Enc}_{ek}(1;r))&=\operatorname{Enc}_{ek}(1;rx^m)\cdot \operatorname{Enc}_{ek}(1;-\sum_{k=0}^{m-1}\rho_kx^k)\\ &=\operatorname{Enc}_{ek}(1;z)=RHS \end{aligned} LHS(if cℓ=Encek(1;r))=i=0∏N−1ci∏j=1mfj,ij⋅k=0∏m−1Gk−xk=i=0∏N−1ciδℓ,ixm+∑k=0m−1pi,kxk⋅k=0∏m−1(i=0∏N−1cipi,k⋅Encek(1;ρk))−xk=i=0∏N−1ciδℓ,ixm⋅i=0∏N−1(k=0∏m−1cipi,kxk)⋅k=0∏m−1(i=0∏N−1ci−pi,kxk)⋅k=0∏m−1Encek(1;ρk)−xk=cℓxm⋅k=0∏m−1Encek(1;ρk)−xk=cℓxm⋅Encek(1m;−k=0∑m−1ρkxk)=Encek(1;rxm)⋅Encek(1;−k=0∑m−1ρkxk)=Encek(1;z)=RHS
关系
R
s
i
g
\mathcal{R}_{\rm{sig}}
Rsig的
Σ
\Sigma
Σ-协议:
![]()
 分析:
分析:
P
s
i
g
\mathcal{P}_{\rm{sig}}
Psig中设置
d
d
d的作用是,消减掉
v
k
vk
vk的加密变为1的加密,便于使用
R
2
\mathcal{R}_2
R2的证明one-out-of-n是1的加密(环签名)。
- 第一个等式验证:
v
k
=
g
s
k
vk=g^{sk}
vk=gsk,
c
=
Enc
p
k
(
v
k
;
r
)
c=\operatorname{Enc}_{pk}(vk;r)
c=Encpk(vk;r)
R H S = Enc p k ( g z s ; z a ) = Enc p k ( g s k ⋅ x + s ; r x + r a ) = Enc p k ( g s k ; r ) x ⋅ Enc p k ( g s ; r a ) ( i f g s k = v k ) = Enc p k ( v k ; r ) x A ( i f Enc p k ( v k ; r ) = c ) = c x A = L H S \begin{aligned} RHS&=\operatorname{Enc}_{pk}(g^{z_s};z_a)\\ &=\operatorname{Enc}_{pk}(g^{sk\cdot x+s};rx+r_a)\\ &=\operatorname{Enc}_{pk}(g^{sk};r)^{x}\cdot\operatorname{Enc}_{pk}(g^{s};r_a)\\ (if~g^{sk}=vk)&=\operatorname{Enc}_{pk}(vk;r)^xA\\ (if~\operatorname{Enc}_{pk}(vk;r)=c)&=c^xA=LHS \end{aligned} RHS(if gsk=vk)(if Encpk(vk;r)=c)=Encpk(gzs;za)=Encpk(gsk⋅x+s;rx+ra)=Encpk(gsk;r)x⋅Encpk(gs;ra)=Encpk(vk;r)xA=cxA=LHS - 第二个等式验证:
R H S = Enc e k ( g z s ; z b ) = Enc e k ( g s k ⋅ x + s ; t x + r b ) = Enc e k ( g s k ; t ) x ⋅ Enc e k ( g s ; r b ) = d x B \begin{aligned} RHS&=\operatorname{Enc}_{ek}(g^{z_s};z_b)\\ &=\operatorname{Enc}_{ek}(g^{sk\cdot x+s};tx+r_b)\\ &=\operatorname{Enc}_{ek}(g^{sk};t)^{x}\cdot\operatorname{Enc}_{ek}(g^{s};r_b)\\ &=d^xB \end{aligned} RHS=Encek(gzs;zb)=Encek(gsk⋅x+s;tx+rb)=Encek(gsk;t)x⋅Encek(gs;rb)=dxB
思考:作用是什么?
A:注意只有 d d d是正确的才能使 R 2 \mathcal{R}_2 R2的证明验证有效,则 d d d的两个参数正确性需要得到保证: t t t可由挑战 x x x生成的 z b z_b zb验证, g s k g^{sk} gsk可由公开的 v k vk vk验证( g s k g^sk gsk和 v k vk vk的等价关系第一个等式已保证) - 第三个等式验证:one-out-of-n签名关系,即密文 c 0 , . . . , c N − 1 c_0,...,c_{N-1} c0,...,cN−1中有一个是1的加密。
关系
R
o
p
e
n
\mathcal{R}_{\rm{open}}
Ropen的
Σ
\Sigma
Σ-协议:
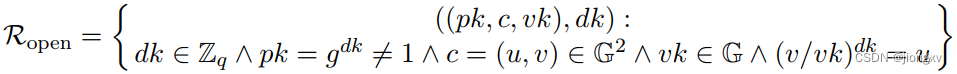
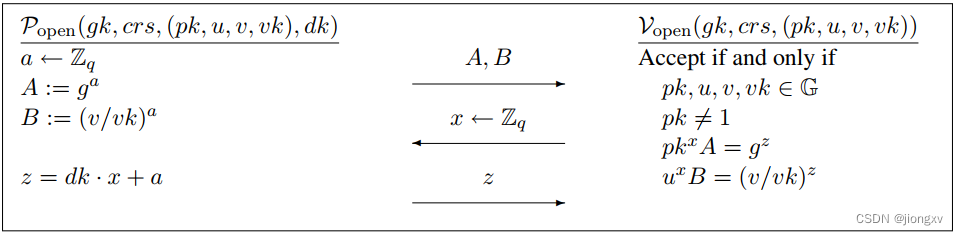
分析:
R
H
S
=
g
z
=
g
d
k
⋅
x
+
a
(
i
f
g
d
k
=
p
k
)
=
p
k
x
⋅
g
a
=
p
k
x
A
=
L
R
S
\begin{aligned} RHS&=g^z=g^{dk\cdot x+a}\\ (if~g^{dk}=pk)&={pk}^x \cdot g^a={pk}^xA=LRS \end{aligned}
RHS(if gdk=pk)=gz=gdk⋅x+a=pkx⋅ga=pkxA=LRS
R
H
S
=
(
v
/
v
k
)
z
=
(
v
/
v
k
)
d
k
⋅
x
+
a
(
i
f
(
v
/
v
k
)
d
k
=
u
)
=
u
x
⋅
(
v
/
v
k
)
a
=
u
x
B
=
L
R
S
\begin{aligned} RHS&=(v/vk)^z=(v/vk)^{dk\cdot x+a}\\ (if~(v/vk)^{dk}=u)&=u^x \cdot (v/vk)^a=u^xB=LRS \end{aligned}
RHS(if (v/vk)dk=u)=(v/vk)z=(v/vk)dk⋅x+a=ux⋅(v/vk)a=uxB=LRS
方案的效率
为什么叫short签名呢?
传输效率
首先,方案的效率由
P
s
i
g
\mathcal{P}_{\rm{sig}}
Psig的知识签名决定。对于一个规模为
N
=
n
m
N=n^m
N=nm个用户组成的环,证明者在签名中嵌套调用了
R
2
\mathcal{R}_2
R2和
R
1
\mathcal{R}_1
R1的证明,传输参数包括:
m
+
4
m+4
m+4个ElGamal密文,4个Pedersen 承诺,
m
(
n
−
1
)
+
6
m(n-1)+6
m(n−1)+6个
Z
q
\mathbb{Z}_q
Zq参数:
- P 1 : { A , C , D } ∈ Comitment × 3 , { f 0 , 1 , . . . , f m − 1 , n − 1 } ∈ Ciphertext × m ( n − 1 ) , { z A , z C } ∈ Z q × 2 \mathcal{P}_1:\{A,C,D\}\in \operatorname{Comitment}\times3,\{f_{0,1},...,f_{m-1,n-1}\}\in \operatorname{Ciphertext}\times m(n-1),\{z_A,z_C\}\in\mathbb{Z}_q\times2 P1:{A,C,D}∈Comitment×3,{f0,1,...,fm−1,n−1}∈Ciphertext×m(n−1),{zA,zC}∈Zq×2.
- P 2 / P 1 : B ∈ Comitment × 1 , { G k } k = 0 m − 1 ∈ Ciphertext × m , z ∈ Z q × 1 \mathcal{P}_2/\mathcal{P}_1:B\in \operatorname{Comitment}\times 1,\{G_k\}_{k=0}^{m-1}\in\operatorname{Ciphertext}\times m,z\in\mathbb{Z}_q\times1 P2/P1:B∈Comitment×1,{Gk}k=0m−1∈Ciphertext×m,z∈Zq×1.
- P 3 / P 2 : { d , A , B , c } ∈ Ciphertext × 3 , { z a , z b , z s } ∈ Z q × 3 \mathcal{P}_3/\mathcal{P}_2:\{d,A,B,c\}\in\operatorname{Ciphertext}\times 3,\{z_a,z_b,z_s\}\in\mathbb{Z}_q\times3 P3/P2:{d,A,B,c}∈Ciphertext×3,{za,zb,zs}∈Zq×3.(注意 c c c虽然不在协议的send部分,但它不属于公共参数,也是需要传输的)
每个ElGamal密文包含2个群元素,Pedersen 承诺包含1个群元素。所以整个Accountable ring signature方案共传输了
2
m
+
12
2m+12
2m+12个群元素和
m
(
n
−
1
)
+
6
m(n-1)+6
m(n−1)+6个域元素。
计算效率
生成签名共
m
N
+
3
m
n
+
2
m
+
12
mN+3mn+2m+12
mN+3mn+2m+12个组幂运算:
- 计算 A , C , D : 2 m n + 3 A,C,D:2mn+3 A,C,D:2mn+3(根据Pedersen 承诺的定义, A , C , D A,C,D A,C,D中各有 m + 1 m+1 m+1次幂计算,但 C C C中由于其系数 ( 1 − 2 b i , j ) = ± 1 (1-2b_{i,j})=\pm 1 (1−2bi,j)=±1的关系,其 m m m次幂运算只相当于在 A A A上多做了一次乘法)
- P s i g \mathcal{P}_{\rm{sig}} Psig协议构造 c i c_i ci,并作为输入在调用 P 2 \mathcal{P}_2 P2中计算乘幂,所有 c i c_i ci的第一个分量都相同的(因为随机数都是 t t t),所以 P 2 \mathcal{P}_2 P2中计算 { G k } k = 0 m − 1 \{G_k\}_{k=0}^{m-1} {Gk}k=0m−1共消耗 2 m 2m 2m次幂计算(前半部分关于 p i , k m p_{i,k}~m pi,k m次,后半部分关于 ρ k m \rho_{k}~m ρk m次);所有 G k G_k Gk的第二个分量需要 m N + m mN + m mN+m次幂计算.
- 计算 P 2 \mathcal{P}_2 P2中的 B × 1 B\times1 B×1次, P s i g \mathcal{P}_{\rm{sig}} Psig中的 { d , A , B } \{d,A,B\} {d,A,B}共 ( 3 × 2 ) (3\times2) (3×2)次,以及${d,A,B}$中被ElGamal加密的明文中有2次乘幂计算;总计:9次。
验证签名共 N + 2 m n + 2 m + 15 N + 2mn + 2m + 15 N+2mn+2m+15个组幂计算:
- V 2 \mathcal{V}_2 V2中最后一个验证式: ( N + 1 ) + 2 m + 2 = N + 2 m + 3 (N+1)+2m+2=N+2m+3 (N+1)+2m+2=N+2m+3.
- V 1 \mathcal{V}_1 V1中的2个等式各: 1 + ( m n + 1 ) 1+(mn+1) 1+(mn+1)次,共 2 m n + 4 2mn+4 2mn+4次.
- V s i g \mathcal{V}_{\rm{sig}} Vsig的前两个等式各: ( 2 + 2 ) (2+2) (2+2)次,共 8 8 8次.
n的取值
这个方案可以在DDH问题计算困难的任何
G
\mathbb{G}
G群上实例化。设安全参数
λ
\lambda
λ决定域元素的bit规模为
∣
q
∣
≈
λ
|q| \approx \lambda
∣q∣≈λ 位,设
N
=
p
o
l
y
(
λ
)
N = poly(\lambda)
N=poly(λ)。当群元素比域元素大得多,即大于因子
λ
\lambda
λ时,选择一个较大的n是方便的。例如,设
n
=
λ
+
1
n = \lambda+ 1
n=λ+1(在这种情况下
m
=
O
(
1
)
m = O(1)
m=O(1)),通信复杂度等于常数个数的群元素和
m
λ
+
6
mλ + 6
mλ+6个域元素。当群和域元素的大小大致相同时,就像椭圆曲线组的情况一样,我们的签名总大小为
m
(
n
+
1
)
+
18
m(n + 1) + 18
m(n+1)+18个元素。设置
n
=
4
n = 4
n=4,通信开销大约为
5
l
o
g
4
N
+
18
=
5
2
l
o
g
2
n
+
18
5 log_4 N + 18 = \frac{5}{2} log_2 n + 18
5log4N+18=25log2n+18.
m
(
n
+
1
)
+
18
=
5
m
+
18
(
n
m
=
N
)
=
5
l
o
g
n
N
+
18
=
5
l
o
g
4
N
+
18
\begin{aligned} m(n + 1) + 18&=5m+18\\ (n^m=N)&=5log_n N+18=5log_4N+18 \end{aligned}
m(n+1)+18(nm=N)=5m+18=5lognN+18=5log4N+18






















 303
303











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








