下面是用邻接表存储无向图,然后输出图中指定顶点间的指定长度的简单路径,简单路径就是路径中的顶点不重复,还有一个就是求出图中经过某顶点的回路,都是对图的遍历算法的应用,主要是深度优先的遍历,加上简单的回溯。
下面是代码:
//文件"graph.h"
#include <iostream>
#include <string>
#include <queue>
using namespace std;
bool visited[20];
int path[20];
struct ArcNode
{
int adjvex;
ArcNode *nextarc;
};
struct VexNode
{
string data;
ArcNode *firstarc;
};
class NDGraph
{
private:
VexNode vertices[20];
int vexnum;
int arcnum;
public:
NDGraph()
{
vexnum=0;
arcnum=0;
}
int GetVexNum()
{
return vexnum;
}
int Locate_Vex(string v)
{
for(int i=0;i<vexnum;i++)
if(vertices[i].data == v)
return i;
return -1;
}
void Create_NDGraph()
{
//构造无向图
string v1,v2;
int i,j,k;
cout<<"输入顶点数和边数:";
cin>>vexnum>>arcnum;
while(vexnum>20)
{
cout<<"请输入少于20个顶点(重新输入顶点数和边数):";
cin>>vexnum>>arcnum;
}
cout<<"输入顶点名称:";
for(i=0;i<vexnum;i++)
{
cin>>vertices[i].data;
vertices[i].firstarc=NULL;
}
for(k=0;k<arcnum;k++)
{
cout<<"输入每条边对应的两个顶点:";
cin>>v1>>v2;
i=Locate_Vex(v1);
j=Locate_Vex(v2);
while(i == -1 || j == -1)
{
cout<<"顶点中有不符合要求的,请重新输入:";
cin>>v1>>v2;
i=Locate_Vex(v1);
j=Locate_Vex(v2);
}
ArcNode *p=new ArcNode;
p->adjvex=j;
p->nextarc=vertices[i].firstarc;
vertices[i].firstarc=p;
//置对称边
ArcNode *q=new ArcNode;
q->adjvex=i;
q->nextarc=vertices[j].firstarc;
vertices[j].firstarc=q;
}
cout<<"无向图构造完成"<<endl;
}
void DFS_Traverse()
{
for(int i=0;i<vexnum;i++)
visited[i]=false;
for(i=0;i<vexnum;i++)
if(!visited[i])
DFS(i);
}
void DFS(int v)
{
visited[v]=true;
cout<<vertices[v].data<<" ";
ArcNode *p;
int w;
for(p=vertices[v].firstarc;p;p=p->nextarc)
{
w=p->adjvex;
if(!visited[w])
DFS(w);
}
}
void BFS_Traverse()
{
for(int i=0;i<vexnum;i++)
visited[i]=false;
for(i=0;i<vexnum;i++)
if(!visited[i])
BFS(i);
}
void BFS(int v)
{
visited[v]=true;
cout<<vertices[v].data<<" ";
queue<int> qu;
int w,k;
ArcNode *p=NULL;
qu.push(v);
while(!qu.empty())
{
w=qu.front();
qu.pop();
for(p=vertices[w].firstarc;p;p=p->nextarc)
{
k=p->adjvex;
if(!visited[k])
{
visited[k]=true;
cout<<vertices[k].data<<" ";
qu.push(k);
}
}
}
}
void Print_X_Y_Path(int u,int v,int l,int d)
{
//求出一条长度为l的从u到v的路径,d刚进来的时候是-1
int m;
d++;
visited[u]=true;
path[d]=u;
if(u == v && d == l) //找到一条路径
{
for(int i=0;i<l;i++)
cout<<vertices[ path[i] ].data<<"-->";
cout<<vertices[ path[i] ].data<<endl;
}
else if(u == v && d!=l)
{
//出现这种情况直接回溯上一顶点,不浪费时间去DFS
goto loop;
}
else
{
ArcNode *p=vertices[u].firstarc; //继续DFS
while(p)
{
m=p->adjvex;
if(!visited[m])
Print_X_Y_Path(m,v,l,d);
p=p->nextarc;
}
}
//恢复环境,使顶点可重新使用
//路径长度减一
loop: visited[u]=false;
d--;
}
void Print_X_X_Path(int i,int j,int d)
{
//找出从i到i的回路,思想和上面的类似
int v,k;
ArcNode *p;
visited[i]=true;
d++;
path[d]=i;
if(i == j && d>2)
{
for(k=0;k<d;k++)
cout<<vertices[ path[k] ].data<<"-->";
cout<<vertices[ path[k] ].data<<endl;
}
else if(i == j && d==2) //一条边只可以走一次
goto lop;
else
{
p=vertices[i].firstarc;
while(p)
{
v=p->adjvex;
if(!visited[v] || v == j)
Print_X_X_Path(v,j,d);
p=p->nextarc;
}
}
lop: visited[i]=false;
d--;
}
};主函数文件
#include "graph.h"
#include <iostream>
#include <string>
using namespace std;
int main()
{
NDGraph G;
string v1,v2;
int u,v;
int num;
G.Create_NDGraph();
cout<<"图的深度优先遍历为:";
G.DFS_Traverse();
cout<<endl;
cout<<"图的广度优先遍历为:";
G.BFS_Traverse();
cout<<endl;
cout<<"输入两个顶点名称和一个数字,"<<endl;
cout<<"将输出长度为输入数字大小的两顶点间路径:";
cin>>v1>>v2>>num;
u=G.Locate_Vex(v1);
v=G.Locate_Vex(v2);
if(u == -1 || v == -1)
{
cout<<"顶点中有不符合要求的,操作失败"<<endl;
}
else
{
for(int i=0;i<G.GetVexNum();i++)
visited[i]=false;
cout<<"顶点 "<<v1<<" 到 "<<v2<<" 长度为 "<<num<<" 的简单路径如下:"<<endl;
G.Print_X_Y_Path(u,v,num,-1);
}
cout<<"输入一个顶点名称,将输出所有经过它的回路:";
cin>>v1;
u=G.Locate_Vex(v1);
if(u == -1)
{
cout<<"顶点不存在,操作失败"<<endl;
}
else
{
for(v=0;v<G.GetVexNum();v++)
visited[v]=false;
cout<<"经过顶点 "<<v1<<" 的所有回路如下:"<<endl;
G.Print_X_X_Path(u,u,-1);
}
return 0;
}测试结果:
输入顶点数和边数:5 6
输入顶点名称:v1 v2 v3 v4 v5
输入每条边对应的两个顶点:v1 v2
输入每条边对应的两个顶点:v1 v4
输入每条边对应的两个顶点:v2 v4
输入每条边对应的两个顶点:v2 v3
输入每条边对应的两个顶点:v3 v5
输入每条边对应的两个顶点:v4 v5
无向图构造完成
图的深度优先遍历为:v1 v4 v5 v3 v2
图的广度优先遍历为:v1 v4 v2 v5 v3
输入两个顶点名称和一个数字,
将输出长度为输入数字大小的两顶点间路径:v1 v3 3
顶点 v1 到 v3 长度为 3 的简单路径如下:
v1-->v4-->v5-->v3
v1-->v4-->v2-->v3
输入一个顶点名称,将输出所有经过它的回路:v4
经过顶点 v4 的所有回路如下:
v4-->v5-->v3-->v2-->v4
v4-->v5-->v3-->v2-->v1-->v4
v4-->v2-->v3-->v5-->v4
v4-->v2-->v1-->v4
v4-->v1-->v2-->v3-->v5-->v4
v4-->v1-->v2-->v4
Press any key to continue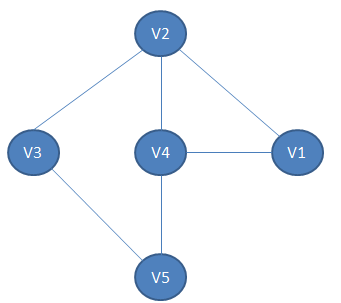
为了更好得理解回溯的过程,可以画画像下面这样的示意图,比如我求 V1 到 V3的长度为3的路径的过程

图可能和你画的不一样,但是主要就是理清一下思路,不会在一重重的递归中乱掉
























 1390
1390

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








