一、前言
就在前天,我抱着紧张的情绪进入了赛场。比赛前看了一遍遍的算法模板,到了比赛的时候却发现很少用到。我自认为二卷的难度是要比一卷简单不少的,考察的算法不多(比如动态规划,DFSBFS),相反,对数学推导、贪心思想、字符串处理考察的更多。但我仍然有一些该AC的题目没能拿全。下面,我来讲部分题目的我的思路,填空第一题和大题第一题都不进行解析,因为这两道题是绝对的签到题,十分简单。事不宜迟,直接开始。
二、题解解析
因为没有找到pdf版本的试卷,这里直接从洛谷上截图了。
(提示:因为官方的题解还没发放且洛谷中的数据不够准确和足够,本文中的代码只有部分能做到AC,没能AC的代码我会讲一下我的思路,欢迎大佬来谈论指点。)
试题B:脉冲强度之和

拿到这道题时,我首先把它看成了规律题,因为p=10*k+45,又要求数位数字相同,我直接认定要求的是从1到2025202的数位上是5的数字总和。但是这里要排除5,因为5不能满足条件1,其次是55555555(不满足条件3)。
public class Main {
public static void main(String[] args) {
long sum = 0;
long p = 0;
for (int n = 1; n <= 8; n++) { // 生成1~8位的全5数字
p = p * 10 + 5;
if (p > 20255202) break; // 超出范围则终止
if ((p - 45) % 10 == 0 && (p - 45) / 10 >= 1) {
sum += p;
}
}
System.out.println(sum); // 输出6172830
}
}试题D:旗帜

这道题我在比赛时用了一个指针遍历“LANQIAO”转换后的字符数组,在遍历矩阵时通过指针做到循环输入。每行结束后,指针额外右移1(模拟题意左移)代码如下:
解法一
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int h = scanner.nextInt();
int w = scanner.nextInt();
char[] pattern = {'L', 'A', 'N', 'G', 'I', 'A', 'O'};
int countA = 0;
int ptr = 0; // 指针初始指向pattern[0]
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
// 填充字符并检查是否为'A'
if (pattern[ptr] == 'A') {
countA++;
}
// 移动指针(循环)
ptr = (ptr + 1) % 7;
}
// 每行起始位置左移1
ptr = (ptr + 1) % 7;
}
System.out.println(countA);
}
}但赛后我又写出一种写法,先看代码:
解法二
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int h = scanner.nextInt();
int w = scanner.nextInt();
String pattern = "LANGIAO";
int countA = 0;
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
int index = (i + j) % 7; // 直接计算字符位置
if (pattern.charAt(index) == 'A') {
countA++;
}
}
}
System.out.println(countA);
}
} 关键在于填充的规律:矩阵中 (i,j) 位置的字符为 pattern[(i + j) % 7]。比如,i和j分别为1,4时,(i+j)%7=5,对应的是'A'。相比之下,这个写法更简单也无需考虑指针转移时可能出现的偏差。
试题E:数列差分

这道题是我的一个重大失误,我在读到题目时,把解题重点放在了如何实现“差分”这个操作,而不是如何求出最小操作数。比赛时在这道题上浪费了很多时间,最后只让代码输出了“1”,大概估测了一下,只能拿到15分。赛后我听其他大佬的解法,排序后用双指针来进行比较,在洛谷上也是直接AC了。代码如下:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Collections;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
Integer[] A = new Integer[n];
Integer[] B = new Integer[n];
// 读取数组A
String[] parts = br.readLine().split(" ");
for (int i = 0; i < n; i++) {
A[i] = Integer.parseInt(parts[i]);
}
// 读取数组B
parts = br.readLine().split(" ");
for (int i = 0; i < n; i++) {
B[i] = Integer.parseInt(parts[i]);
}
// 排序:都按降序排列
Arrays.sort(A, Collections.reverseOrder());
Arrays.sort(B, Collections.reverseOrder());
int ans = 0;
int left = 0, right = n - 1; // left指向A当前最大,right指向A当前最小
for (int j = 0; j < n; j++) {
if (A[left] > B[j]) {
left++; // 匹配成功,移动左指针
} else {
right--; // 用B[j]匹配A的最小元素
ans++; // 需要修改
}
}
System.out.println(ans);
}
}这里简单用了BufferedReader进行了快读。其中,left指针指向A中当前最大的元素,right指针指向A中当前最小的元素。如果A[left]>B[j],则直接匹配;否则就用B[j]去匹配A[right],并移动right指针,且要增加操作次数。
这里的贪心策略为:总是尝试用最大的B去匹配最大的A,如果不能匹配则用最小的A。
试题F:基因配对

这道题我在比赛时因为没有思路直接跳过了,虽然这道题没写出来,但下面的“栈与乘积”我做了出来。所以说,在比赛时我认为在必要时是要做取舍的,不能在一道自己毫无思路的题上浪费太多时间。赛后我也查看了其他大佬的思路,发现使用滑动窗口+哈希表这个思路非常棒,输入案例得到的输出也正确,不过我这里洛谷不知为何卡住了,没办法提交这个答案,有人想知道通过率的话可以试着提交一下。
mport java.util.Scanner;
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String s = sc.next();
int n = s.length();
// 用于统计有效配对的数量,初始化为0
long count = 0;
// 限制最大子串长度,防止内存溢出(MLE),取字符串长度和20中的较小值
int maxLen = Math.min(20, n);
// 预处理:存储每个子串及其反转子串的出现位置
// key为子串,value为该子串在原字符串中出现的起始位置的列表
Map<String, List<Integer>> substrPos = new HashMap<>();
// 枚举子串的长度,从1到最大长度maxLen
for (int len = 1; len <= maxLen; len++) {
// 枚举子串的起始位置,确保子串不越界
for (int i = 0; i + len <= n; i++) {
// 截取长度为len的子串
String sub = s.substring(i, i + len);
// 生成子串的反转子串(0变为1,1变为0)
String reversed = reverseBits(sub);
// 将子串及其出现位置存入map中,如果子串不存在则创建一个新的列表
substrPos.computeIfAbsent(sub, k -> new ArrayList<>()).add(i);
// 将反转子串及其出现位置存入map中,如果反转子串不存在则创建一个新的列表
substrPos.computeIfAbsent(reversed, k -> new ArrayList<>()).add(i);
}
}
// 滑动窗口统计有效配对
// 再次枚举子串的长度,从1到最大长度maxLen
for (int len = 1; len <= maxLen; len++) {
// 再次枚举子串的起始位置,确保子串不越界
for (int i = 0; i + len <= n; i++) {
// 截取当前的子串
String current = s.substring(i, i + len);
// 获取当前子串在原字符串中出现的起始位置的列表
List<Integer> positions = substrPos.get(current);
if (positions != null) {
// 当前窗口结束位置
int endPos = i + len - 1;
// 二分查找第一个起始位置 > endPos的索引
int left = 0, right = positions.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (positions.get(mid) > endPos) {
right = mid;
} else {
left = mid + 1;
}
}
// 统计有效配对的数量,即当前子串在当前窗口之后出现的次数
count += positions.size() - left;
}
}
}
// 输出有效配对的数量
System.out.println(count);
}
// 反转01字符串的方法
private static String reverseBits(String s) {
StringBuilder sb = new StringBuilder();
// 遍历字符串中的每个字符
for (char c : s.toCharArray()) {
// 如果字符为0则转换为1,否则转换为0
sb.append(c == '0' ? '1' : '0');
}
// 返回反转后的字符串
return sb.toString();
}
}
试题G:栈与乘积

这道题我当开始用的是java自带的Stack,但写到第三步的时候我发现,实现累乘操作的话比较麻烦,所以我又改成了模拟栈,前两步都没问题,第三步直接用的遍历,当时没有想太多,现在想想可能会超时。不过拿到90分应该是没有问题。赛后我又进行了简单的优化,每次累乘之后判断是否溢出,这样就可以提前结束,更有可能拿到满分。
这段代码中也使用了快读来处理大数据输入。
import java.util.*;
import java.io.*;
public class Main {
// 定义一个常量 MAX,其值为 2 的 32 次方,用于判断栈中元素乘积是否溢出
static final long MAX = 1L << 32;
public static void main(String[] args) throws IOException {
// 创建一个 BufferedReader 对象,用于从标准输入读取数据
// 使用 InputStreamReader 将字节流转换为字符流,以处理文本输入
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 读取第一行输入并将其转换为整数,此整数表示操作的总次数
int Q = Integer.parseInt(br.readLine());
// 创建一个长度为 Q 的整型数组 stack,用于模拟栈结构
// Q 代表操作的最大可能次数,因此数组最大可能空间为 Q
int[] stack = new int[Q];
// 定义一个整型变量 top 作为栈顶指针,初始值为 -1 表示栈为空
int top = -1;
// 循环执行 Q 次操作
while (Q-- > 0) {
// 使用 StringTokenizer 对读取的一行输入进行分割,方便获取不同的操作信息
StringTokenizer st = new StringTokenizer(br.readLine());
// 从分割后的输入中获取第一个标记,并将其转换为整数,得到当前操作的类型
int op = Integer.parseInt(st.nextToken());
// 当操作类型为 1 时,执行入栈操作
if (op == 1) {
// 栈顶指针 top 加 1,指向新的栈顶位置
// 从分割后的输入中获取第二个标记,并将其转换为整数,存入新的栈顶位置
stack[++top] = Integer.parseInt(st.nextToken());
// 当操作类型为 2 时,执行出栈操作
} else if (op == 2) {
// 检查栈是否不为空(即栈顶指针 top 大于等于 0)
if (top >= 0) {
// 若栈不为空,栈顶指针 top 减 1,相当于将栈顶元素弹出
top--;
}
// 当操作类型为 3 时,执行计算栈中前 y 个元素乘积的操作
} else if (op == 3) {
// 从分割后的输入中获取第二个标记,并将其转换为整数,得到要计算乘积的元素个数 y
int y = Integer.parseInt(st.nextToken());
// 检查栈中元素的数量(top + 1)是否小于 y
if (top + 1 < y) {
// 若栈中元素数量不足 y 个,输出 "ERROR" 并跳过本次循环的后续操作
System.out.println("ERROR");
continue;
}
// 初始化一个长整型变量 product 用于存储乘积结果,初始值为 1
long product = 1;
// 定义一个布尔型变量 overflow 用于标记乘积是否溢出,初始值为 false
boolean overflow = false;
// 从栈顶开始,向前遍历 y 个元素
for (int i = top; i > top - y; i--) {
// 将当前元素乘到乘积结果 product 中
product *= stack[i];
// 检查乘积结果 product 是否大于等于 MAX
if (product >= MAX) {
// 若大于等于 MAX,说明乘积溢出,将 overflow 标记为 true 并跳出循环
overflow = true;
break;
}
}
// 根据 overflow 的值输出结果,若为 true 则输出 "OVERFLOW",否则输出乘积结果 product
System.out.println(overflow ? "OVERFLOW" : product);
}
}
}
} 试题H:破解信息
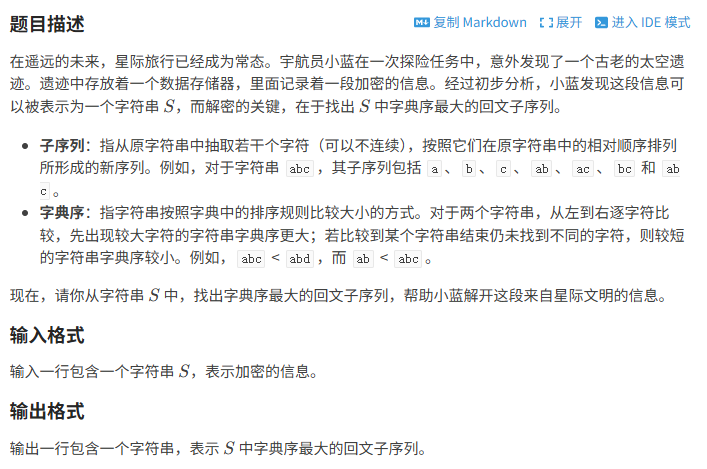
最后这道题我在看的时候是有思路的,刚开始想要使用DFS暴力求解,但当时写到最后脑子已经跟不上了,没能把DFS写出来,最后也只是试着拿了部分分。
先讲一下我刚开始的暴力思路吧。先用DFS枚举出所有的子序列组合,在写一个判断回文序列的函数,最后根据题中条件选出满足条件的字典序最大的回文子序列。代码如下:
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
// 定义一个静态的列表,用于存储所有找到的回文子序列
// 因为后续要在所有回文子序列中找出字典序最大的,所以先将它们都存起来
private static List<String> palindromicSubsequences = new ArrayList<>();
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String s = scanner.next();
// 调用深度优先搜索方法 dfs 开始生成所有可能的子序列,并筛选出回文子序列
dfs(s, 0, "");
// 初始化一个空字符串,用于存储最终找到的字典序最大的回文子序列
String maxPalindrome = "";
// 遍历存储所有回文子序列的列表
for (String palindrome : palindromicSubsequences) {
// 使用 compareTo 方法比较当前回文子序列和已记录的最大回文子序列的字典序
// 如果当前回文子序列的字典序更大,则更新最大回文子序列
if (palindrome.compareTo(maxPalindrome) > 0) {
maxPalindrome = palindrome;
}
}
// 输出最终找到的字典序最大的回文子序列
System.out.println(maxPalindrome);
}
// 深度优先搜索方法,用于生成字符串 s 的所有子序列,并将其中的回文子序列添加到列表中
// s 是原始字符串,index 是当前处理到的字符索引,current 是当前已经生成的子序列
private static void dfs(String s, int index, String current) {
// 当索引等于字符串的长度时,说明已经处理完了所有字符
if (index == s.length()) {
// 检查当前生成的子序列是否为回文序列
if (isPalindrome(current)) {
// 如果是回文序列,则将其添加到存储回文子序列的列表中
palindromicSubsequences.add(current);
}
// 结束当前递归调用
return;
}
// 情况一:不选择当前索引对应的字符,继续处理下一个字符
dfs(s, index + 1, current);
// 情况二:选择当前索引对应的字符,添加到当前子序列中,并继续处理下一个字符
dfs(s, index + 1, current + s.charAt(index));
}
// 判断一个字符串是否为回文序列的方法
private static boolean isPalindrome(String s) {
// 初始化左指针,指向字符串的起始位置
int left = 0;
// 初始化右指针,指向字符串的末尾位置
int right = s.length() - 1;
// 当左指针小于右指针时,继续比较字符
while (left < right) {
// 如果左右指针指向的字符不相等,说明该字符串不是回文序列
if (s.charAt(left) != s.charAt(right)) {
return false;
}
// 左指针右移一位
left++;
// 右指针左移一位
right--;
}
// 如果循环结束都没有发现不相等的字符,说明该字符串是回文序列
return true;
}
} 后来我又想到一种很简单的思路,真的很简单很简单!不废话,直接看代码:
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String s = scanner.next();
// 初始化一个字符变量 maxChar,用于存储字符串 s 中字典序最大的字符,初始值设为 'a'
char maxChar = 'a';
// 遍历字符串 s 中的每个字符
for (char c : s.toCharArray()) {
// 如果当前字符 c 的字典序大于 maxChar,则更新 maxChar 的值为 c
if (c > maxChar) {
maxChar = c;
}
}
// 初始化一个整数变量 count,用于统计字符串 s 中字典序最大字符的出现次数,初始值为 0
int count = 0;
// 再次遍历字符串 s 中的每个字符
for (char c : s.toCharArray()) {
// 如果当前字符 c 等于字典序最大的字符 maxChar,则将计数器 count 加 1
if (c == maxChar) {
count++;
}
}
// 输出由字典序最大的字符重复 count 次组成的字符串,该字符串即为字典序最大的回文子序列
System.out.println(String.valueOf(maxChar).repeat(count));
}
}
没错,用的就是贪心思想。要使整个回文子序列的字典序最大,就应该选择最大的字符,又已知全由相同字符组成的字符串必然是回文,所以最长且全由最大字符组成的回文子序列,就是最优解。因此,只需统计字符串中字典序最大的字符,并全部选取即可。
三、赛后总结
在本次竞赛的征程中,二卷试题虽未呈现出令人望而却步的高难度,但其背后更多的是对思维深度与心态把控的考验。于赛场之上,紧张的情绪恰似绊脚之石,会扰乱清晰的思路;而在难题上的过度执着,亦如深陷迷雾的徘徊,消耗着宝贵的时间与精力。
既然比赛结束了,就不该再有太多的顾虑,认真复盘,放松心情才是赛后该做的事。一次失利不代表努力白费,日后多加磨炼必能造就自己的成功!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








