本文主要对机器学习中常用的两种正则化技术 L1/L2 regularization 进行介绍
正则化技术可以说是一种对模型复杂度进行限制的方法,假设我们的hypothesis space为 F \mathcal F F,模型为 f f f,模型复杂度为 Ω ( f ) \Omega(f) Ω(f), Ω \Omega Ω是一个从 F \mathcal F F到 R ≥ 0 R^{\geq 0} R≥0(指大于等于0的实数)的映射。
所以在之前Constrained ERM的基础上,考虑正则化之后,出现了下面的表达,
Constrained ERM - Ivanov regularization (对模型复杂度的限制作为优化的约束条件)
m i n f ∈ F 1 n Σ i = 1 n l ( f ( x i ) , y i ) min_{f\in\mathcal F}\frac{1}{n}\Sigma_{i=1}^nl(f(x_i), y_i) minf∈Fn1Σi=1nl(f(xi),yi) s . t . Ω ( f ) ≤ r s.t.\ \Omega(f)\leq r s.t. Ω(f)≤r
下面是penalized版本。
Penalized ERM - Tikhonov regularization (对模型复杂度的限制加入到优化目标中)
m i n f ∈ F 1 n Σ i = 1 n l ( f ( x i ) , y i ) + λ Ω ( f ) min_{f\in \mathcal F}\frac{1}{n}\Sigma_{i=1}^nl(f(x_i), y_i)+\lambda \Omega(f) minf∈Fn1Σi=1nl(f(xi),yi)+λΩ(f)
在很多情形下,上述的两种正则化方法可以给出相同的结果。
了解了正则化的一般形式之后,下面以线性回归为例介绍L1/L2 regularization(以penalized版本为例)。
Ridge Regression (L2)
w ^ = a r g m i n w ∈ R d 1 n Σ n = 1 n ( w T x i − y i ) 2 + λ ∣ ∣ w ∣ ∣ 2 2 \widehat w=argmin_{w\in R^d}\frac{1}{n}\Sigma_{n=1}^n(w^Tx_i-y_i)^2+\lambda ||w||_2^2 w =argminw∈Rdn1Σn=1n(wTxi−yi)2+λ∣∣w∣∣22
Lasso Regression (L1)
w ^ = a r g m i n w ∈ R d 1 n Σ n = 1 n ( w T x i − y i ) 2 + λ ∣ ∣ w ∣ ∣ 1 \widehat w=argmin_{w\in R^d}\frac{1}{n}\Sigma_{n=1}^n(w^Tx_i-y_i)^2+\lambda ||w||_1 w =argminw∈Rdn1Σn=1n(wTxi−yi)2+λ∣∣w∣∣1
那么L1/L2 regularization有什么区别呢?大家都知道,区别主要是在于L1 regularization会带来权重的sparsity,也就是有一些权重会是0。那么为什么会有这个结果呢?
先看一下下面这两幅图,这个是用funding,not-hs,college4,college以及hs这5个特征用linear regression去拟合一个target变量,随着正则化程度的降低(也就是x轴从左到右),linear model的各个特征对应的系数的变化情况。
所以通过对比确实可以发现Lasso相对于Ridge有系数直接置为0的特点。

相信这张图大家看到应该都不陌生,这是一般在讲到L1的sparsity的时候都会用的图,那么这个图怎么看怎么理解呢?
首先,假设我们的特征是2维的,那么我们的hypothesis space F \mathcal F F可以表示为 F = { f ( x ) = β 1 x 1 + β 2 x 2 } \mathcal F=\{ f(x)=\beta_1x_1+\beta_2x_2\} F={f(x)=β1x1+β2x2},可视化为 { ( β 1 , β 2 ) ∈ R 2 } \{(\beta_1, \beta_2)\in R^2\} {(β1,β2)∈R2},也就是2-D平面内的每一个点现在代码一个linear function。所以下图左右的蓝色部分分别表示L1-norm和L2-norm的等高线(参考上述的Ivanov regularization形式)。而具有sparsity的linear model,就是在坐标轴上的点。
下图中的 β ^ \hat\beta β^表示什么呢,表示的是没有正则化项存在时,Constrained ERM求到的解。而我们可以发现这个解显然不满足我们的正则化约束条件,所以现在的任务就是要找一个满足约束条件,并且可以使Empirical Risk尽可能小的点。
于是绘制Empirical Risk的等高线图,因为 x 1 x_1 x1和 x 2 x_2 x2的数据大小尺度不一定相同的原因,所以等高线是椭圆,当误差等高线与正则化项等高线第一次有交点时,我们就找到了我们想找的点了,因为一个点表示一个linear model,所以也就是找到了我们想要的model。

因为L1相比于L2,交点更容易出现在坐标轴上,所以L1-regularization更会产生sparsity。该课程的教授提出了一种比较直观的考虑方式,如下图所示,

蓝色区域是L1-norm的等高线,为了方便考虑,我们现在假设Empirical Risk的等高线图为正圆,那么只要
β
^
\hat\beta
β^在黄色区域的时候,交点就会出现在坐标轴上,所以可以发现L1有较大的几率出现sparsity的可能。
L1 & L2 & Elastic Net
考虑这样一种情形,数据只有一维特征 x 1 x_1 x1,然后通过ERM,求得 f ( x ) = 4 x 1 f(x)=4x_1 f(x)=4x1,现在新增一列新特征 x 2 x_2 x2,假设 x 1 = x 2 x_1=x_2 x1=x2,那么通过ERM可以得到 f ( x ) = w 1 x 1 + w 2 x 2 f(x)=w_1x_1+w_2x_2 f(x)=w1x1+w2x2,满足 w 1 + w 2 = 4 w_1+w_2=4 w1+w2=4就行。
然后考虑加上正则化的情形,如下图所示。
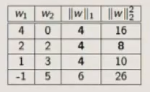
所以可以发现,当特征完全相同的时候,L1正则化会保证这些
w
e
i
g
h
t
s
weights
weights同号,但是对具体值不管;L2正则化会使这些
w
e
i
g
h
t
s
weights
weights相同。
Elastic Net 是L1与L2的结合,因为L1对相同/强相关特征的 w e i g h t s weights weights具体值不管,而为了减小误差( 类似于多次测量求平均值减小误差的想法 ),我们可能往往会希望这些特征的权重会相似,所以在L1的基础上,稍微加上一些L2
w ^ = a r g m i n w ∈ R d 1 n Σ n = 1 n ( w T x i − y i ) 2 + λ 1 ∣ ∣ w ∣ ∣ 1 + λ 2 ∣ ∣ w ∣ ∣ 2 2 \widehat w=argmin_{w\in R^d}\frac{1}{n}\Sigma_{n=1}^n(w^Tx_i-y_i)^2+\lambda_1 ||w||_1 + \lambda_2 ||w||_2^2 w =argminw∈Rdn1Σn=1n(wTxi−yi)2+λ1∣∣w∣∣1+λ2∣∣w∣∣22
Lasso 的正则化系数
在建模过程中,我们的正则化系数相当于我们模型的超参数,需要我们人为设置与调整,所以如果有一些规则可以减小我们的搜索范围,当然是比较有用处的。
对于 Lasso regression,objective function为
L ( w ) = ∣ ∣ X w + b − y ∣ ∣ 2 2 + λ ∣ ∣ w ∣ ∣ 1 L(w)=||Xw+b-y||_2^2+\lambda ||w||_1 L(w)=∣∣Xw+b−y∣∣22+λ∣∣w∣∣1
( 把 coefficient 与 bias 分开了)
对于
λ
>
λ
m
a
x
=
2
∣
∣
X
T
(
y
−
y
ˉ
)
∣
∣
∞
\lambda > \lambda_{max}=2||X^T(y-\bar y)||_{\infty}
λ>λmax=2∣∣XT(y−yˉ)∣∣∞,coefficient
w
w
w为0。(
y
^
\hat y
y^为
y
y
y的均值 )
证明过程如下:
假设 w ∗ = 0 w^*=0 w∗=0 minimize L ( w ) L(w) L(w),因为 L ( w ) L(w) L(w)对 w w w是凸的,所以
L ( 0 , v ) = l i m h → 0 + L ( v h ) − L ( 0 ) h ≥ 0 L(0, v)=lim_{h\rightarrow 0^+}\frac{L(vh)-L(0)}{h}\geq 0 L(0,v)=limh→0+hL(vh)−L(0)≥0
即,从任何方向 v v v逼近 w ∗ w^* w∗的导数都小于等于0。
反之也成立,如果满足从任何方向 v v v逼近 w ∗ w^* w∗的导数都小于等于0, w ∗ w^* w∗为minimizer。
令 b − y = − y ′ b-y=-y' b−y=−y′,解上式得到,
L ( 0 , v ) = − 2 ( v T X T y ′ ) + λ ∣ ∣ v ∣ ∣ 1 ≥ 0 L(0,v)=-2(v^TX^Ty')+\lambda ||v||_1 \geq 0 L(0,v)=−2(vTXTy′)+λ∣∣v∣∣1≥0
即, λ ≥ 2 v T X T y ′ ∣ ∣ v ∣ ∣ 1 \lambda \geq \frac{2v^TX^Ty'}{||v||_1} λ≥∣∣v∣∣12vTXTy′
因为 v T X T y ′ ∣ ∣ v ∣ ∣ 1 ≤ ∣ ∣ X T y ′ ∣ ∣ ∞ Σ v T ∣ ∣ v ∣ ∣ 1 ≤ ∣ ∣ X T y ′ ∣ ∣ ∞ \frac{v^TX^Ty'}{||v||_1}\leq||X^Ty'||_{\infty}\frac{\Sigma v^T}{||v||_1}\leq||X^Ty'||_{\infty} ∣∣v∣∣1vTXTy′≤∣∣XTy′∣∣∞∣∣v∣∣1ΣvT≤∣∣XTy′∣∣∞
所以 ∣ ∣ X T y ′ ∣ ∣ ∞ ||X^Ty'||_{\infty} ∣∣XTy′∣∣∞是 λ \lambda λ下界的上限,当 λ > 2 ∣ ∣ X T y ′ ∣ ∣ ∞ \lambda > 2||X^Ty'||_{\infty} λ>2∣∣XTy′∣∣∞时,使得 w ∗ = 0 w^*=0 w∗=0。
当 w = 0 w=0 w=0时, L ( 0 ) = ∣ ∣ b − y ∣ ∣ 2 2 L(0)=||b-y||_2^2 L(0)=∣∣b−y∣∣22, b = y ˉ b=\bar y b=yˉ使得 L ( 0 ) L(0) L(0)最小。
所以综上, λ > λ m a x = 2 ∣ ∣ X T ( y − y ˉ ) ∣ ∣ ∞ \lambda > \lambda_{max}=2||X^T(y-\bar y)||_{\infty} λ>λmax=2∣∣XT(y−yˉ)∣∣∞时, w ∗ = 0 w^*=0 w∗=0。
参考资料:NYU 《Machine Learning》 2016






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








