从公式解析RNN的梯度消失与爆炸：根源与机制-CSDN博客

本文链接：https://blog.csdn.net/jsntghf/article/details/148540309

循环神经网络(RNN)因其处理序列数据的能力而备受关注，但其训练过程中普遍存在的梯度消失(Vanishing Gradients)和梯度爆炸(Exploding Gradients)问题严重制约了模型性能（扩展阅读：初探注意力机制-CSDN博客）。本文旨在从数学公式的角度，深入剖析这些问题的产生机制。通过解析RNN前向传播和反向传播的数学表达式，我们将揭示梯度不稳定性的根本原因，阐明权重矩阵在其中的关键作用，并探讨这些现象对模型学习长期依赖关系的影响。这一分析不仅有助于理解RNN的固有局限性，也为后续改进架构(如LSTM、GRU)的设计原理提供了理论基础。

RNN基本结构与时间展开

循环神经网络的核心特征是其隐藏状态的循环连接，这使得网络能够保持对历史信息的记忆。从数学角度看，RNN在时间步 $t$ 的隐藏状态 $h_t$ 可表示为：

$h_t = \sigma(W_{hh} h_{t-1} + W_{xh} x_t + b_h)$

其中 $W_\text{hh}$ 是隐藏层到隐藏层的权重矩阵， $W_\text{xh}$ 是输入到隐藏层的权重矩阵， $b_h$ 是偏置项， $\sigma$ 是非线性激活函数(通常为tanh或ReLU)。

为分析梯度传播，我们需要将RNN沿时间轴展开，形成一个等效的深度前馈网络。对于一个长度为 $T$ 的序列，展开后的网络将有 $T$ 层，每层对应一个时间步。这种展开揭示了RNN处理序列数据的本质：通过共享参数在时间维度上的重复应用。

展开后的计算图显示，梯度需要通过所有时间步反向传播，这使得梯度信号可能随着传播距离的增加而指数级地放大或缩小。特别地，隐藏状态之间的递归关系意味着 $W_\text{hh}$ 矩阵将在梯度计算中被反复相乘，这是导致梯度不稳定性的关键因素。

梯度传播的数学推导

RNN 前向传播公式

设 RNN 的隐藏状态更新公式为：

$h_t = \sigma(W_{hh} h_{t-1} + W_{xh} x_t + b_h)$

其中：

$h_{t} \in \mathbb{R}^d$ 是时间步 $t$ 的隐藏状态
$W_{hh} \in \mathbb{R}^{d \times d}$ 是隐藏层权重矩阵
$W_{xh} \in \mathbb{R}^{d \times m}$ 是输入层权重矩阵
$\sigma(\cdot)$ 是激活函数（通常为 tanh 或 ReLU）

时间展开计算图

RNN 可以沿时间轴展开 $T$ 步，形成类似深度前馈网络的结构：

$h_1 = \sigma(W_{hh} h_0 + W_{xh} x_1 + b_h) \\ h_2 = \sigma(W_{hh} h_1 + W_{xh} x_2 + b_h) \\ \vdots \\ h_T = \sigma(W_{hh} h_{T-1} + W_{xh} x_T + b_h)$

由于 RNN 是参数共享的，所有时间步共享相同的 $W_{hh}$ ，这使得梯度计算涉及 $W_{hh}$ 的多次连乘。

反向传播梯度计算

假设损失函数 $L$ 依赖于所有时间步的输出，则梯度 $\frac{\partial L}{\partial W_{hh}}$ 的计算需要沿时间反向传播（BPTT）。

计算 $\frac{\partial L}{\partial h_T}$

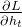首先，计算损失 $L$ 对最后一个隐藏状态 $h_T$ 的梯度： $\frac{\partial L}{\partial h_T}$

计算 $\frac{\partial L}{\partial h_t}$ （递归关系）

对于任意时间步 $t$ ，梯度 $\frac{\partial L}{\partial h_t}$ 不仅依赖于当前步的损失，还依赖于下一步的梯度：

$\frac{\partial L}{\partial h_t} = \left( \frac{\partial h_{t+1}}{\partial h_t} \right)^T \frac{\partial L}{\partial h_{t+1}} + \frac{\partial L}{\partial o_t}$

其中：

$\frac{\partial h_{t+1}}{\partial h_t}$ 是 $h_{t+1}$ 对 $h_t$ 的 Jacobian 矩阵
$\frac{\partial L}{\partial o_t}$ 是当前时间步的损失梯度（通常为 0，除非 $h_t$ 直接用于预测）

计算 Jacobian $\frac{\partial h_{t+1}}{\partial h_t}$

由于 $h_{t+1} = \sigma(W_{hh} h_t + \text{Others})$ ，其 Jacobian 矩阵为：

$\frac{\partial h_{t+1}}{\partial h_t} = W_{hh}^T \cdot \text{diag}(\sigma'(z_t))$

其中：

$z_t=W_{hh}h_{t-1}+W_{xh}x_t+b_h$
$\sigma'(z_t)$ 是激活函数的导数（如 tanh 的导数为 $1 - \tanh^2(z_t) \leq 1$ ）

递归展开梯度计算

从 $t=T$ 到 $t=1$ ，梯度可以递归展开：

$\frac{\partial L}{\partial h_t} =\left( \frac{\partial h_{t+1}}{\partial h_t} \right)^T \frac{\partial L}{\partial h_{t+1}}= \left( W_{hh}^T \text{diag}(\sigma'(z_t)) \right) \frac{\partial L}{\partial h_{t+1}}$

继续展开到 $t=1$ ，得到：

$\frac{\partial L}{\partial h_1} = \left( \prod_{k=1}^{T-1} W_{hh}^T \text{diag}(\sigma'(z_k)) \right) \frac{\partial L}{\partial h_T}$

关键高次幂计算

由于 $W_{hh}$ 在多个时间步共享，梯度计算最终涉及 $W_{hh}$ 的 $T-1$ 次幂：

$\frac{\partial L}{\partial h_1} = \underbrace{ \left( W_{hh}^T \text{diag}(\sigma'(z_1)) \cdot W_{hh}^T \text{diag}(\sigma'(z_2)) \cdots W_{hh}^T \text{diag}(\sigma'(z_{T-1})) \right) }_{\text{High-order product}} \frac{\partial L}{\partial h_T}$

简化分析（忽略 $\sigma'$ 的影响）

假设激活函数导数 $\sigma'(z_k) \approx 1$ ，则梯度近似为：

$\frac{\partial L}{\partial h_1} \approx (W_{hh}^T)^{T-1} \frac{\partial L}{\partial h_T}$

梯度消失/爆炸的条件

梯度爆炸：如果 $W_{hh}$ 的最大特征值 $\lambda max > 1$ ，则 $(W_{hh}^T)^{T-1}$ 会指数增长。
梯度消失：如果 $\lambda max < 1$ ，则 $(W_{hh}^T)^{T-1}$ 会指数衰减。

公式结论

RNN 的梯度计算最终归结为权重矩阵 $W_{hh}$ 的 $T-1$ 次幂：

$\frac{\partial L}{\partial h_1} \approx (W_{hh}^T)^{T-1} \frac{\partial L}{\partial h_T}$

这一高次幂计算使得：

如果 $W_{hh}$ 的特征值 $\left | \lambda \right | > 1$ ，梯度会指数爆炸（Exploding Gradients）。
如果 $\left | \lambda \right | < 1$ ，梯度会指数消失（Vanishing Gradients）。

这就是 RNN 难以训练长序列数据的根本原因！后续的 LSTM、GRU 通过门控机制（避免纯连乘）缓解了这一问题。

完整公式

$\frac{\partial L}{\partial h_1} = \underbrace{ \left( \prod_{k=1}^{T-1} W_{hh}^T \text{diag}(\sigma'(z_k)) \right) }_{\text{Accumulated gradients}} \frac{\partial L}{\partial h_T} \\ \approx \underbrace{ (W_{hh}^T)^{T-1} }_{\text{Weight matrix power}} \frac{\partial L}{\partial h_T}$

代码可视化

权重矩阵连乘效应可视化

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False  # 显示负号

# 设置不同初始权重的矩阵
W1 = np.array([[1.5, 0], [0, 0.5]])   # 最大奇异值>1
W2 = np.array([[0.9, 0], [0, 0.8]])   # 最大奇异值<1

def plot_singular_values(W, ax, title):
    singular_values = []
    for k in range(1, 30):
        W_pow = np.linalg.matrix_power(W, k)
        s = np.linalg.svd(W_pow, compute_uv=False)
        singular_values.append(s[0])
    
    ax.plot(singular_values, 'o-', markersize=4)
    ax.set_title(title, pad=15)
    ax.set_xlabel('矩阵幂次 k')
    ax.set_ylabel('最大奇异值')
    ax.grid(True, linestyle='--', alpha=0.6)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
plot_singular_values(W1, ax1, "梯度爆炸 (σ_max = 1.5 > 1)")
plot_singular_values(W2, ax2, "梯度消失 (σ_max = 0.9 < 1)")
plt.tight_layout()
plt.savefig('weight_singular_values.png', dpi=300, bbox_inches='tight')
plt.show()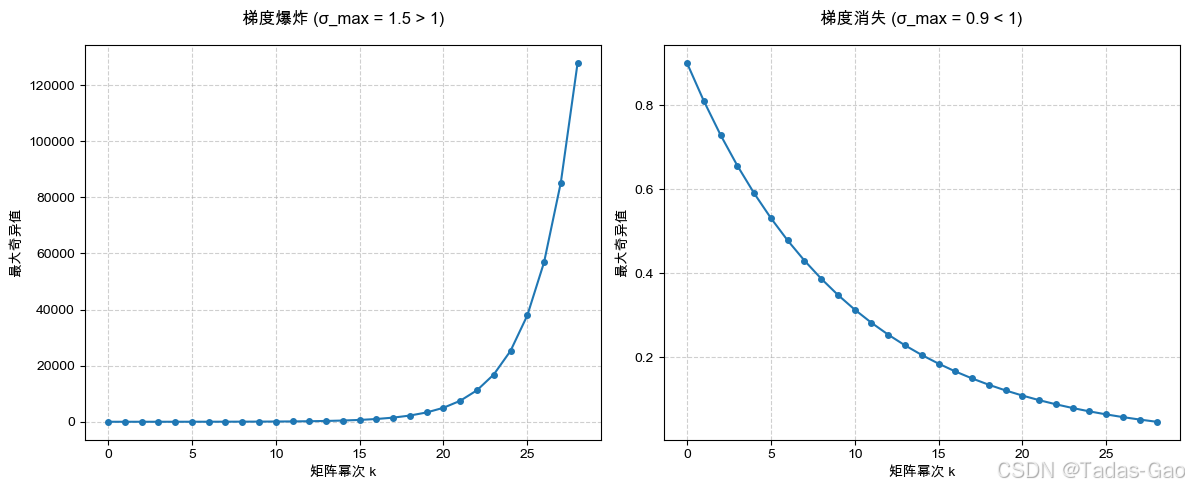

左图展示当权重矩阵最大奇异值大于1时，高次幂会导致数值指数级增长
右图展示当最大奇异值小于1时，高次幂会导致数值指数级衰减

梯度传播计算图

import matplotlib.pyplot as plt
import matplotlib.patches as patches
from matplotlib.path import Path
import numpy as np

plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False

def draw_gradient_flow():
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.set_xlim(0, 10)
    ax.set_ylim(0, 6)
    ax.axis('off')
    
    # 节点定义 (x, y, 名称, 颜色)
    nodes = [
        (2, 4, '输入\n$x$', 'skyblue'),
        (4, 4, '$h_1 = \\sigma(W_1 x)$', 'lightgreen'),
        (6, 4, '$h_2 = \\sigma(W_2 h_1)$', 'lightgreen'),
        (8, 4, '输出\n$\\hat{y}$', 'salmon'),
        (8, 2, '$\\partial L/\\partial \\hat{y}$', 'pink'),
        (6, 2, '$\\partial L/\\partial h_2 = W_3^T \\delta_y \\odot \\sigma\'$', 'pink'),
        (4, 2, '$\\partial L/\\partial h_1 = W_2^T \\delta_{h2} \\odot \\sigma\'$', 'pink'),
        (2, 2, '$\\partial L/\\partial W_1 = x^T \\delta_{h1}$', 'pink')
    ]
    
    # 绘制节点
    for x, y, label, color in nodes:
        ax.add_patch(patches.Rectangle((x-0.8, y-0.4), 1.6, 0.8, 
                      linewidth=1, edgecolor='black', 
                      facecolor=color, alpha=0.7))
        ax.text(x, y, label, ha='center', va='center', fontsize=10)
    
    # 前向传播箭头 (蓝色实线)
    forward_connections = [(0,1), (1,2), (2,3)]
    for i, j in forward_connections:
        ax.annotate("", xytext=(nodes[i][0]+0.8, nodes[i][1]), 
                   xy=(nodes[j][0]-0.8, nodes[j][1]),
                   arrowprops=dict(arrowstyle="->", color="blue", lw=1.5))
    
    # 反向传播箭头 (红色虚线)
    backward_connections = [(3,4), (4,5), (5,6), (6,7)]
    for i, j in backward_connections:
        ax.annotate("", xytext=(nodes[i][0], nodes[i][1]-0.4), 
                   xy=(nodes[j][0], nodes[j][1]+0.4),
                   arrowprops=dict(arrowstyle="->", color="red", 
                                  linestyle="dashed", lw=1.5))
    
    # 添加公式说明
    formula_text = r'$\frac{\partial L}{\partial W_1} = \frac{\partial L}{\partial \hat{y}} \cdot ' \
                   r'\frac{\partial \hat{y}}{\partial h_2} \cdot ' \
                   r'\frac{\partial h_2}{\partial h_1} \cdot ' \
                   r'\frac{\partial h_1}{\partial W_1}$'
    
    ax.text(5, 1, formula_text, ha='center', va='center', 
           fontsize=12, bbox=dict(facecolor='white', alpha=0.8))
    
    # 添加标题和图例
    ax.set_title('神经网络梯度传播计算图', pad=20, fontsize=14)
    ax.plot([], [], 'b-', label='前向传播')
    ax.plot([], [], 'r--', label='反向传播')
    ax.legend(loc='upper right')
    
    plt.tight_layout()
    plt.savefig('gradient_flow_matplotlib.png', dpi=300, bbox_inches='tight')
    plt.show()

draw_gradient_flow()

清晰展示前向传播（蓝线）和反向传播（红线）的数据流
标出关键梯度计算公式

激活函数梯度比较

def plot_activation_gradients():
    x = np.linspace(-3, 3, 100)
    
    # 定义激活函数及其导数
    sigmoid = lambda x: 1/(1+np.exp(-x))
    relu = lambda x: np.maximum(0, x)
    tanh = lambda x: np.tanh(x)
    
    fig, axes = plt.subplots(2, 2, figsize=(12, 10))
    
    # Sigmoid
    axes[0,0].plot(x, sigmoid(x), label='Sigmoid')
    axes[0,0].plot(x, sigmoid(x)*(1-sigmoid(x)), label='导数')
    axes[0,0].set_title("Sigmoid及其导数", pad=10)
    
    # ReLU
    axes[0,1].plot(x, relu(x), label='ReLU')
    axes[0,1].plot(x, (x > 0).astype(float), label='导数')
    axes[0,1].set_title("ReLU及其导数", pad=10)
    
    # 梯度连乘模拟
    layers = 10
    for i, (name, func) in enumerate([('Sigmoid', sigmoid), ('ReLU', relu)]):
        grad_prod = 1
        grads = []
        for _ in range(layers):
            grad = func(x)*(1-func(x)) if name=='Sigmoid' else (x > 0).astype(float)
            grad_prod *= grad
            grads.append(grad_prod)
        
        axes[1,i].plot(x, grads[-1], color='red')
        axes[1,i].set_title(f"{name}梯度连乘({layers}层)", pad=10)
        axes[1,i].set_ylim(-0.1, 1.1)
    
    for ax in axes.flat:
        ax.legend()
        ax.grid(True, linestyle='--', alpha=0.6)
    
    plt.tight_layout()
    plt.savefig('activation_gradients.png', dpi=300)
    plt.show()

plot_activation_gradients()

上排：显示Sigmoid和ReLU的函数曲线及其导数
下排：模拟10层网络中的梯度连乘效果
清晰展示Sigmoid导致的梯度消失问题

梯度监控

import torch
import torch.nn as nn

class SimpleNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(10, 20)
        self.fc2 = nn.Linear(20, 10)
        self.fc3 = nn.Linear(10, 1)
    
    def forward(self, x):
        x = torch.sigmoid(self.fc1(x))
        x = torch.sigmoid(self.fc2(x))
        return self.fc3(x)

def monitor_gradients():
    model = SimpleNN()
    criterion = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
    
    # 模拟数据
    X = torch.randn(100, 10)
    y = torch.randn(100, 1)
    
    grad_history = {name: [] for name, _ in model.named_parameters()}
    
    for epoch in range(100):
        optimizer.zero_grad()
        outputs = model(X)
        loss = criterion(outputs, y)
        loss.backward()
        
        # 记录梯度范数
        for name, param in model.named_parameters():
            if param.grad is not None:
                grad_history[name].append(param.grad.norm().item())
        
        optimizer.step()
    
    # 绘制梯度变化
    plt.figure(figsize=(10, 6))
    for name, grads in grad_history.items():
        plt.semilogy(grads, label=name)
    
    plt.xlabel('训练步数')
    plt.ylabel('梯度范数 (log scale)')
    plt.title('各层梯度范数变化趋势')
    plt.legend()
    plt.grid(True, which="both", ls="--")
    plt.savefig('training_gradients.png', dpi=300)
    plt.show()

monitor_gradients()

显示训练过程中各层梯度范数的变化
使用对数坐标清晰展示梯度消失/爆炸现象
实际训练中可直观发现问题层

梯度消失与爆炸的数学根源

梯度消失和爆炸现象本质上源于权重矩阵 $W_\text{hh}$ 的谱性质。考虑简化情况，忽略非线性激活，则梯度传播可近似为：

$\frac{\partial L}{\partial h_t} \approx (W_{hh}^T)^{T-t} \frac{\partial L}{\partial h_T}$

对 $W_\text{hh}$ 进行特征值分解可知，若其特征值的绝对值普遍小于1，则高次幂将趋近于零(梯度消失)；若存在特征值绝对值大于1，则对应分量将指数增长(梯度爆炸)。

具体而言，假设 $W_\text{hh}$ 的最大奇异值为 $\sigma_{max}$ ，则梯度幅度的变化率将主要取决于 $\sigma_{max}$ ：

当 $\sigma_{max}< 1$ 时，梯度呈指数衰减
当 $\sigma_{max}> 1$ 时，梯度呈指数增长
当 $\sigma_{max}=1$ 时，梯度幅度保持稳定

值得注意的是，即使 $\sigma_{max}$ 略大于或小于1，经过多个时间步的累积后，梯度仍会出现显著的爆炸或消失现象。例如，对于 $\sigma_{max}=1.1$ ，经过100个时间步后将放大约 $1.1^{100} \approx 13780$ 倍；而 $\sigma_{max}=0.9$ 则会缩小至约 $0.9^{100} \approx 0.000026$ 。

与深度前馈网络的对比分析

虽然深度前馈网络也存在梯度消失问题，但RNN的情况更为严重，原因在于：

时间展开深度：RNN的等效深度等于序列长度，可能远大于典型的前馈网络层数
参数共享：相同的 $W_\text{hh}$ 矩阵在多个时间步重复使用，导致梯度计算中的矩阵高次幂
非线性激活：tanh等函数的导数小于1，进一步加剧梯度消失

相比之下，前馈网络中不同层的权重矩阵通常独立，且现代架构使用ReLU、残差连接等技术缓解梯度消失。这些差异使得RNN的梯度不稳定问题更为突出，特别是在处理长序列时。

解决方案的数学原理

针对梯度不稳定问题，研究者提出了多种解决方案，其数学原理如下：

梯度裁剪(Gradient Clipping)：通过限制梯度范数防止爆炸：
$\mathbf{g} \leftarrow \min\left(1, \frac{\theta}{\|\mathbf{g}\|}\right) \cdot \mathbf{g}$
其中 $\theta$ 是预设阈值。这不改变梯度方向，仅控制步长。
精心设计的初始化：如将 $W_\text{hh}$ 初始化为单位矩阵的缩放版，使初始 $\sigma_{max} \approx 1$ 。
使用门控机制(LSTM、GRU)：通过引入门控单元调节梯度流，如LSTM的遗忘门 $f_t$ ：
$C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$
这使得梯度路径包含加性项而非纯连乘，缓解消失问题。
正交初始化：约束 $W_\text{hh}$ 为正交矩阵，保证所有奇异值为1，防止梯度幅度变化。

这些方法从不同角度解决了梯度不稳定性问题，其中门控机制尤为成功，使RNN能够学习更长程的依赖关系。

结论

从公式角度分析，RNN的梯度消失和爆炸问题源于时间展开后权重矩阵的高次幂运算。权重矩阵的谱性质决定了梯度传播的稳定性，而长序列带来的深度放大这一效应。理解这一数学本质不仅解释了传统RNN的局限性，也为改进架构的设计提供了理论指导。门控单元、梯度裁剪等技术通过不同途径缓解了这些问题，使RNN能够更有效地处理长序列数据。未来的研究可进一步探索保持梯度稳定性的新机制，以提升序列模型的长期记忆能力。