逆序对的定义
设有一个序列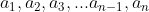 ,对于序列中任意两个元素ai,aj,若i<j,ai>aj,则说明ai和aj是一对逆序对。
,对于序列中任意两个元素ai,aj,若i<j,ai>aj,则说明ai和aj是一对逆序对。
逆序对的几种求法
1.暴力比较:
写两层循环,时间复杂度为
2.归并排序:
众所周知,归并排序就是将一个序列分成两部分进行排序,然后将排序后的两个序列中的元素一个一个插入(如图)
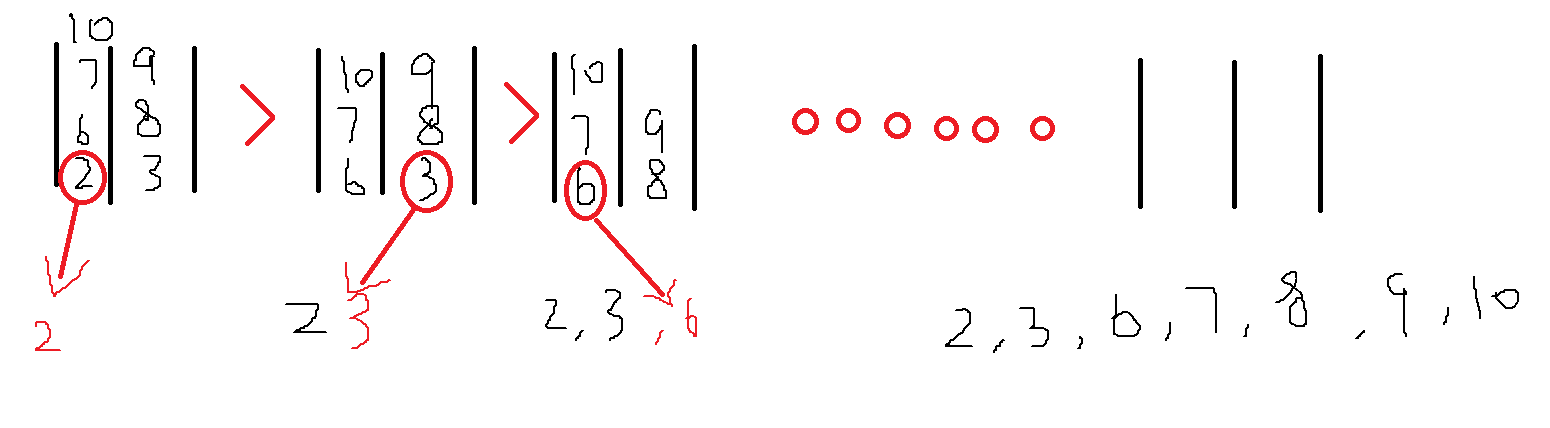
然后,我们发现,对于两个个正在排列的子序列,若后面的子序列中要插入元素,比如上图中要插入3,则前面的子序列中剩下的待排序元素都可以与当前插入的元素组成逆序对(因为前面待排序的元素都比这个元素大,而且下标都比这个元素的下标要小),而且再次递归下去的子序列也是如此。所以程序如下:
#include <iostream>
#include <cstdio>
using namespace std;
int n, a[100005], tmpA[100005], cnt = 0;
void merge_sort(int l, int r, int *A) {
if (l >= r) return ;
int mid = (l + r) >> 1;
merge_sort(l, mid, A);
merge_sort(mid + 1, r, A);
int pl = l, pr = mid + 1, tmpp = 0;
while(pl <= mid && pr <= r) {
if (A[pl] <= A[pr]) tmpA[tmpp++] = A[pl++];
else tmpA[tmpp++] = A[pr++], cnt += mid - pl + 1;
}
while(pl <= mid) tmpA[tmpp++] = A[pl++];
while(pr <= r) tmpA[tmpp++] = A[pr++];
for (int i = 0; i < tmpp; i++) A[i + l] = tmpA[i];
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
merge_sort(1, n, a);
printf("%d\n", cnt);
return 0;
}3.树状数组:
用C(i)表示小于等于i的数的个数,add表示把ai加入C中,更改大于等于ai的C
则求逆序对的算法伪代码如下:
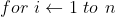
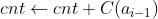
树状数组的操作实现我就不写了,毕竟这不是重点
PS:当序列中的数特别大时,需要使用离散化








 本文介绍了逆序对的基本概念及三种求解方法:暴力比较、归并排序和树状数组。通过实例详细解析了每种方法的具体实现过程及其特点。
本文介绍了逆序对的基本概念及三种求解方法:暴力比较、归并排序和树状数组。通过实例详细解析了每种方法的具体实现过程及其特点。
















 2048
2048

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








