ReLU及其扩展
目前,深度学习中最常见的激活函数是 g(z)=max{0,z} ,翻译为整流线性单元(rectified linear unit)或者称为ReLU。
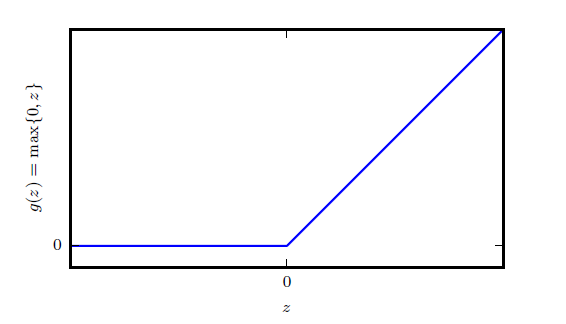
“该激活函数是被推荐用于大多数前馈神经网络的默认激活函数。将此函数用于线性变换的输出将产生非线性变换。然而,函数仍然非常接近线性,在这种意义上它是具有两个线性部分的分段线性函数。由于整流线性单元几乎是线性的,因此它们保留了许多使得线性模型易于使用基于梯度的方法进行优化的属性。它们还保留了许多使得线性模型能够泛化良好的属性。计算机科学的一个公共原则是,我们可以从最小的组件构建复杂的系统。就像图灵机的内存只需要能够存储0 或1 的状态,我们可以从整流线性函数构建一个万能函数近似器。”
以上摘抄自Goodfellow的《深度学习》一书。
ReLU实际上是两段线性函数,当处于激活状态时,它的导数处处为1,保持比较大;但是其在另一半定义域上恒为0,不能通过梯度进行学习。因而有了一些ReLU的扩展函数。
主要有三个:
绝对值整流:固定 αi=−1 使得 g(z)=|z| ;
渗漏整流线性单元(Leaky ReLu):将 αi 固定为类似0.01的小值;
参数化整流线性单元(PReLu):将 αi 作为学习的参数。
sigmoid和tanh
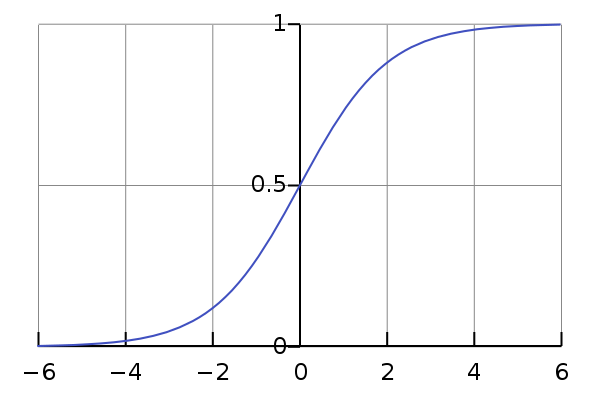
在引入ReLU之前,常用的激活函数是logistic sigmoid函数:
导数为: g′(z)=g(z)(1−g(z))
或者双曲正切函数:
导数为: g′(z)=1−g(z)2
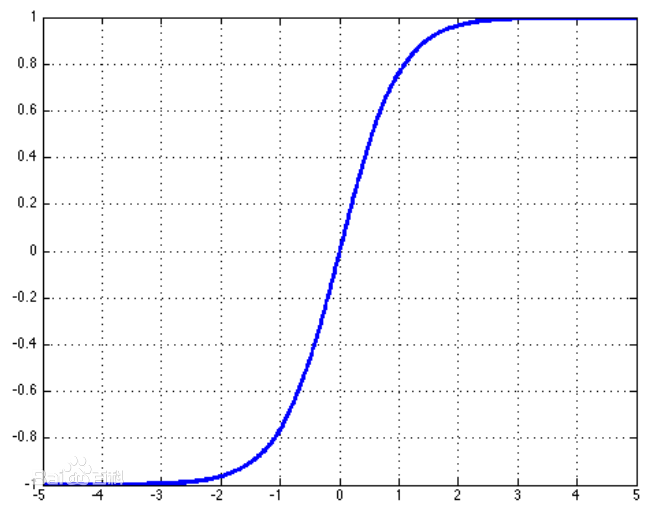
这两个激活函数紧密相关,因为 tanh(z)=2σ(2z)−1 。
当必须要使用sigmoid函数时,tanh函数通常表现的更好,因为tanh更像单位函数,尤其是在0附近时,只要网络的激活能够被保持地很小,训练tanh网络更加容易。
但是这两个函数的广泛饱和性使得基于梯度的学习变得比较困难,一般在CNN中已经很少使用了。
当然还有一些其他的激活函数,比如softplus等,但是如果它们的表现仅仅是跟ReLU大致相当,而不能表现的比ReLU好很多的话,是不会引起其他人的兴趣的。





















 4857
4857











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








