剑指offer_面试题3_二维数组中的查找（简单问题亦不能忽视）

题目：在一个二维数组中，每一行都按照从左到右递增的顺序排序每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样一个二维数组和一个整数，判断数组中是否含有该整数。

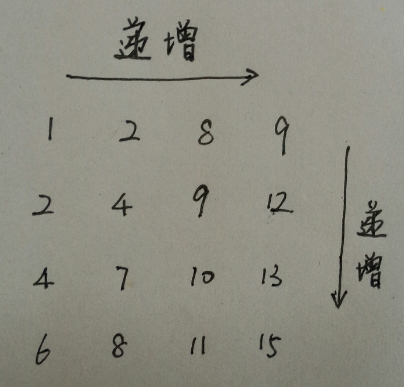
数组如下：

在该数组中查找一个整数隐含的几个规律：

1、在数组中选取一个数，如果与所查目标相等，那么查找结束

2、若所选数字，小于，要查找的目标，则要查找的目标应该在当前选取的位置的右边或者下边

3、若所选数字，大于，要查找的目标，则要查找的目标应该在当前选取的位置的左边或者上边

问题关键如何在该数组中选取整数？

答：在一行中，最右边的数最大；在一列中，最上方的数最小；因此在选数时，就要从此入手。

实例分析：查找目标 7，从右上角选取数字开始

总结上图实例查找过程，规律如下：

1、如果选取数字等于要查找的数字，查找结束

2、如果该数字大于要查找的数字，剔除该数字所在列（因为选取的数字在一列的最上方，已经最小）

3、如果该数字小于要查找的数字，剔除该数字所在行（因为选取的数字在一行的最右边，已经最大）

在了解了以上规律后，开始写代码。在写的过程中我犯了几个错误，或者说找到了 几个知识盲点，在下面一一列举，铭记，共勉。

错误代码一：

下面的代码犯了一个很严重错误，首先编译都过不去。

原因在于 函数传递二维数组时出错，我用的是 a[][]。函数在传递二维数组时，传递的是一个指针的指针，不能省略高维，不然编译器无法正确寻址。应改成 a[][4]。（我设的二维数组为4行4列）

bool Search(int a[][], int number, int rows, int columns)
{
    int i, j;
    int r = rows;
    int c = columns;
    int n = number;

    for(i = 0; i < r;)
    {
        for(j = c - 1; j >= 0;)
        {
            if(a[i][j] == n)
            {
                cout << "找到了，位置在: " << i << ',' << j << endl;
                return true;
            }
            else if(a[i][j] < n){
                i++;
                break;
            }
            else{
                j--;
            }
        }
    }
    cout << "未找到" << endl;
    return false;
}

在改正上面所说的错误后，看似代码可以通过，也可以查找几个数字，比如7，9，15等。但存在很大的不足，没有考虑输入空指针的情况：

不足代码二：

下面的代码改正了上述错误和不足，似乎代码已经完成了，但其实隐藏了一个很大问题，当我用 比数组中最小数字还小的数字测试时，出现死循环。原因就在于两个 for 循环。

由于数字比数组中最小数字还小，因此 表示列的 变量 j，一直减少，直到减到小于0，变成-1，跳出内循环，但 i 不变，导致外层循环不会结束，又重新进入内循环，这样就导致了一个死循环。

（关键是下面的代码，在其他情况，如传递NULL，找二维数组中存在的数字，找大于数组中最大数字的数时都正确，从而让问题很那发现。这一点需要铭记，测试一定要全，最好在写代码前，想好测试用例）

bool Search(int a[][4], int number, int rows, int columns)
{
    int i, j;
    int r = rows;     // 行
    int c = columns;  // 列
    int n = number;   // 要查找的数组

    //一定要加这一段，防止输入空指针，考虑问题要全面
    if(a == NULL || r <= 0 || c <= 0)
    {
        cout << "二维数组有问题" << endl;
        return false;
    }

    for(i = 0; i < r;)
    {
        for(j = c - 1; j >= 0;)
        {
            if(a[i][j] == n)
            {
                cout << "找到了，位置在: " << i << ',' << j << endl;
                return true;
            }
            else if(a[i][j] < n){
                i++;
                break;   // 用于跳出内循环
            }
            else{
                j--;
            }
        }
    }
    cout << "未找到" << endl;
    return false;
}

改进代码三：

下面的代码，改正了上述不足，已能很好达到测试要求。

bool Search(int a[][4], int number, int rows, int columns)
{
    int i, j;
    int r = rows;
    int c = columns;
    int n = number;

    /**一定要加这一段，防止输入空指针，考虑问题要全面*/
    if(a == NULL || r <= 0 || c <= 0)
    {
        cout << "二维数组有问题" << endl;
        return false;
    }

    i = 0;
    j = c - 1;
    while(i < r && j >= 0)
    {
        if(a[i][j] == n)
        {
            cout << "找到了，位置在: " << i << ',' << j << endl;
            return true;
        }
        else if(a[i][j] < n){
            i++;
            // break;
        }
        else{
            j--;
        }
    }

    cout << "未找到" << endl;
    return false;
}

代码三，不属于题目的要求：

主要是因为，我在测试数字 8 时，上述代码只找出了一个 8，还有另外一个位置的 8 未找到，我改进了一下。

bool Search(int a[][4], int number, int rows, int columns)
{
    int i, j;
    int r = rows;
    int c = columns;
    int n = number;

    int k = 0;

    /**一定要加这一段，防止输入空指针，考虑问题要全面*/
    if(a == NULL || r <= 0 || c <= 0)
    {
        cout << "二维数组有问题" << endl;
        return false;
    }
    i = 0;
    j = c - 1;
    while(i < r && j >= 0)
    {
        if(a[i][j] == n)
        {
            cout << "找到了，位置在: " << i << ',' << j << endl;
            k++;
            j--;
            //return true;
        }
        else if(a[i][j] < n){
            i++;
            // break;
        }
        else{
            j--;
        }
    }

    if(k != 0)
        return true;
    else{
        cout << "未找到" << endl;
        return false;
    }
}

主函数如下：

int main()
{
    int a[4][4] = {
        {1,2,8,9},
        {2,4,9,12},
        {4,7,10,13},
        {6,8,11,15}
    };
    Search(a,1,4,4);
    Search(a,15,4,4);

    Search(a,7,4,4);
    Search(a,8,4,4);

    Search(a,0,4,4);
    Search(a,16,4,4);

    Search(NULL,1,4,4);
    return 0;
}

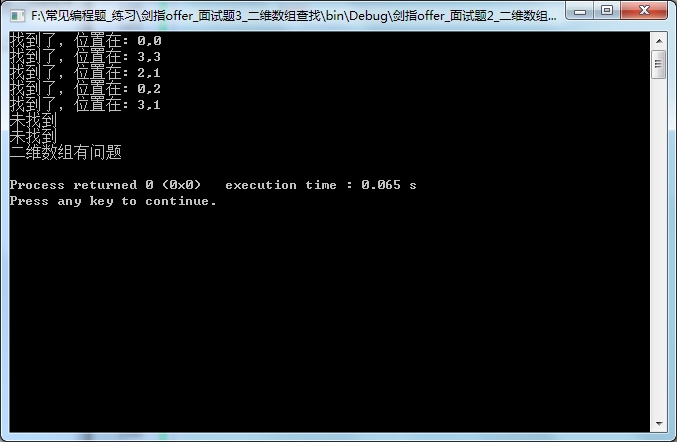
结果图：

/*点滴积累，我的一小步O(∩_∩)O~*/