04. 数学计算

1. 导数

1. 首先在坐标上，x和y有转换计算公式。如 y= x^2 +1 ， 用x的函数表示，f(x ) = x^2 +1 。
2. 导数就是这个坐标曲线在坐标某个点上的斜线率。 直线坐标的斜率就是 = YΔ/ XΔ 。 YΔ 和 XΔ 是 两点上的变化，在直线坐标上的斜率是固定一样的。
3. 曲线坐标中每个点的斜率都是不一样，我们用极限的思想，计算曲线坐标在某个点上的斜率。这个过程叫，计算原函数的导数。
4. 如，原函数是 f(x ) = x^2 +1 , 用f’(x) = x^2 +1 表示，计算原函数的导数。

函数在x0 点上的导数计算表示。 用极限思想，XΔ 接近于0的时候，在x0点上的斜率。

初等函数的导数函数公式:

记住:
（1/x)’ = -(1/x^2)

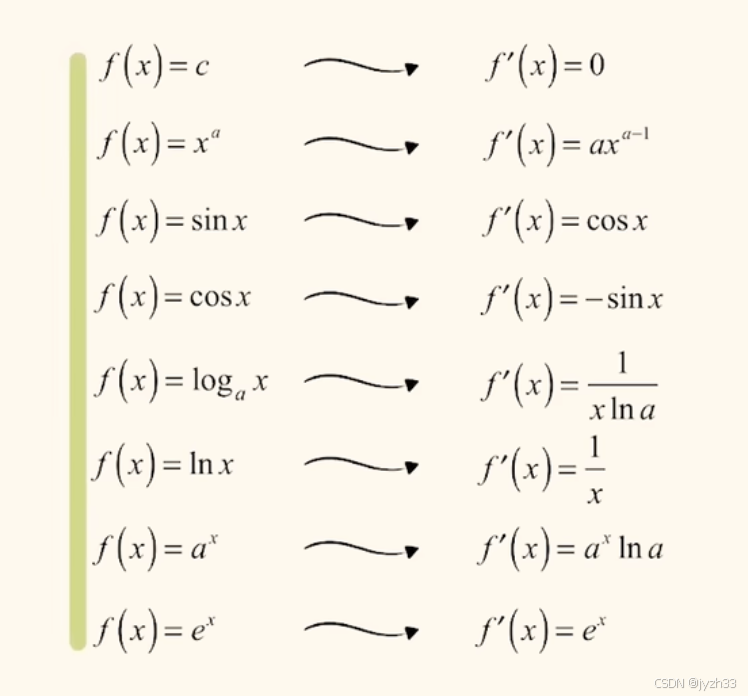
2.根号

X 的 n次方是a ，那X怎么表示 。 X = $\sqrt[n]{a}$ 。
如: $\sqrt[2]{4}$ = 2 , 但是什么的平方是3、5、7等，表示不出来，只能用根号表示，$\sqrt[2]{3}$ 的平方是3 。

根号转幂函数
$\sqrt{x}$ = $x^{\frac{1}{2}}$

$2^3$=8 ， 所以可以这么说 $\sqrt[3]{8}$ = 2

3. 幂函数

$x^n$

4. 指数函数

$a^x$

3. 对数函数

${\log }_{2}8$ 和 ${\log }_{2}7$

$2^3$=8 ， 所以可以这么说， 2为底的8的对手是什么。${\log }_{2}8$ =3

综合:

$\sqrt[3]{8}$ 表示， 什么的 3次方 等于 8 。2的3次方是8，计算2。

${\log }_{2}8$ 表示， 2的几次方是 8。2的3次方是8，计算3。

log与ln

ln和log都是表示对数的符号

ln (自然对数)：
以e为底的对数，记作lnN（N>0）。在自然科学中具有重要意义，特别是在生物学和物理学中。

log (常用对数)：
以10为底的对数，也称为常用对数，能以任何大于0且不等于1的数为底。默认情况下，log表示以10为底的对数。

logN和lnN可以通过以下公式进行转换：

· logN = lnN / ln10
· lnN = logN / loge

公式

log和ln都遵循一定的运算公式：

通用公式

· 积的对数：log(MN) = logM + logN

· 商的对数：log(M/N) = logM - logN

· 幂的对数：log(M^n) = n · logM

· 根的对数：log(√M) = 1/n · logM

log的特殊公式

· 底数转换：log(a)N = log(b)N / log(b)a（b>0且b≠1）

· 指数交换：a^(log(b)N) = N^(log(b)a)

ln的特殊公式

· ln1 = 0

· lne = 1

· ln(MN) = lnM + lnN

· ln(M/N) = lnM - lnN

· ln(M^n) = n · lnM

4. 多远函数的梯度计算

数学中倒三角符号（∇）被称为梯度算子（gradient operator）。读作“梯度”或者“nabla”。
∇f(x,y) 表示多元函数的梯度函数。
在多变量微积分中，梯度是一个向量，其方向指向函数增长最快的方向，其大小（或长度）是该方向上的函数增长速率。

多元函数的梯度计算: