一. 预备代码
#预处理
#导入库
import sklearn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder, OrdinalEncoder
from sklaern.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
#导入数据
df = pd.read_csv('csv_file_path',header=None,names=['col1','col2','col3','col4'])
#定义特征和目标
features = ['col1','col2','col3']
target = 'col4'
#数值特征和分类特征
numeric_features = ['col1']
ordinal_features = ['col2']
onehot_features = ['col3']
#预处理管道
numeric_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='mean')), #填充缺失值
('scaler', StandardScaler()) #数据标准化
])
ordinal_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='most_frequent')),
('ordinal', OrdinalEncoder(categories=[['class1','class2','class3']]))
])
onehot_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='most_frequent')),
('onehot', OneHotEncoder(handle_unknown='ignore'))
])
preprocessor = ColumnTransformer(transforms=[
('num', numeric_transformer, numeric_features),
('ord', ordinal_transformer, ordinal_features),
('onehot', onehot_transformer, onehot_features)
])
#划分训练测试集
X = df[features]
y = df[target]
X_test, X_train, y_test, y_train = train_test_split(X,y,test_size=0.2,random_state=0)
X_train = preprocessor.fit_transform(X_train)
X_test = preprocessor.transform(X_test)
#作图
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(16,6)) #两个子图
ax1.scatter(x1, x2, color='red', marker='x', size=10, label='label_1') #散点图
ax1.set_xlabel('x1')
ax1.set_ylabel('x2')
ax1.set_title('fig1')
X = X.values #转换为numpy
x_min, x_max = X[:,0].min()-1, X[:,0].max()+1 #控制范围
xx = np.linspace(x_min, x_max)
yy = f(xx) #假设yy是关于xx的函数
ax2.plot(xx, yy, color='blue', ls='--', lw=2, label='label_2') #函数图
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_title('fig2')
plt.legend() #显示图例
plt.show()
二. 机器学习基础
1. 机器学习分类
按照任务类型,可以分为监督学习,无监督学习,以及强化学习;
监督学习:
任务:给定样本及其标签,通过数据的特征来预测其标签;
优化目标:最小化预测结果的损失函数(观测值和预测值的偏差大小)
举例:回归/预测问题,分类问题,标注问题,推荐系统
无监督学习:
任务:只给样本不给标签,通过样本的特征找到样本之间的关联
优化目标:使用概率分布建模时,希望最大化数据集的对数似然
举例:聚类问题,概率图模型,PCA,GAN,自编码器
强化学习:
任务:与环境交互,解决决策问题
优化目标:最大化累计回报的期望
举例:人工智能玩游戏
而按照建模方式来分类,可以分为参数化模型和非参数化模型;
参数化模型:
每一个模型都可以用一个具体的参数向量来唯一确定
举例:线性回归,神经网络
非参数化模型:
对数据分布不做先验假设,保留数据本身作为知识,直接在模型空间中寻找实例
举例:Kmeans,KNN,SVM,决策树
2. 机器学习基本概念
2.1 欠拟合与过拟合
欠拟合:
定义:指模型无法拟合出数据中的重要模式
表现:训练损失以及测试损失均较大、
改进:替换模型,增加训练轮数,调整超参数
过拟合:
定义:指模型过度的拟合到了观测数据中不具有普遍性的部分,如噪声
表现:训练损失小而测试损失大
改进:简化模型,加入正则化,早停
2.2 正则化约束
对于参数的复杂度进行约束的方法称为正则化。通过在损失函数中添加惩罚项来约束模型的复杂度,从而达到防止过拟合的效果。
L0正则化:直接惩罚非零特征的数量,但示性函数不可导;
L1正则化(Lasso):实际计算时对于L0的替代;通过惩罚权重的绝对值之和,实现对于模型的稀疏(模型中权重集中在一小部分特征上,其他多数特征变为0)从而简化模型并提高可解释性;适用于高维数据中,帮助自动筛选重要特征;J(θ)=J+λ|θ|
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.1) #alpha控制惩罚力度
lasso.fit(X_train, y_train)
c = lasso.coef_ #回归系数
L2正则化(Ridge):通过惩罚权重的平方和,实现权重平滑,限制了权重的整体规模;适用于对特征进行平滑处理;同时也可以帮助解决特征之间存在的共线性;其也被称为权重衰减法(weight decay),倾向于生成一个在大量特征上均匀分布权重的模型。J(θ)=J+λθ^2
正则化中的λ表示了正则化约束(惩罚)的强度;其越小,能容忍的范数值就越大,最优参数离原点越远。
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
c = riidge.coef_
Elastic Net正则化:结合了L1和L2的正则化模型。
2.3 残差,偏差,与方差
残差:
残差为准确的模型的预测值与真实观测值的差异(例如噪声引起的),若模型可表示为 y=f(x)+epsilon,其中eps即为残差;在一个完美的模型中,残差为满足期望为0的随机噪声
偏差(Bias):
衡量了预测数据集与实际观测集的分散程度
方差(Variance):
衡量了数据集自身内部的离散程度
一个模型在泛化性和灵活性(特征之间的交互作用)之间的基本权衡被描述为偏差-方差均衡(bias-variance tradeoff)
2.4 混淆矩阵
混淆矩阵中的数据是一般分类问题中评价指标的组成部分;以二分类为例:
| 模型预测为正 | 模型预测为负 | |
| 真实标签为正 | TP | FN |
| 真实标签为负 | FP | TN |
其引申出的评价指标如下:
准确率:
在所有样本中预测正确的比例
Accuracy = (TP+TN)/(TP+TN+FP+FN)
精确度:
在所有预测为正的样本中预测正确的比例
Precision = TP/(TP+FP)
召回率【也成为TPR】:
在所有实际标签为正的样本中预测正确的比例
Recall(TPR)= TP/(TP+FN)
相对的,有
FPR = FP/(FP+TN)
F1分数:
为了平衡精确度和召回率,采用他们的调和平均值来衡量
F1 = 2*Precision*Recall/(Precision+Recall)
AUC分数:
衡量模型在不同阈值下的表现;AUC分数为ROC曲线下方的面积,在0.5到1之间,越大越好;
其中ROC曲线是一条在TPR-FPR函数图第一象限中(0,0)到(1,1)之间的一条片偏上方的阶梯状折线图
三. 机器学习基本算法
1. K近邻算法(KNN)
非参数化模型【此处k为需要手动调整的超参数】&监督算法;最基本的分类算法,也能用于回归任务。其通过测量不同特征之间的距离来进行分类或预测。
在分类任务中,先观察与该样本点最近的K个样本(K是需要手动调整的参数),统计这些样本所属的类别,然后将当前样本归到出现次数最多的类中;即:让预测的分类服从邻居中的多数分类。
k值的选择会影响到模型的性能:
k值太小,分类结果容易遭受噪声数据影响;k值太大,可能将远处不相关的样本点包含进来。
一般使用欧氏距离来衡量;若使用其他距离,决策边界会更加尖锐。
以二分类问题为例的核心代码:
from sklearn.neighbors import KNeighborsClassifier as KNC
knc = KNC.fit(X_train,y_train)
acc = knc.score(X_test, y_test) #准确率
以分类平面点集为例的核心代码:
from sklearn.neighbors import KNeighborsClassifier
ks = [1,3,10]
for i,k in enumerate(ks): #enumerate同时返回索引i和值k
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(x_train, y_train)
z = knn.predict(grid_data)
而与分类任务类似,也可以用于回归;首先考虑k个相邻的样本点,将这些样本对应的数值进行加权平均求和,就得到了样本的预测结果;权重代表了不同邻居对于当前样本的重要程度。
2. 线性回归
监督学习算法&参数化模型,用于回归任务;其首先假设数据集中的样本与标签之间存在线性关系,再建立模型求解参数,例如根据特征预测房屋价格;
假设输入为x,模型参数为theta,那么输出就可以写为 theta^T * x ;
训练时的损失函数:选择theta使得MSE均方误差达到最小值(最小二乘法的思想);MSE误差倾向于令模型重点关注与真实偏差差距较大的数据。故其目标即为min∑(yi-f(xi))^2。
由于MSE易于求导,所以常被作为训练时的损失函数;而RMSE由于量纲保持不变,一般用于模型的评价指标。
梯度下降:由于解析解的复杂度太大且求解困难,使用梯度下降法求解参数。为了最小化MSE的值,只需要沿着梯度的反方向即可:更新的参数 = 参数 - 学习率*损失函数对参数的梯度;由于MSE是凸函数,所以无论起点如何,都可以收敛到全局最小值点。
计算参数时的优化:小批量梯度下降MBGD(有时候以SGD代称):将样本随机划分成许多小批量,每次迭代时用一个小批量来计算梯度,以此来估计全样本计算的结果,时间复杂度下降。
训练方法:将一次参数更新称为一步,而将遍历一次所有训练数据称为一轮(epoch)。如果提前设置好轮数,学习率和批量大小,并用梯度下降不断迭代,最后既可以得到数值模拟的近似解。
评估指标:R2分数:;分数在[0.7,1]时可以认为解释能力较强。
核心代码:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
w = model.coef_
b = model.intercept_
y_pred = model.predict(X_test)
r2 = model.score(X_test, y_test) #R2分数
3. 逻辑斯蒂(Logistic)回归
参数化模型;应用在二分类问题中。
基本思想:仍然做线性假设,输入样本与参数进行线性相乘变为 theta^T * x(因此逻辑斯蒂回归也被称为广义线性模型);之后按照阈值大小来指派预测的类别;然而常数阈值有断点不可导,因此采用非线性映射函数映射为概率;最后将样本的类别 y 看做有两个可能值得离散随机变量,将样本经过变换后得到的结果归为概率较大的一类即可。
将样本映射到概率的函数:sigmoid函数 ;总映射为 f(θ) = σ(θ^T*x),这样的模型称为广义线性模型。
优化目标:最大化极大似然估计(MLE);即寻找参数theta使得模型在训练数据上预测出正确标签的概率最大。【似然函数(likelihood):模型将所有样本都预测正确的概率】
评价指标:准确率 Accuracy = (TP+TN)/(TP+TN+FP+FN)以及AUC(ROC曲线[TPR-FPR]下方面积);注意AUC的值事实上与阈值的选取无关。
以平面点集二分类为例的核心代码:
from sklearn.linear_model import LogisticRegression
#ovr表示二分类问题
model = LogisticRegression(solver='liblinear',multi_class='ovr',random_state=0)
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
acc1 = np.mean(y_pred == y_test) #准确率
acc2 = model.score(x_test, y_test) #准确率的另一种写法
y = -model.coef_[0,0]/model.coef_[0,1]*x_test - model.intercept_/model.coef_[0,1] #分割直线
不仅只有二分类,若是多分类则可使用柔性最大值(softmax)函数进行回归映射到多分类概率上,同样输出的是每个样本可能的概率 ;输入时应注意将类编转化为独热编码(若类别平行)或基数编码(若类别有明显的级别之分)。
**交叉熵与似然估计:
从概率分布的角度出发,似然函数即为模型预测正确标签的概率L(θ)=Πf(xi)^yi*(1-f(xi))^(1-yi)【其中f为预测函数σ(θ^Tx),y为标签】;而从信息论的角度,可以衡量预测出的概率分布与实际真实的概率分布的交叉熵的大小。交叉熵衡量了两个概率分布的相似度。在逻辑斯蒂回归中,最大化对数似然函数与最小化交叉熵是等价的。
4. K均值聚类(K-means)
一种无监督学习算法;目标:将样本按照距离划分为数个类。
基本思想:首先随机选取k个样本作为每个类的中心;每个样本被归到离它距离最近的中心点那类中;
在每个类中,计算每类最优的中心点为每个类中所有点的质心;更新质心为中心点后重新计算每个样本到中心点的距离再重新归类;重新归类后再计算新的质心,反复迭代直到预设轮数。
目标函数:簇内点到中心的距离之和;目标函数越好,簇紧密度越高。
其高度依赖于初始中心的选择,可能会陷入局部最优。
以平面点集聚类为例的核心代码:
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4, random_state=42) #聚为四类
kmeans.fit(X)
labels = kmeans.labels_ #每类标签
centroids = kmeans.cluster_centers_ #每类中心
4.1 K-means++算法
为了解决K-means对初始随机中心点过敏感,极易收敛到局部最小值,以及运行时间太长的问题,k-means++算法采用了如下改进:
首先随机选取第一个样本作为第一个聚类的中心点,接下来每次选取中心点时,都有样本x被选为中心点的概率与其到当前中心点距离的平方成反比。也就是说,离现有中心点越远的点越容易被选为新的中心点,解决了原先k-means的问题。
5. 支持向量机(SVM)
监督学习算法,非参数化模型【参数数量与样本数相同】;用于分类和回归任务。其通过寻找最优超平面来最大化数据点到超平面的最小距离,从而进行分类。
平面点集二分类任务:在无数个可以分割这两个点集的超平面中挑选出一个平面,使其与任意一点间隔的最小值最大;将与这样的最优超平面间隔最大的样本点成为支持向量;
在后续的预测中,只需要保留支持向量就可以继续利用模型完成后续的预测任务;若想要用SVM预测某个新样本x的类别时,只需要带入到最优超平面上计算正负性即可。
在数据略微线性不可分的情况下还能增加惩罚项调整软间隔大小,软间隔可以允许一些数据违反边界,有助于处理噪声数据。
5.1 序列最小优化(SMO)算法
由于SVM是非参数化模型,问题的参数数量与数据集规模相当,直接计算不现实;可以采用序列最小优化算法:每次选出两个参数,固定其余的参数,只优化这两个选中的参数保证等式约束一直-
成立;如此反复迭代直到目标函数的值收敛或达到预设轮数为止。事实上,SVM的优化问题是一个复杂的二次规划,而固定其余参数只优化两个参数后优化问题就能够转变为寻找参数的二次函数最大值点。
5.2 核函数(Kernel)
对于线性可分的数据,可以直接使用内积核;内积核相较于直接计算内积能大大节省复杂度;
对于略微线性不可分的数据仍可以使用内积核,同时引入松弛变量;
对于线性不可分的数据,可以引入核函数来对样本升维(将低维数据映射到高维空间),以达到线性可分的效果;常用的核函数为高斯核函数(RBF核),衡量了样本之间基于欧氏距离的相似度;
样本线性可分的核心代码:
from sklearn import svm
model = svm.SVC(kernel='linear')
model.fit(x,y)
w = model.coef_[0]
b = model.intercept_[0]
sv = model.support_vectors_ #支持向量
yy = -(w[0]*xx+b)/w[1] #分割直线
rbf核函数分类的核心代码:【注意sigma越小,gamma越大,决策边界越复杂,越容易出现过拟合】
from sklearn.svm import SVC
model = SVC(kernel='rbf',gamma=50,tol=1e-6) #rbf的参数gamma=1/(2sigma^2)
model.fit(x,y)
Y = model.predict(X)
6. 主成分分析(PCA)
数据降维的无监督学习算法;含义是将高维数据中的主要成分找出来。
主要思想:不断选取数据方差最大的方向作为主成分;如果要将d维的数据降低到k维,只需要计算协方差矩阵最大的k个特征值对应的特征向量即可。
以二维pca为例的核心代码:
from sklearn.decomposition import PCA
X = data[['x1','x2']].values
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
W = pca.components_.T #变换矩阵
7. 决策树
使用了树的结构,通过一系列的规则对数据进行划分,最终形成树状结构,用于预测目标变量;可以用于分类和回归任务;可以组合出非线性分类的效果。
目标:在分类准确率和决策树的复杂度之间寻找平衡;
优化方法:代价函数,最大深度等剪枝方法。
算法:
7.1. ID3算法及C4.5算法
ID3算法从根节点开始每次选取使得信息增益 I(X,Y) 【信息增益即为随机变量X的熵减去在给定Y的分布时X的条件熵。】最大的特征进行分类;缺点:其倾向于无限精细划分,复杂度转移。
而将信息增益改为信息增益率 I_R(X,Y)最大的特征【信息增益率定义为获得的信息增益与Y关于X的复杂度的比值。】来抑制无限精细划分导致的过拟合,就变为C4.5算法。
另外,为了防止ID3算法构造出非常长的分支,还可以使用决策树的代价函数来惩罚叶节点的个数:C(T)=∑N*H(T)+λ|T|;其中N为叶片样本个数,H为其熵。此式第一项表示所有叶节点熵的总和,第二项用来约束叶结点的个数,最小化此函数可以使得决策树在准确率与复杂度之间取得平衡。也就是说,在每次分裂之前,只有在此分裂使得C(T)减小时才会执行。
7.2. 分类和回归树(CART)
C由于算法1.2都是基于随机变量的熵,不能很好衡量回归问题中的收益;CART的回归算法基于MSE损失函数作为优化目标;对于CART的回归树,在每次节点划分时不仅要找到最优特征,还需要找到最优划分阈值。每次划分时都需要选择使两个区域的误差平方和最小的特征和阈值s。
而其分类算法基于基尼不纯度,在每次划分时都选择使总基尼不纯度最小的特征和阈值进行划分。基尼不纯度相较于信息增益率时间效率加快许多。基尼不纯度定义为:1-∑p(k)^2;当分布p越随机,基尼不纯度越大;而p越确定,基尼不纯度越小;这一性质和p的熵一样。
使用C4.5和CART进行分类的核心代码:
from sklearn import tree
#C4.5基于信息增益率
c45 = tree.DecisionTreeClassifier(criterion='entropy',max_depth=6)
c45.fit(X_train, y_train)
c45_train_pred = np.mean(c45.predict(X_train)==y_train)
c45_test_pred = np.mean(c45.predict(X_test)==y_test)
#CART基于基尼不纯度
cart = tree.DecisionTreeClassifier(criterion='gini',max_depth=6)
cart.fit(X_train, y_train)
cart_train_pred = np.mean(cart.predict(X_train)==y_train)
cart_test_pred = np.mean(cart.predict(X_test)==y_test)
7.3 总结
前剪枝:使用代价函数,最大深度等约束条件;
后剪枝:遍历节点判断分裂价值,从而删去部分叶节点。
| 特性 | ID3 | C4.5 | CART |
| 划分标准 | 信息增益 | 信息增益率 | 基尼指数/MSE |
| 处理类型 | 离散数据 | 离散和连续数据 | 离散和连续数据 |
| 生成结构 | 多叉树 | 多叉树 | 二叉树 |
| 主要应用 | 简单分类 | 复杂分类 | 分类+回归 |
| 算法优点 | 简单快捷 | 防止过拟合 | 生成简单结构 |
| 算法缺点 | 划分过精细 | 复杂度较高 | 复杂度稍高 |
8. 集成学习框架
集成学习(ensemble learning):将不同算法得到的模型按某些方式进行组合,取长补短从而得到更好的模型。
8.1. 自举聚合(Bagging)
由两部分组成;
1. 自举采样:为保证随机性尽可能降低不同子数据集之间的相关性【1】,允许重复的有放回采样,增加了模型的多样性;
2. 聚合:假设共进行了B次自举采样,分别在每个子数据集上独立的训练出模型,再用某种集成方法将这些模型组合起来(例如平均单个并行训练的模型的结果)
【1】:自举聚合模型在不同数据集上训练出的模型相关性较强时,降低方差的能力会被削弱。
测试评估:
包外(ODB)误差:对于每个样本x,选择训练集中不包含x的模型进行测试并得出误差;
聚合模型并不改变单一模型的期望偏差,但是可以缩小模型预测的方差。因此,bagging算法对于低偏差高方差模型(例如神经网络以及决策树等)的稳定性有较大提升。
缺点:bagging算法的底层基础模型要求是同一种类。
8.1.1. 随机森林
在决策树模型上使用bagging算法,得到的改进版本称为随机森林;
在随机森林中,树之间的相关性越高,集成模型的方差就会增加;所以为了更加降低模型相关性,在决策树每次分裂结点之前都从全部的M个特征中采样m个特征作为最优划分特征;一般来说取m=sqrtM.
随机森林算法相较于简单的bagging算法训练时间显著减少,且可以通过平均多个模型的结果以及随机选取数据以及特征有效防止过拟合。
核心代码:
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier
#bagging算法
bc = BaggingClassifier(n_estimators=100,oob_score=True,random_state=0)
bc.fit(X,y)
bc_score = bc.oob_score_
#随机森林算法
rfc = RandomForestClassifier(n_estimators=100,max_features='sqrt',oob_score=True,random_state=0) #使用m=sqrtM的随机森林
rfc.fit(X,y)
rfc_score = rfc.oob_score_
在随机森林中,有两个关键的随机选择步骤:
1. 训练数据随机:
每棵树的训练数据通过bagging中的自举算法进行有放回的随机选择数据点;
2. 特征选择随机:
在每个决策树的节点分裂时,随机选择一部分特征来决定最佳分裂点,避免树之间的高相关性。
8.2. 堆垛算法(Stacking)
堆垛算法的基本原理是:
训练多个可以是采用不同类型的的基学习器(base learner)来捕捉数据中的多模式和特征;再将基学习器的预测结果作为新的输入特征,通过元学习器(meta learner)进行二次学习,学习这些特征与真实标签之间的关系,从而优化最终预测。
**考虑到训练难度的问题,通常采用逻辑斯蒂回归作为元学习器。
其步骤如下:
1. 对训练数据进行k折交叉划分,并分配每个基学习器一组数据。对于每个基学习器,使用其他k-1个子集进行训练,并在该子集上进行预测。这样的训练保证了多样性和泛化能力。
2. 将基学习器在验证集上对样本的预测结果作为新的特征,将这些新的特征和原始的标签一起构建成为新的数据用于训练元学习器。元学习器学习到基学习器预测结果与真实标签之间的关系,提升最终预测效果。
3. 在进行最终评测时,对于新的数据,首先使用训练好的基学习器进行预测,生成新的特征数据;再将特征数据输入到元学习器中,得到最终的预测结果。
8.3. 提升算法(Boosting)
基本思路:通过逐步训练一系列弱学习器,每个模型都试图纠正前一个模型的错误。每一步的模型训练时都会根据前一步模型的错误率来调整样本的权重,使得后续模型更加关注那些被前面模型错分的样本。最终,所有弱学习器的预测结果进行加权组合,得到最终的预测结果。Boosting通过这种迭代的方式不断减少训练误差,从而提高模型的准确性。
即:假设已经在某一训练集上训练出f1,用f1预测结果的损失来调整f2中样本的权重,以此重复直到预设上限;最终得到n个模型f1,...,fn,称为弱学习器。这些弱学习器在数据集上各有侧重,将弱学习器进行加权求和,发挥他们不同的优势,最终得到强学习器。
8.3.1 适应提升(AdaBoost)
基本思路:初始化样本相同的权重;训练弱分类器后计算加权误差和分类器的权重,最后更新数据集中的样本权重,在迭代多次此步骤后得到强学习器。由数学推导可知,Adaboost与逻辑斯蒂回归在预测上可看作等价的。
在训练AdaBoost时,可以采用前向分布算法,向模型中不断添加弱学习器。假设模型的前m-1步的优化已经完成,得到了模型并将其固定。在第m步中,有F{m}=F{m-1}+α{m}*f{m},其中α是本轮优化等待学习的权重,f为新加入的弱学习器。通过最小化损失函数,可以求得最优的权重参数。
离散适应提升:弱分类器fm的输出只有1,-1两个值;
实适应提升:输出连续的实数;实际算法中将计算加权误差改为了估计样本类别的概率。
以桩(stump,深度为1的决策树)为基本单元的离散AdaBoost及实AdaBoost的准确性为例的核心代码:
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
#初始化stump
stump = DecisionTreeClassifier(max_depth=1, min_samples_leaf=1, random_state=0)
#离散AdaBoost,使用分布加性模型
dsc_adaboost = AdaBoostClassifier(estimator=stump, n_estimators=m, algorithm='SAMME', random_state=0)
dsc_adaboost.fit(X_train, y_train)
dsc_ada_score = dsc_adaboost.score(X_test, y_test)
#实AdaBoost
real_adaboost = AdaBoostClassifier(estimator=stump, n_estimators=m, algorithm='SAMME.R', random_state=0)
real_adaboost.fit(X_train, y_train)
real_ada_score = real_adaboost.score(X_test, y_test)
8.3.2 梯度提升(GDBoost)
仿照梯度下降算法,若将总函数看成损失函数的参数,那么新添加的弱学习器fm应当沿着总损失函数在F(m-1)处的梯度方向,其中F(m-1)为到第m-1步位置的弱学习器之和;这一方法采用了梯度作为优化目标:每次都最小化当前损失的梯度。注意超参数学习率不应当太大,其可以起到防止过拟合的作用。
应用:与决策树相结合,可以得到梯度提升决策树(GBDT)算法;若在损失函数中添加与决策树复杂度有关的正则化约束【γT+λ|w|^2/2;其中T为叶节点个数,w为叶片上的预测值组成的向量;其余字母为约束强度。】从而防止单个若学习器发生过拟合现象,称为梯度提升决策树(XGBoost)算法;这种算法得出的决策树结构更优秀:依靠此正则化约束可以求出预测向量w的最优解,从而得出损失函数的最小值。在每次分裂节点前,只有分裂后的最小损失函数变低时才会执行分裂操作。
XGBoost回归为例的核心代码:
from xgboost import XGBRegressor
xgbr = XGBRegressor(
n_estimators=100, #弱分类器数目
max_depth=1, #决策树最大深度
learning_rate=0.5, #学习率
reg_lambda=0.1, #L2正则化约束
subsample=0.5, #采样特征比例
random_state=0
)
XGB = xgbr.fit(X_train, y_train)
XGB_score = XGB.score(X_test,y_test) #R2分数(决定系数)
总的来说,适应提升算法中,每个弱学习器根据前一轮的错误率计算并调整不同学习器的权重,而梯度提升决策树通过用梯度下降的方法优化损失函数,组合多个弱分类器。 一般来说,梯度提升决策树的抗噪能力较强,过拟合风险较低,但是调参复杂度较大,训练时间更长。
8.4 总结
自举聚合和集成学习其利用模型之间取长补短的思想进行提升,各个模型互不干扰,可以并行训练;而提升框架希望模型组成序列依次优化,让后一个模型关注当前模型的缺陷和误差,需要串行训练。
| 特性 | Bagging | Stacking | Boosting |
| 基本概念 | 先有放回抽样单独训练基学习器,最后对结果进行平均 | 将多个基学习器通过元学习器组合成新的学习器 | 逐步训练多个基学习器使其关注前一个学习器的错误 |
| 样本权重 | 均等 | 均等 | 在迭代中根据正确率调整 |
| 基学习器 | 相同(如决策树) | 允许不同 | 相同(如决策树桩) |
| 训练过程 | 并行训练 | 基学习器并行训练,总体串行训练 | 串行训练 |
| 结果组合 | 平均基学习器的结果 | 基学习器的结果输入元学习器中 | 加权结合 |
| 最终目标 | 平均多个模型结果从而减少方差 | 同时考虑减少 | 关注难分类的样本从而减少偏差 |
9. 概率图模型
无监督学习中的数据分布建模问题;在概率图中一般会引入隐变量,用来表示观测不到的变量;
9.1 贝叶斯网络
由依赖关系构成的概率图是有向图,称为贝叶斯网络(Bayesian network);贝叶斯网络以贝叶斯推断为基础,由先验分布推导出后验分布;(有向边清晰的表明了先验和后验的关系)
贝叶斯网络的基本结构是三个变量的贝叶斯网络:
a) 尾对尾:在给定父节点时子节点条件独立
b) 头对尾:在给定中间节点时令两个节点条件独立
c) 头对头:在不给定子节点时两父节点天然独立
优化目标:希望让后验概率分布最大化,称为最大后验估计(MAP);
**MAP与MLE:两者的目标都旨在估计模型参数。对于先验知识,MLE不考虑先验分布,仅依赖于观测数据,希望最大化似然函数L(θ)=p(X|θ);而MAP则考虑了先验分布,将先验知识和观测数据结合,最大化后验分布p(θ|X)=p(X|θ)p(θ);通过后验分布还可看做引入了正则化,在样本较少时减少过拟合风险。
9.1.1 朴素贝叶斯
朴素贝叶斯是最简单的应用;其只需统计各个变量的先验分布(类别y的先验概率p(y)和各个特征在y条件下的概率p(x|y)),再由贝叶斯公式反推出参数的后验;
例如,可以用朴素贝叶斯完成文本分类,只需要统计先验概率:不同主题文章出现的频率(p(y)),以及主题为y的文章中单词x出现的频率(p(x|y))即可,最后统计一篇文章的单词向量和来进行归类。
过程如下:
首先需要将文本数据转化为特征向量:
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
X = news.data
y = news.target
#将文本数据转换为特征向量
vectorizer = TfidfVectorizer()
X_vec = vectorizer.fit_transform(X)
X_train,X_test,y_train,y_test = train_test_split(X_vec,y,test_size=0.2,random_state=0)
创建朴素贝叶斯模型完成离散特征多分类任务:
from sklearn.naive_bayes import MultinomialNB
mnb = MultinomialNB()
mnb.fit(X_train, y_train)
acc = mnb.score(X_test, y_test)
9.2 马尔可夫网络
将贝叶斯网络中的边改成无向边,即能得到马尔可夫网络。它用于描述几个变量之间是如何相互依赖的。
优化目标:所有极大团的能量之和
应用:图像去噪任务
9.3 期望最大化算法(EM)
在某些概率分布中(如高斯联合分布GMM),参数难以解析的计算,因此可以采用期望最大化算法:
1) E步骤:固定参数,计算隐变量的期望值;
2) M步骤:固定隐变量,最大化参数的对数似然,从而更新模型参数。
这样交替优化的方式又被称为坐标上升,例如k均值聚类与SVM的SMO算法都是EM/坐标上升算法的一种应用。
9.4 隐马尔可夫模型(HMM)
HMM用于描述具有隐含状态的马尔可夫过程,用于处理序列中含有隐含状态输出的时间序列数据。HMM可用于解决时间序列数据中的标注问题,其中观测数据是一致的,而隐藏状态是未知的。
HMM是生成模型,表示联合概率分布P(X,Y),其中X是观测序列,Y是隐藏状态序列。其进行独立假设,假设当前状态只依赖于前一个状态,观测值只依赖于当前的隐藏状态。
在训练方法上,其使用B-W算法(EM算法的一种)进行参数估计。由于基于极大似然估计,容易陷入局部最优。
然而,由于生成式模型的独立性假设,HMM适合简单的序列标注任务,例如词性标注,建模音素序列等。
9.5 条件随机场(CRF)
CRF是一种无向概率图模型,用于序列标注问题。它通过建模给定输入序列的条件下标签序列的条件概率进行标注。CRF解决了HMM在独立性假设上的局限性,直接建模输入序列与标签序列之间的条件概率。
CRF是判别模型,直接建模了条件概率分布P(Y|X),其中X是观测序列,Y是状态序列。其不要求独立假设,可以捕捉更复杂的依赖关系。
在训练方法上,其实用梯度下降法进行参数优化,比HMM表现更佳。CRF适用于需要捕捉复杂特征或长距离依赖的序列任务,例如命名实体识别NER和语义角色标注等。
然而,CRF的计算复杂度较高,训练过程相对复杂。
10. 双线性模型
双线性模型的含义为模型中包含双线性因子,该特性赋予一些非线性拟合数据的能力。双线性模型意为二元函数固定一个自变量时,另一个自变量与函数为线性关系。注意这样的函数不是广义线性函数。
10.1 矩阵分解(MF)
矩阵分解算法时推荐系统中评分预测的常用模型;其任务为根据用户对商品已有的评分来预测用户对其他商品的评分。具体来说,任务的输入是一个用户对于电影的评分矩阵R;然而由于用户只会对有限的一部分电影做出评分,因此R是极为稀疏的。因此,需要从R有限的元素中推测出用户的偏好P和特征Q。
MF算法的基本思想是假设用户i对电影j的评分 r[ij]是用户i的偏好向量与电影j的特征向量的内积,即 r[ij] = p[i] * q[j];因此可以将用户对物品的评分矩阵R分解为用户偏好矩阵P和物品特征矩阵Q的乘积:R = P @ Q^T;其中,P和Q的每一行/列都分别代表一个用户/物品的潜在特征向量。
MF算法的损失函数为还原结果和R中已知部分的差距作为损失函数;最后p和q中的特征参数可以由梯度更新得来。由于MF是双线性模型,p和q的梯度都是互相包含双方的。
最后,使用训练好的P和Q就能够还原出用户对电影的所有评分了。
10.2 因子分解机(FM)
FM也是推荐系统中用户行为预估的一个常用模型;MF的目标是从交互的结果中计算出用户和物品的特征,而FM的目标则是希望通过物品的特征和某个用户对于物品的点击率预测该用户点积其他物品的概率,即点击率(CTR)。
由于点击是一个二分类问题,CTR预估可以采用线性回归来解决;为了进一步表示出输入数据内部各个特征之间也有可能存在的关联,将双线性部分也考虑进来,写成向量形式为:
y_pred(x) = θ[0] + θ^T@x + 1/2 * x^T @ W @ x ;其中θ0是常数项,x是特征矩阵,W是权重矩阵。
由于物品特征是一个高维的独热向量,稀疏程度很高。这样在求梯度时就有很大概率得到0的结果,无法对参数进行更新。因此引入FM算法:权重矩阵W总是可以使用近似分解 W≈V@V^T 来代替。此时求得梯度的结果就不再会被稀疏矩阵影响到了。如果要做分类任务,只需要加入softmax函数即可。
四. 深度学习基本算法
1. 基础神经网络
1.1 人工神经网络(ANN)
神经元互相连接,构成有向图;神经元将前面所有神经元发送的信号通过连接权重加权求和(线性层),得到内部总信号;再通过一个预设的阈值来控制输出,模拟激励信号或抑制信号;
缺点:参数需要人为指定。
只使用了线性层的线性回归代码:
from torch.nn import nn
#定义模型
net = nn.Sequential(nn.Linear(2,1)) #假设有两个特征
loss = nn.MSELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.03)
#训练
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data:
l = loss(net(X), y) #正向传播的损失
optimizer.zero_grad() #清空梯度
l.backward() #梯度反向传播
optimizer.step() #更新模型参数
#得到训练结果
w = net[0].weight.data
b = net[0].bias.data
1.2 感知机
相较于ANN,在加入权重求和后引入了偏置项b,并且还通过激活函数(例如阶跃函数)来得到最终的输出。
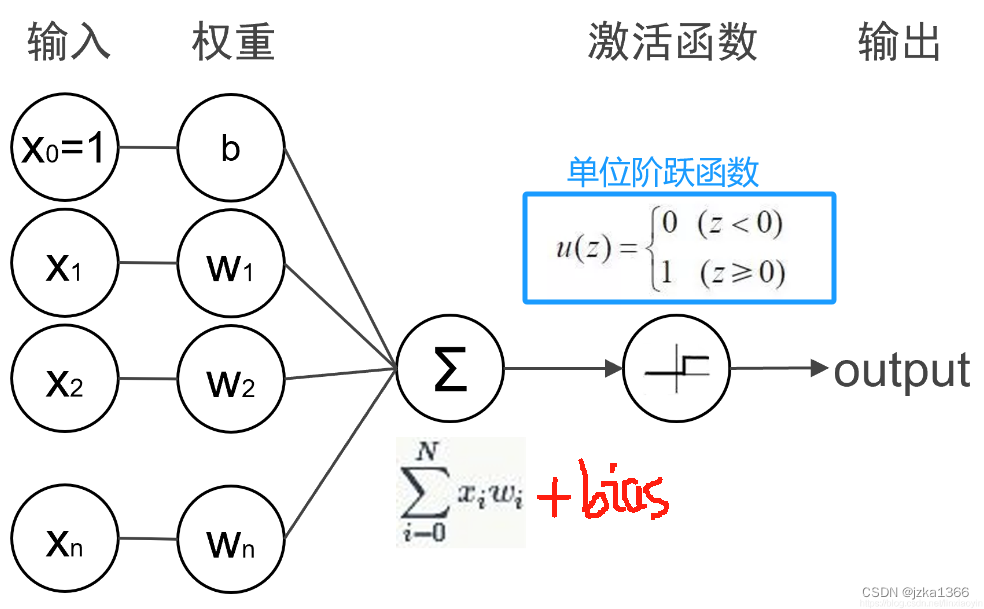
应用:二分类问题
优点:感知机最重要的进步在于它的参数可以自动调整。对于样本,感知机收到的反馈为 Δy=y_pred-y,其参数根据反馈进行更新:w<--w-η*Δy*x, b<--b-ηΔy.
缺点:只能处理线性可分的问题
1.2.1 二分类
以二分类为例的核心代码:
from sklearn.metrics import accuracy_score
import torch
import torch.nn as nn
import torch.optim as optim
class Perceptron(nn.Module): #感知机模型
def __init__(self, input_dim): #接受参数为输入特征的数量
super(Perceptron, self).__init__() #调用父类
self.linear = nn.Linear(input_dim, 1) #线性层(加权求和并加偏置)
def forward(self, x): #前向传播
return torch.sigmoid(self.linear(x)) #通过sigmoid激活函数
input_dim = X_train.shape[1] #数据集特征数量
model = Perceptron(input_dim)
criterion = nn.BCELoss() #二分类任务使用二元交叉熵损失
optimizer = optim.SGD(model.parameters(),lr=0.01) #随机梯度下降
num_epochs = 100
for epoch in range(num_epochs):
outputs = model(X_train) #前向传播
loss = criterion(outputs, y_train) #计算损失
optimizer.zero_grad() #清零梯度,防止累加前几次的梯度
loss.backward() #反向传播
optimizer.step() #参数更新
if(epoch+1)%10==0:
print(f'Epoch[{epoch+1}/{num_epochs}],Loss: {loss.item():.4f}')
# 评估模型
model.eval()
with torch.no_grad():
train_preds = model(X_train).round()
train_accuracy = accuracy_score(y_train, train_preds)
test_preds = model(X_test).round()
test_accuracy = accuracy_score(y_test, test_preds)
print(f'Train Accuracy: {train_accuracy:.4f}')
print(f'Test Accuracy: {test_accuracy:.4f}')
1.2.2 图片多分类
以用Softmax进行对于Fashion MNIST数据集多分类回归的完整详细代码:
1. 首先导入库并读入数据集
import torch
import torch.nn as nn
import torch.optim as optim
import pandas as pd
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
train_data = pd.read_csv('/kaggle/input/fashionmnist/fashion-mnist_train.csv')
test_data = pd.read_csv('/kaggle/input/fashionmnist/fashion-mnist_test.csv')
train_data.head()
2. 进行数据预处理
# 提取特征和标签
X_train = train_data.iloc[:, 1:].values
y_train = train_data.iloc[:, 0].values
X_test = test_data.iloc[:, 1:].values
y_test = test_data.iloc[:, 0].values
# 转换为PyTorch张量
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.long)
# 归一化数据,确保像素都在0~1间
X_train /= 255.0
X_test /= 255.0
# 打包数据集
train_dataset = TensorDataset(X_train, y_train)
test_dataset = TensorDataset(X_test, y_test)
#拆分成小批次
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)
3. 定义并创建模型
#定义模型
class Softmax(nn.Module):
def __init__(self):
super(Softmax, self).__init__()
self.linear = nn.Linear(28*28, 10)
def forward(self, x):
return self.linear(x)
#创建模型
model = Softmax()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
4. 训练并测试模型
#训练模型
num_epochs = 4
train_losses = []
test_losses = []
train_accuracies = []
test_accuracies = []
for epoch in range(num_epochs):
model.train()
train_loss = 0.0
correct = 0
total = 0
for images, labels in train_loader:
images = images.view(-1,28*28) #展平图像
outputs = model(images) #前向传播
loss = criterion(outputs, labels) #计算损失
optimizer.zero_grad() #清空梯度
loss.backward() #反向传播
optimizer.step() #优化参数
train_loss += loss.item() * images.size(0) #总损失=平均损失*总样本数
_, predicted = torch.max(outputs.data, 1) #最大值和其索引(最大的概率即对应预测类别)
total += labels.size(0) #样本数量
correct += (predicted == labels).sum().item() #预测正确了的样本数
train_loss /= len(train_loader.dataset) #数据集的平均损失
train_accuracy = 100 * correct / total
train_losses.append(train_loss)
train_accuracies.append(train_accuracy)
# 测试模型
model.eval()
test_loss = 0.0
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
images = images.view(-1, 28*28) #完全相同的操作
outputs = model(images)
loss = criterion(outputs, labels)
test_loss += loss.item() * images.size(0)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_loss /= len(test_loader.dataset)
test_accuracy = 100 * correct / total
test_losses.append(test_loss)
test_accuracies.append(test_accuracy)
print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {train_loss:.4f}, Train Accuracy: {train_accuracy:.2f}%, Test Loss: {test_loss:.4f}, Test Accuracy: {test_accuracy:.2f}%')
5. 模型可视化
# 绘制结果
epochs = range(1, num_epochs + 1)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(epochs, train_losses, 'bo-', label='Train Loss', markersize=4)
plt.plot(epochs, test_losses, 'ro-', label='Test Loss', markersize=4)
plt.title('Training and Testing Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(epochs, train_accuracies, 'bo-', label='Train Accuracy', markersize=4)
plt.plot(epochs, test_accuracies, 'ro-', label='Test Accuracy', markersize=4)
plt.title('Training and Testing Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.tight_layout()
plt.show()
1.3 多层感知机(MLP)
为了突破只能解决线性问题的困境,可以在感知机的基础上增加网络层数;将神经元分为不同的层,每一层至与前后相邻层的神经元连接。这样,可以将神经网络分为输入层,隐含层与输出层;
像这样将多个单层感知机按前馈结构组合起来,就形成了多层感知机MLP。每一层中,激活函数都是非线性的。考虑到对称性,一般让所有隐含层的激活函数相同;大多数情况下,线性整流单元ReLU(x)=max(x,0)(ReLU函数)作为隐含层的激活函数。而输出层的激活函数与任务对输出的要求直接相关。
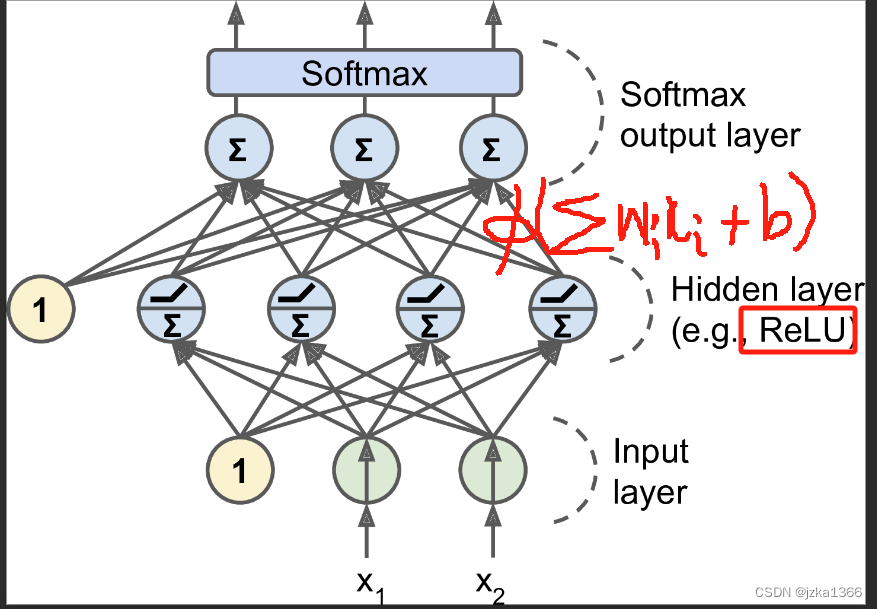
最简单的MLP实现:
import torch.nn as nn
net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
net(X)
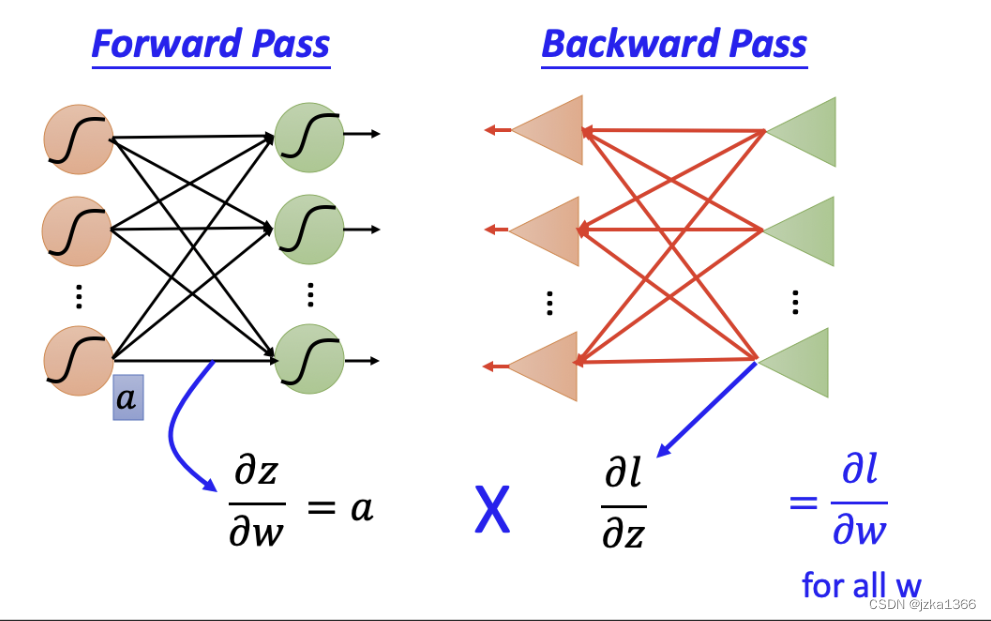
而为了调整MLP的参数,每一层的梯度由两部分组成,一部分是当前激活函数计算出的梯度,另一部分是后一层回传的梯度;这样的算法被称为反向传播(BP)算法;
具体来说:
假设模型希望最小化的目标(即损失函数)为L,每一层的权重为W,每一层的输出为 z=Φ(∑wx+b),则由链式法则有 ∂L/∂W = ∂L/∂z * ∂z/∂W;其中,∂z/∂W为每一层输出后可经计算算得得梯度,为当前前向传播得梯度;而 ∂L/∂z 则是依靠模型全部计算结束后从后往前传递的回传梯度来计算。
使用这样的方法将每一层的梯度写成正向梯度与回传梯度乘积计算的算法即被称为反向传播(backpropagation)BP算法。最后,假设学习率为 η,那么就可更新参数为 W<--W-η*∂L/∂W。与权重更新类似的,偏置b也可以经过相同的反向传播来更新其参数。
当数据量较小或模型复杂时,容易发生过拟合;可以使用暂退法(Dropout)来进行缓解;它是一种正则化技术,通过在训练过程中随机丢弃一部分神经元来减少神经元之间的依赖性,从而提高模型的泛化能力。
以丢弃概率为0.5为例的模型构建代码:
import torch.nn as nn
#以图片分类为例
Class MLP=(nn.Module):
def __init__(self)):
super(MLP, self).__init__()
self.hidden1 = nn.Linear(28*28,256) #从28*28的像素输入到256个神经元的隐藏层
self.hidden2 = nn.Linear(256, 128) #从256到128的隐藏层
self.output = nn.Linear(128, 10) #最后输出为10个特征
self.relu = nn.ReLU() #用relu作为隐藏层的激活函数
self.dropout = nn.Dropout(p=0.5) #用0.5的概率丢弃神经元
def forward(self, x):
#第一层:线性->激活->丢弃
x = self.relu(self.hidden1(x))
x = self.dropout(x)
#第二层
x = self.relu(self.hidden2(x))
x = self.dropout(x)
#全连接层输出
x = self.output(x)
return x
1.3.1 图片多分类
与1.2.2相同,我们使用MLP来分类fashion MNIST数据集;其中,第1.2.4.5步与1.2.2中的代码相同,只展示第三部分定义并创建模型的MLP版代码:
#定义模型
class MLP(nn.Module):
def __init__(self):
super(MLP, self).__init__()
self.hidden1 = nn.Linear(28*28, 256)
self.hidden2 = nn.Linear(256, 128)
self.output = nn.Linear(128, 10)
self.relu = nn.ReLU()
def forward(self, x):
x = self.relu(self.hidden1(x))
x = self.relu(self.hidden2(x))
x = self.output(x)
return x
#创建模型
model = MLP()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
除了定义类,在pytorch中还可以使用nn.sequential来简介实现:
import torch
import torch.nn as nn
import torch.optim as optim
model = nn.Sequential(
nn.Linear(28*28, 256)
nn.ReLU()
nn.Dropout(0.2)
nn.Linear(256, 128)
nn.ReLU()
nn.Dropout(0.5)
nn.Linear(128, 10)
)
loss = nn.CrossEntropyLoss()
opt = optim.Adam(model.parameters(), lr=0.1)
1.3.2 二分类异或数据集
import torch
import torch.nn as nn
import torch.optim as optim
#构建模型
class MLP(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(MLP, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
#设置参数
input_dim = 2
hidden_dim = 10
output_dim = 2
model = MLP(input_dim, hidden_dim, output_dim)
#定义损失和优化
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(),lr=0.01)
#训练模型
num_epochs = 100
train_losses=[]
test_losses=[]
test_acc_lst = []
for epoch in range(num_epochs):
#向前传播
outputs = model(X_train)
loss = criterion(outputs, y_train)
#反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
#记录损失
train_losses.append(loss.item())
#评估模型
with torch.no_grad():
test_outputs = model(X_test)
test_loss = criterion(test_outputs, y_test)
test_losses.append(test_loss.item())
_, predicted = torch.max(test_outputs, 1)
test_acc = (predicted == y_test).float().mean().item()
test_acc_lst.append(test_acc)
#打印进度
if(epoch+1)%10==0:
print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {loss.item():.4f}, Test Loss: {test_loss.item():.4f}, Test Accuracy: {test_acc:.4f}')
1.3.3 回归任务
1. 导入所需要的库&预处理数据
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
#导入数据,假设有两个特征进行预测
data = pd.read_csv('prediction_file_path.csv')
X = data[['feature1', 'feature2']].values
y = data['target'].values
# 数据标准化
scaler = StandardScaler()
X = scaler.fit_transform(X)
#转化为张量
X = torch.tensor(X, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.float32).view(-1, 1)
# 训练集和测试集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
2. 定义模型,损失函数以及优化器
#假设模型使用了两层隐含层
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(2, 64)
self.fc2 = nn.Linear(64, 32)
self.fc3 = nn.Linear(32, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = self.fc3(x)
return x
model = Net()
# 损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
3. 训练和验证
num_epochs = 100
train_losses = []
test_losses = []
r2_scores = []
for epoch in range(num_epochs):
# 训练阶段
model.train()
optimizer.zero_grad() #清空梯度
outputs = model(X_train) #前向传播
loss = criterion(outputs, y_train) #计算损失
loss.backward() #反向传播
optimizer.step() #优化参数
# 验证阶段
model.eval()
with torch.no_grad():
test_outputs = model(X_test)
test_loss = criterion(test_outputs, y_test)
r2 = r2_score(y_test.numpy(), test_outputs.numpy()) #决定系数
train_losses.append(loss.item())
test_losses.append(test_loss.item())
r2_scores.append(r2)
if (epoch+1) % 10 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {loss.item():.4f}, Test Loss: {test_loss.item():.4f}, R2 Score: {r2:.4f}')
4. 可视化结果
# 损失曲线
plt.figure(figsize=(10,5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss during training')
plt.legend()
# R2 Score曲线
plt.subplot(1, 2, 2)
plt.plot(r2_scores, label='R2 Score')
plt.xlabel('Epoch')
plt.ylabel('R2 Score')
plt.title('R2 Score during training')
plt.legend()
plt.tight_layout()
plt.show()
# 可视化预测结果
model.eval()
with torch.no_grad():
predicted = model(X_test).numpy()
y_test_actual = y_test.numpy()
# 反标准化
y_test_actual = scaler.inverse_transform(y_test_actual)
predicted = scaler.inverse_transform(predicted)
plt.figure(figsize=(6,6))
plt.scatter(y_test_actual, predicted, alpha=0.7)
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual vs Predicted Prices')
plt.plot([y_test_actual.min(), y_test_actual.max()], [y_test_actual.min(), y_test_actual.max()], 'k--', lw=2)
plt.show()
2. 卷积神经网络(CNN)
CNN非常擅长处理具有网格结构的数据,例如图像;其通过卷积运算来提取输入数据的特征。
相较于MLP神经元层之间的线性连接结构,卷积神经网络使用了卷积运算作为层与层之间的连接;在CNN中进行卷积运算的层称为卷积层;其由于非线性的连接而更适合提取高维特征的运算和数据结构。
卷积的本质是某种特殊的加权平均;例如在面对图像输入任务时,可将图像g看作由像素点组成的信号,不同位置的权重f代表了图像上不同像素的重要程度;在训练中,可将权重f设置为参数,通过GDBP算法进行训练并自动调整其值。
层中的权重f又称为卷积核,其尺寸称为感受野。较小的卷积核可以提取局部特征,而较大的卷积核可以发现整体特征。因此,在CNN中常常会使用多种尺寸的卷积核来提取不同尺度的有效信息,卷积核的数量也被称为通道(channel)。
此外,若希望输出图像能保持与输入图像相同的尺寸,可以对输入图像进行填充(padding)操作;常用方式有全零填充,常数填充和边界扩展填充。
而图像一般会有大量相同像素造成大量冗余信息,因此用一个像素来代表一片区域内的所有像素,从而降低整体的复杂度。这样的下采样操作成为池化(pooling),常用方式为平均池化和最大池化。注意池化操作运算的窗口滑动时不会重复。
卷积操作公式:a'=(a+2p-f)//s+1,其中a为边长,p为填充,s为步长,f为核大小。池化操作公式:a'=a//s。一般来说,对于池化操作,选用stride与kernel size为相等的整数;而对于卷积操作,一般选用stride=1,那么公式就可简化为a'=a+2p-f+1;若希望使卷积的结果不改变图像的大小,应当有f=2p+1;这就是为什么通常选用大小为奇数的卷积核。
代码参数介绍:
假设我们需要实现一个简易的CNN,由一个卷积,一个激活relu函数,一个最大池化,和一个全连接层构成;
还假设我们的输入是一个28*28像素的图片(比如MNIST数据集)
model = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=2),
nn.ReLU()
nn.MaxPool2d(kernel_size=2, stride=2)
nn.Flatten()
nn.Linear(14*14*6, 84)
nn.Linear(84, 10)
)
第一行代表了卷积操作;1是初始通道数(灰度图片的像素为1;若为彩色RGB图像通道数则是3),此时图像的大小为28*28*1(高*宽*通道数 H*W*C);
而6则是一个认为指定的来提取特征的参数,代表了第一个卷积层卷积核的数量为6;(卷积层通常会增加通道数来提取更多的特征)
后面的三个参数依次是卷积核的大小 ,步幅(一般设定为1),和填充数(用来保留边缘像素或控制输出的尺寸不变);这三个参数则控制了输出图像的边长大小;对于高和宽,公式为:output_size = [(input_size - kernel_size + 2*padding) // stride ] + 1;
所以在第一层卷积层过后,高和宽变为 (28-5+2*2)/1 + 1 = 28;故其尺寸变为 28*28*6。
第二行是用ReLU实现的激活函数,不改变大小;
第三行实现了最大池化,其中池化的核大小与步幅均为2(一般来说池化层的核和步幅大小相等);池化层不改变通道,但是由 output_size = input_size // stride 这一公式来计算长与高的改变,在这里则是 28//2=14,最后输出 14*14*6 的大小进入全连接层;
第四行是一个展平函数,将多为张量转换为一维张量,以便输入进全连接层中;
第五行是用一个线性层实现了全连接层,将14*6*6的大小输出为84再传入输出层中;最后输出层将其输出10个特征分别的概率即可。
CNN减少过拟合的方法:
1. 暂退法(Dropout):每次前向传播时,随机把输入中一定比例的神经元暂时遮盖住使他们不产生梯度回传,降低模型复杂度;
2. 数据增强:随机翻转,改变颜色,以及添加噪声,防止模型只学习到纹理和颜色而非图像轮廓。
2.1 图像分类--LeNet
LeNet-5结构式CNN最早的实用结构之一,应用在手写数字识别上;
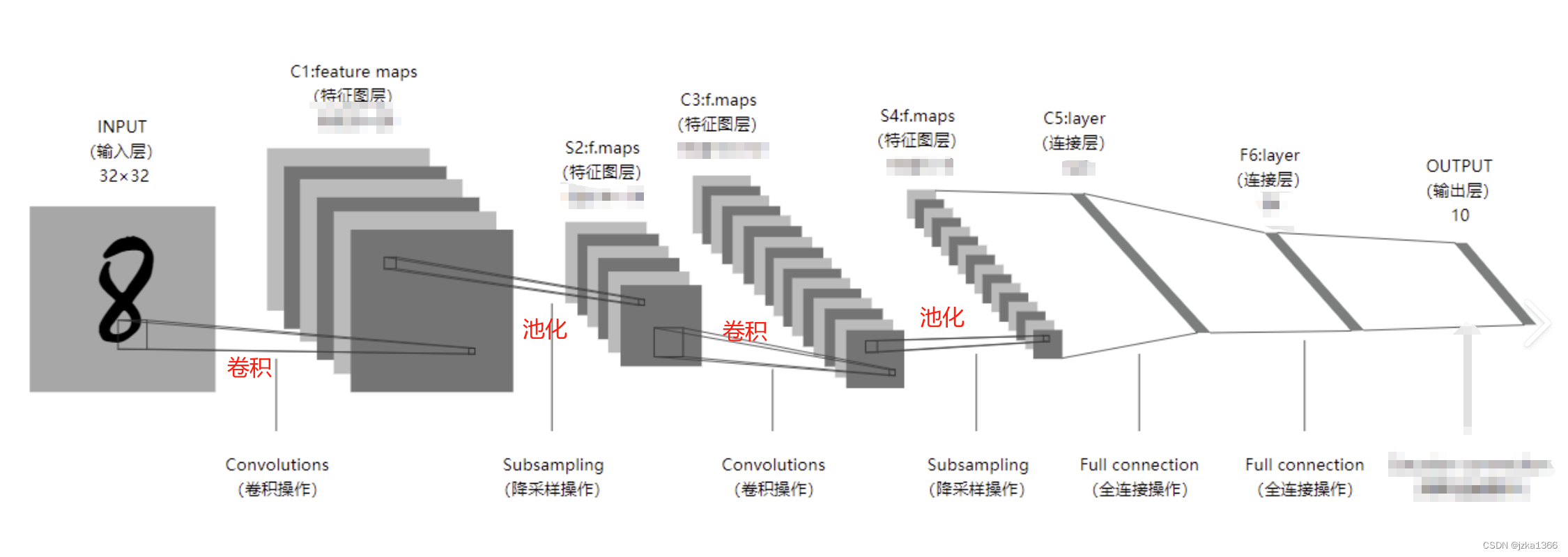
除去输入输出层,LeNet由两个卷积+池化的组合再连接两个全连接层构成(类似于上文的那段代码实现的扩展)
详细代码实现:
1. 首先,导入库和数据集:
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.utils.data import DataLoader, Dataset
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
import os
from tqdm import tqdm
#输入数据
train_data = pd.read_csv('/kaggle/input/mnist-in-csv/mnist_train.csv')
test_data = pd.read_csv('/kaggle/input/mnist-in-csv/mnist_test.csv')
2. 数据预处理
# 提取特征和标签
X_train = train_data.iloc[:, 1:].values.reshape(-1, 28, 28)
y_train = train_data.iloc[:, 0].values
X_test = test_data.iloc[:, 1:].values.reshape(-1, 28, 28)
y_test = test_data.iloc[:, 0].values
# 转换为PyTorch张量
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.long)
# 归一化数据
X_train /= 255.0
X_test /= 255.0
# 插入通道维度
X_train = X_train.unsqueeze(1) # 插入通道维度,形状变为 [batch_size, 1, 28, 28]
X_test = X_test.unsqueeze(1)
# 创建DataLoader
train_dataset = TensorDataset(X_train, y_train)
test_dataset = TensorDataset(X_test, y_test)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)
3. 定义LeNet-5的具体结构:
model = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0), nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16*5*5, 120), nn.ReLU(),
nn.Linear(120, 84), nn.ReLU(),
nn.Linear(84, 10)
)
4. 进行训练:
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
# 记录损失和准确率
train_losses = []
test_losses = []
train_accuracies = []
test_accuracies = []
# 训练模型
num_epochs = 3
for epoch in range(num_epochs):
model.train()
train_loss = 0.0
correct = 0
total = 0
for images, labels in train_loader:
# 前向传播
outputs = model(images)
loss = criterion(outputs, labels)
# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 累积损失
train_loss += loss.item() * images.size(0)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
# 计算平均损失和准确率
train_loss /= len(train_loader.dataset)
train_accuracy = 100 * correct / total
train_losses.append(train_loss)
train_accuracies.append(train_accuracy)
# 测试模型
model.eval()
test_loss = 0.0
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
outputs = model(images)
loss = criterion(outputs, labels)
test_loss += loss.item() * images.size(0)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
test_loss /= len(test_loader.dataset)
test_accuracy = 100 * correct / total
test_losses.append(test_loss)
test_accuracies.append(test_accuracy)
print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {train_loss:.4f}, Train Accuracy: {train_accuracy:.2f}%, Test Loss: {test_loss:.4f}, Test Accuracy: {test_accuracy:.2f}%')
5. 可视化结果
# 绘制结果
epochs = range(1, num_epochs + 1)
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(epochs, train_losses, 'bo-', label='Train Loss', markersize=4)
plt.plot(epochs, test_losses, 'ro-', label='Test Loss', markersize=4)
plt.title('Training and Testing Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(epochs, train_accuracies, 'bo-', label='Train Accuracy', markersize=4)
plt.plot(epochs, test_accuracies, 'ro-', label='Test Accuracy', markersize=4)
plt.title('Training and Testing Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
2.2 图像分类--AlexNet
AlexNet最初被应用在ImageNet挑战赛上,数据集是一个224*224像素的单通道灰度图片集合;

核心代码:
alexnet = nn.Sequential(
nn.Conv2d(1, 96, kenel_size=11,stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
nn.Linear(6400, 4096),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 10)
)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
num_epochs = 10
for epoch in range(num_epochs):
model.train()
for images, labels in train_loader:
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
3. 循环神经网络(RNN)
循环神经网络主要用于具有序列特征的数据,让网络能够提取先前的信息与现在信息的关联;其通过递归连接在时间步之间传递信息,能够记忆之前时间步的状态。
基本原理:
将多个MLP沿着序列不断扩展下去,中间的每个MLP都将前一时刻的中间变量与当前的输入组合得到新的中间变量,再继续后续处理;具体的组合规则如下(以NLP自回归为例):
首先将输入的序列中当前时间步t的数据(词或字母)取出,由word2vec词嵌入改写为低维的稠密向量表示,假设为e[t];隐含层 h[t]=σ(W1*h[t-1]+W2*e[t]+b1) 将前一步的隐状态h[t-1]与当前步的输入由固定的参数W1与W2进行加权求和,加入偏置b1并用sigmoid函数完成非线性变化。最后的输出即为 y[t]=softmax(U*h[t]+b2),相当于将隐状态通过全连接层对其维度并用softmax函数转化为概率分布。
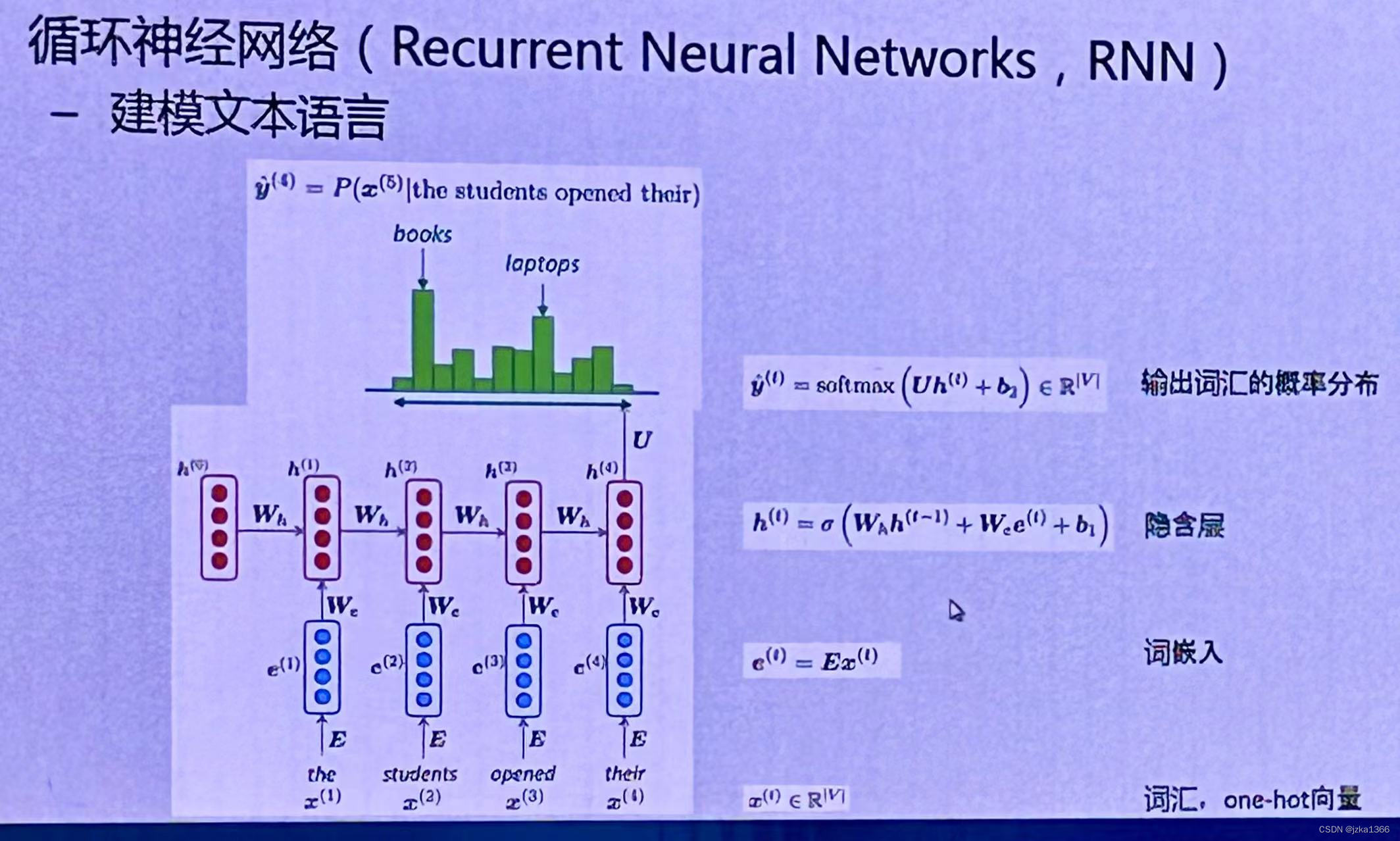
也就是说,每进行一组输入及预测,就保留他们的信息作为对于过去观测结果的总结,然后继续更新预测和总结;可以用公式 h(t)=g(h(t-1), x(t-1)) 表示,其中h为中间变量(对于过去的总结);这样的模型也被称为隐变量自回归模型(由于是对自身进行回归)。
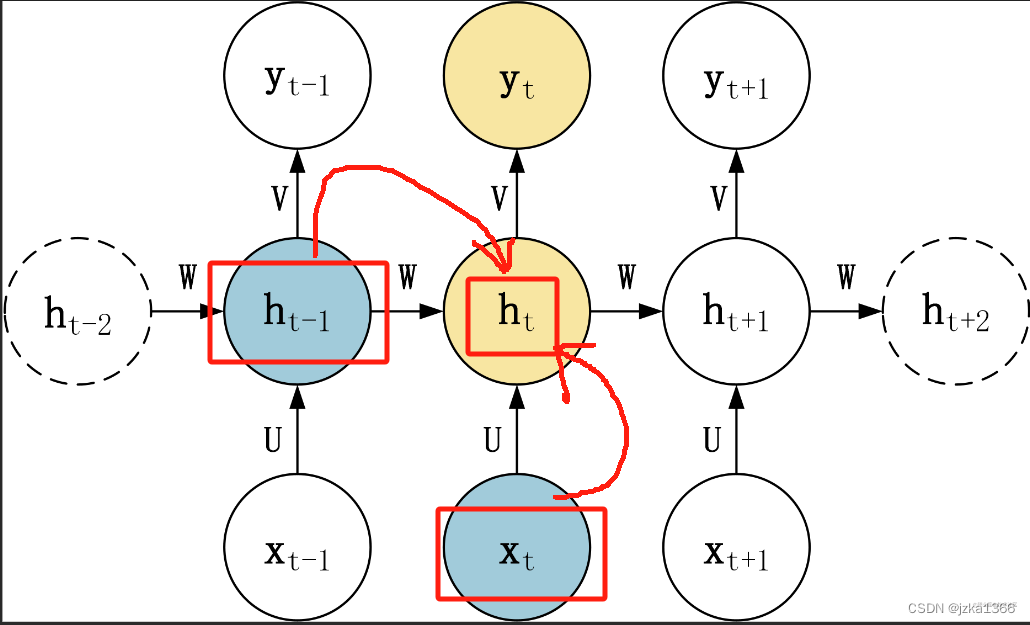
同时,又由于序列中每一个位置之间又存在对称性,每一个MLP前后的权重与中间组合的权重可以共用,不随序列位置变化,因此称为循环神经网络;
在时刻t若存在输出,则可以计算此时的损失函数,并用梯度回传的方法优化参数;
总结:CNN可以有效地处理空间信息,而RNN可以有效地处理序列信息;
在训练之前,需要定义输入序列的长度seq_len;在pytorch中,rnn的输出为中间变量,还需要拼接MLP来进行输出,并且要调整输出格式。核心代码如下:
class RNNModel(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNNModel, self).__init__()
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
h0 = torch.zeros(1, x.size(0), hidden_size).to(x.device)
out, _ = self.rnn(x, h0)
out = self.fc(out[:, -1, :])
return out
然而,随着反向传播步数的增加,RNN可能会出现梯度消失或梯度爆炸的现象,除了有类似梯度截断(又称梯度裁剪gradient clipping,即在训练时将梯度投影回给定半径的球来截断梯度)的方法,还可以使用长短期记忆网络(LSTM)进行优化;
3.1 门控循环单元(GRU)
GRU是一种简化了LSTM的模型;
为了调整相邻时刻两个中间变量(假设为h(t-1)与h(t))的关系,定义了两个门控单元:更新门和重置门;
具体来说,在由h(t-1)计算h(t)时,必须有选择的进行遗忘;同时,在时刻t由新的信息输入网络,需要在过去的信息h(t-1)与新的信息x(t)之间做到平衡。
第一步经过重置门,来对过去的信息h(t-1)做到选择性遗忘;当重置单元某维度接近0,网络就倾向于遗忘h(t-1)的相应维度,反之接近1则倾向于保留;这一步的结果称为候选隐状态;
第二步经过更新门,利用更新单元z(t),若其更接近0就保留更多旧信息,反之若其接近1则网络会让旧信息与新输入x(t)进行混合。
也就是说,重置门控制旧信息保留的比例,从而捕获序列中的短期依赖关系;更新门控制新信息输入的比例,从而捕获序列中的长期依赖关系。
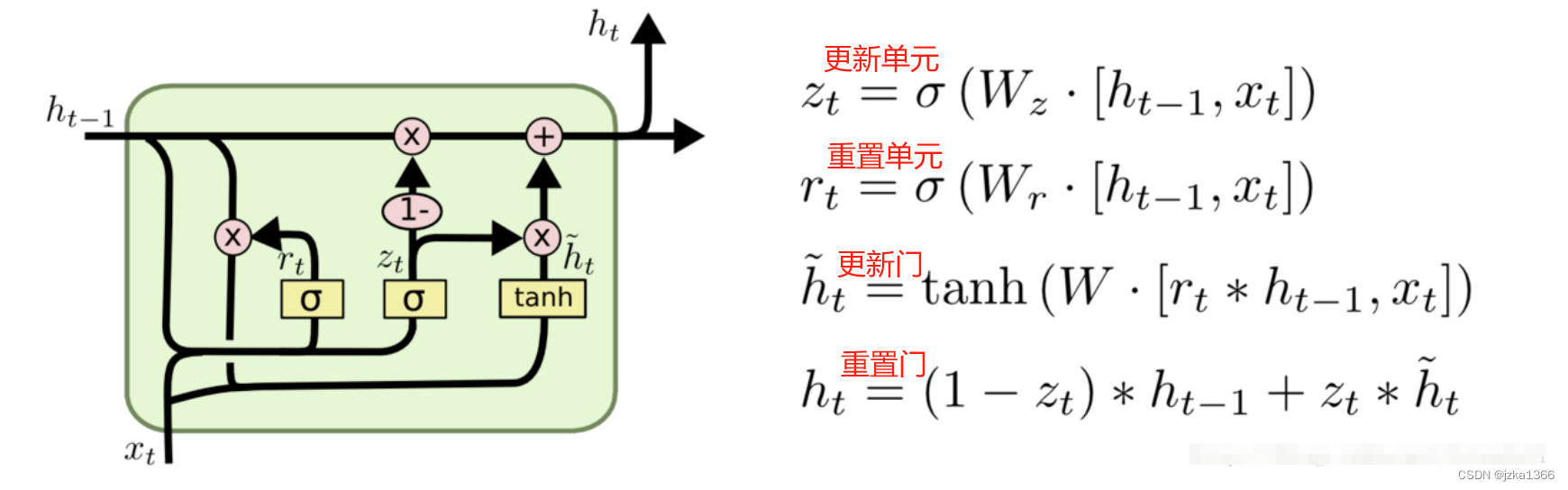
引入GRU后使得RNN可以自我调节梯度 。更新门允许隐藏状态直接赋值前一时间步的值,这使得信息可以长时间保留而不过多变形。这提供了一条无障碍的梯度传播路径。而门控机制的引入还使得网络在计算隐状态时,只需要对当前时间步和前一时间步的信息进行局部计算,降低了梯度爆炸的风险(因为梯度在传递过程中不会被反复放大)。
其核心代码与RNN基本相同(将RNN改为GRU即可):
class GRUModel(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(GRUModel, self).__init__()
self.gru = nn.GRU(input_size, hidden_size, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x):
h0 = torch.zeros(1, x.size(0), hidden_size).to(x.device)
out, _ = self.gru(x, h0)
out = self.fc(out[:, -1, :])
return out
总结:GRU与RNN最关键的区别在于GRU支持隐状态以及其加入了可学习的门控机制 。
**双向循环神经网络bidirectionalRNN添加了反向传递信息的隐藏层,使模型能从后往前提取信息。
3.2 长短期记忆网络(LSTM)
LSTM引入了记忆元,或可简称为单元(Cell);单元负责长期信息的存储,也可以看作是传递链条,贯穿LSTM的结构。
输出门决定从记忆单元中输出多少信息作为当前时间步的隐藏状态;
输入门决定当前时间步需要写入多少新信息到记忆单元中;
遗忘门用来决定当前时间步需要丢弃多少信息;
优点:梯度具有稳定性
与GRU的关系:GRU没有显式的记忆单元,隐状态直接承担了长期信息存储和短期状态更新的角色;此外,GRU合并了LSTM的输入门和遗忘门,形成了更新门。
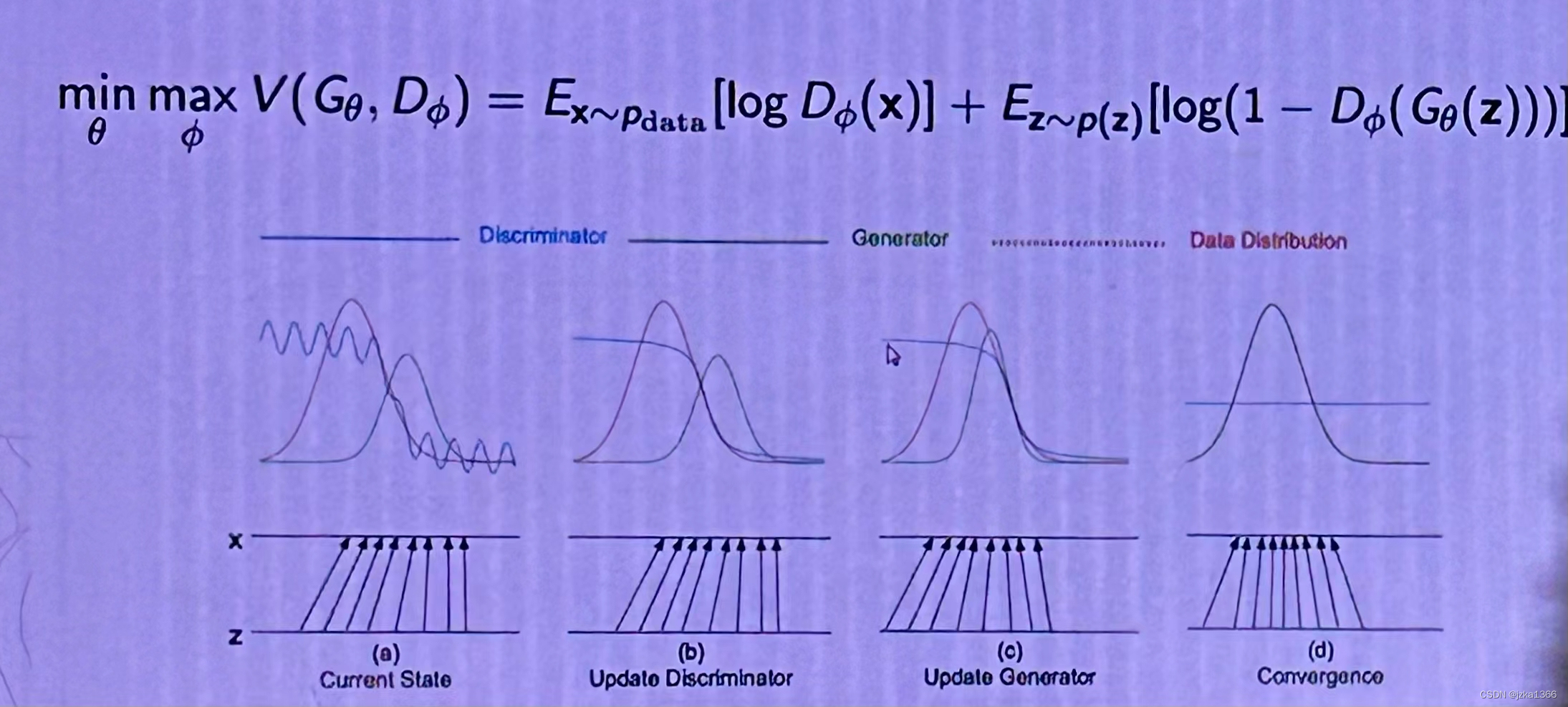
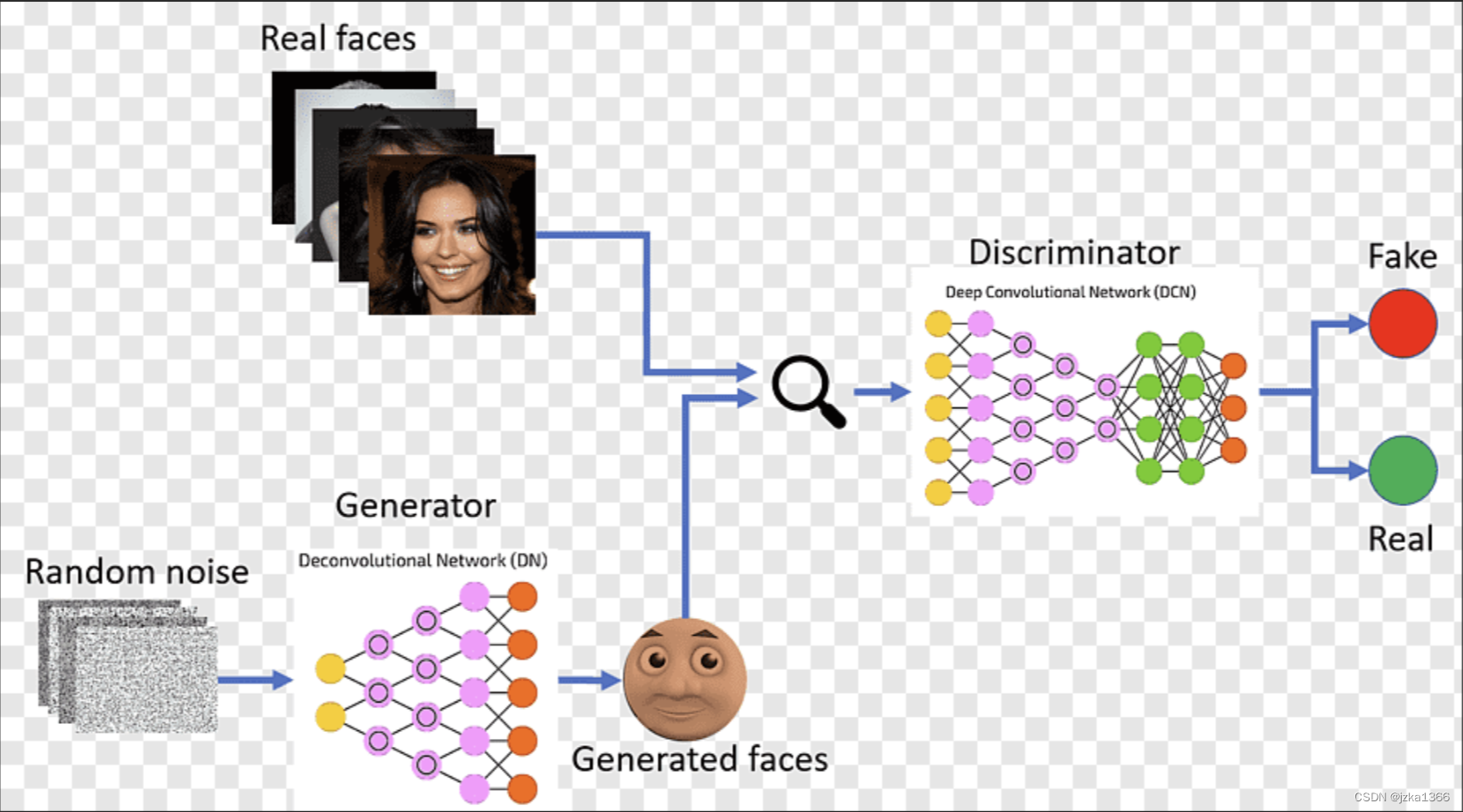
4. 生成式对抗网络(GAN)
生成对抗网络由两个核心组件组成:生成器(Generator)和判别器(Discriminator);这两个网络通过一种“对抗”的方式进行训练,最终生成逼真的数据。理论上的优化过程如下:
生成器(G):
任务:接受随机噪声作为输入,并生成尽可能逼真的数据样本;
目标:欺骗判别器,使判别器无法区分生成的数据和真实数据;
结构:使用反卷积网络(DN);反卷积网络能够实现通过上采样过程,将低维噪声映射到高维的数据空间。具体来说,反卷积网络可以被视为卷积网络的逆操作,通过转置卷积操作实现了从低维到高维的映射,使得生成器能够逆向操作,从噪声向量生成图像。
损失函数:生成的样本被错误分类为真实样本的负对数似然;
判别器(D):
任务:接受未知类别的输入样本作为输入,输出一个概率值表示真实数据的概率;
目标:尽可能区分出真实数据还是生成器生成的数据;
结构:使用深度卷积神经网络(DNN);判别器需要对输入的数据进行有效的特征提取,卷积神经网络可以提取出图像的局部特征以及全局结构信息。而使用深度架构(多层卷积和池化操作)可以学习到更复杂的特征表示。
损失函数:真实样本被错误分类和生成样本被错误分类的负对数似然的加权和。
训练过程:
首先初始化G和D的参数;重复以下步骤直到生成的数据足够逼真:
1. 训练判别器D:
从真实数据集随机采集样本,再从噪声分布中随机采样并让生成器生成假数据;给判别器训练后计算它的损失并更新判别器参数;
2. 训练生成器G:
从噪声分布中随机采样并让生成器生成假数据,再给判别器判断;之后计算出它的损失函数并更新生成器参数。
GAN的问题:训练不稳定或模式崩溃
GAN的应用:图像生成,修复,风格迁移,语音生成
5. 自编码器(AE)
自编码器是一个用神经网络无监督提取特征的算法,它将一个输入数据样本压缩成低维向量表示(编码器),然后基于低维特征向量恢复出接近于原始样本的输出(解码器);而直接使用神经网络学习编码解码,再用反向传播的方式自动更新参数的模型就成为自编码器(Auto Encoder)。一般来说,简单的MLP就能满足任务的要求;
**注意:编码与解码过程并不是对称的。
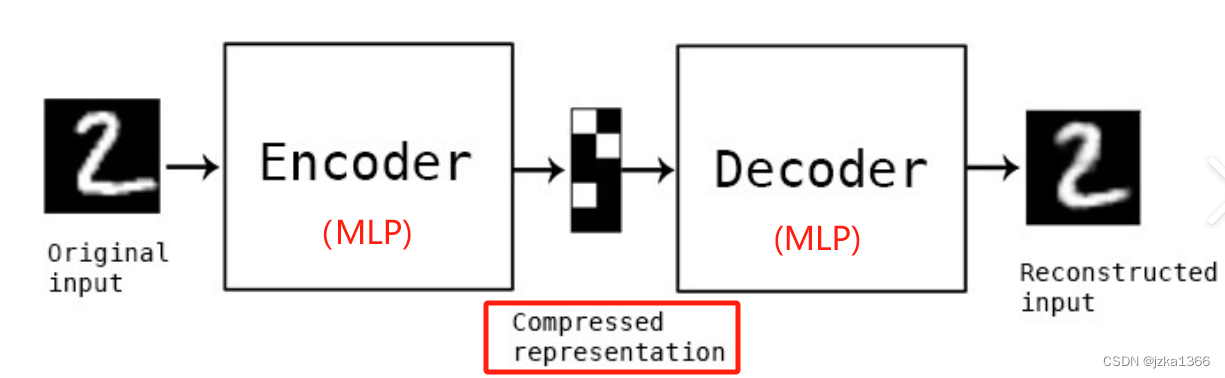
AE的应用包括数据压缩后重建,图像压缩,去噪,拟合数据分布,以及在cv和nlp中;还能够应用RNN实现AE,从而完成seq2seq序列到序列的机器翻译任务。
实例代码:
#多层感知机
class MLP(nn.Module):
def __init__(self, layer_sizes):
super().__init__()
self.layers = nn.ModuleList() #ModuleList用列表存储PyTorch模块
num_in = layer_sizes[0] #输入层的神经元数量
for num_out in layer_sizes[1:]:
#创建全连接层(在这里使用线性层)
self.layers.append(nn.Linear(num_in,num_out))
#创建逻辑斯蒂激活函数层
self.layers.append(nn.Sigmoid())
num_in = num_out
def forward(self, x):
#前向传播
for l in self.layers:
x = l(x) #遍历每一层进行传播
return x
五. 深度学习应用
1. 自然语言处理(NLP)
自然语言处理(NLP)任务类型包括文本分类、情感分析、命名实体识别、机器翻译、问答系统、语音识别、摘要生成和词性标注。
1.1 文本预处理
自然语言处理任务的第一步就是进行文本预处理(text preprocessing),以方便作为数值输入pytorch模型进行操作。
首先导入文件并将字母的大写转化为小写,统一文本格式:
import re
def clean_text(text):
text = re.sub(r'[^a-zA-Z\s]', '', text) # 去除非字母字符
text = text.lower() # 转换为小写
return text
cleaned_text = clean_text(text)
print(cleaned_text)
然后进行词元化(tokenization):
词元化,又称词法分析,是指将原始文本分割成模型可识别和建模的词元序列;序列中可以是单词,标点,数字等。
其主要步骤包括:
1. 文本预处理;2. 分词,将文本分割成独立的词汇单位;3. 标记化:将分割后的词汇单位标记为不同类型。
词法分析的方法:
1. 基于规则的分词:使用预定义的规则,例如词典,进行分词;适用于拼写规范的语言,例如英文;
2. 基于统计的分词:使用隐马尔可夫等模型分词,适用于不规范的语言,例如中文;
3. 基于机器学习:可以使用神经网络或条件随机场等学习分词规则;
词法分析的挑战:
1. 歧义性:词与词之间没有明显的边界会导致多种分词结果;
2. 多义性:一个词可能有多个意义;
3. 新词检测:语言不断进化,新的词汇不断出现。
示例代码如下,这里使用了nltk库:
from nltk.tokenize import word_tokenize
#分词
tokens = word_tokenize(cleaned_text)
print(tokens)
其次需要为出现的单词统计频率,来了解文本数据中出现的独特单词;返回的counter是一个字典,存储了每个被分词分出的单词以及这个单词所对应的出现频率;这一步统计得到的结果成为语料库(corpus)。
from collections import Counter
corpus = Counter(tokens)
print(corpus)
接下来需要建立一个词表(volcabulary),将拆分的词元映射到数字索引之上;频率高的单词通常会获得较小的索引值;输出的将会是一个字符串映射到索引的列表。
word_to_index = {word: idx for idx, (word, _) in enumerate(corpus.items())}
print(word_to_index)
最后的步骤是将文本转换为数字索引序列,以方便模型操作;
indexed_sequence = [word_to_index[word] for word in tokens]
print(indexed_sequence)
另外,其他的可选步骤还包括去除停用词和词干提取:
去除停用词的目的是去除常见但无意义的词,如the和is等,减少词汇量,提高泛化能力:
from nltk.corpus import stopwords
#英文停用词
stop_words = set(stopwords.words('english'))
#去除停用词
def remove_stopwords(tokens):
filtered_tokens = [word for word in tokens if word not in stop_words]
return filtered_tokens
filtered_tokens = remove_stopwords(tokens)
print(filtered_tokens)
下采样也可以实现类似的效果:当训练词嵌入模型后,可以对高频词进行下采样:每个单词会以一定的概率被丢弃,这个概率与单词站数据集的比例成正比。
要降低停用词的权重还可以使用TF-IDF模型:
特征提取的一种,计算词在文档中的出现频率(TF)与词再整个语料库中出现的逆频率(IDF);能够降低高频词(如停用词)的权重,提高重要但不常见的词的权重。
**逆频率IDF衡量了一个词在整个文档集合中的重要性;
此外,还有词干提取和词形还原(stemming and lemmatization):
词干提取是将单词去除词缀还原为其词根形式;而词形还原的目的是将单词还原为其字典中的基本形式,例如比较级转化为原型。
| 特性 | 词干提取 | 词形还原 |
| 方法 | 直接去除词缀 | 通过词典分析得到词根 |
| 效果 | 速度快,准确率低 | 速度慢,准确率高 |
| 适用场景 | 快速处理,例如信息检索 | 精确分析,例如文本翻译 |
例如:对于单词happily,词干提取的结果是happi(去掉了后缀-ly),而词法分析的结果为happy(考虑了词典中的词根)。
以词干提取为例:
from nltk.stem import PorterStemmer
stemmer = PorterStemmer()
def stem_tokens(tokens):
stemmed = [stemmer.stem(word) for word in tokens]
return stemmed
tokens = stem_tokens(filtered_tokens)
print(tokens)
1.2 词嵌入(word2vec)
词嵌入(word to vector),使用于表示词语意义的向量;将单词映射到实向量的技术称为词嵌入。这些向量可以更好的表达不同词之间的相似度和类比关系;
由于独热向量表示的单词之间的余弦相似度为0,所以独热向量不能对词之间的相似度进行编码。word2vec包含如下两个常用自监督模型来进行词嵌入。
word2vec模型的优点:提供稠密的向量表示,捕捉词语的语义关系。word2vec将每一个词都表示成一个稠密向量;对于两个单词对应的词向量,它们的距离大小可以衡量它们的语义相似性(单词在意义上的接近程度;距离越近,语义相似性越高),而它们的夹角大小可以用来衡量语义关联性(两个单词在语境中的共现关系;夹角越小,关联越强大)。
1.2.1 跳元模型(skip-gram)
跳元模型假设一个词可以用来在文本序列中生成其周围的词;
给定中心词,跳元模型考虑生成上下文词的条件概率:
在此模型中,每个单词都有两个向量表示其用作中心词和上下文词时的两个向量。对于单词w(i),其中心词向量为vi,上下文词向量为ui。
给定中心词w(c),生成任何上下文词w(o)的条件概率可以使用对向量点积的softmax操作来建模:
p(w(o)|w(c)) = exp(Uo^T@Vc) / ∑exp(Ui^T@Vc);
跳元模型的似然函数为:给定任何中心词的情况下生成所有上下文词的概率。
跳元模型的训练为极大似然估计MLE方法,并使用随机梯度下降来求得最优解。在对词表中的词w(i)进行训练后,得到其作为中心词与作为上下文单词这两个词向量;在NLP的应用中,跳元模型的中心词向量通常作为词的表示向量。
1.2.2 连续词袋模型(CBOW)
CBOW和跳元模型恰好相反;其假设中心词是基于上下文词生成的。
在基于上下文词之上,CBOW模型考虑生成中心词的条件概率。
不同点在于由于存在多个上下文词,因此在计算条件概率时需要对这些上下文词向量进行平均;假设对于词w(i),其上下文词和中心词向量为Vi和Ui,给定上下文词 Wo={w1,...,wo},还给定这些词的上下文词向量均值 Vo(bar) = 1/o(V1+...+Vo)时,生成任意中心词W(c)的条件概率可以表示为
p(w(c)|W(o)) = exp(Uc^T@Vo(bar)) / ∑exp(Ui^T@Vo(bar));
CBOW的似然函数是在给定其上下文词的情况下生成所有中心词的条件概率。
总结:跳元模型求给定中心词生成上下文的条件概率,连续词袋模型求给定上下文生成中心词的条件概率。
1.2.3 近似训练
由于word2vec方法得到的似然估计的梯度包含了求和操作,对于一个单词较多的词表计算开销太大。所以引入近似训练的方法:
第一种称为负采样,其修改了目标函数为给定中心词与其上下文窗口,任意上下文词来自该中心词的上下文窗口的条件概率:点积后加入sigmoid激活函数。
之后,从最大化文本序列中所有这些事件的联合概率开始训练词嵌入。考虑最大化联合概率时为了使目标函数有意义,故从预定义分本中采样一些不是来自这个上下文窗口的噪声词,称为负样本。
这样计算后得到的对数损失在每个训练步上的计算成本就与词表大小无关了。
第二种方法为层序softmax。
层序softmax使用了二叉树的结构,树的每个叶节点表示词表中的一个单词。以跳元模型为例,给定一个中心词来生成另一个单词的条件概率需要从根节点到此单词路径上所有非叶节点向量之间的点积;由于使用了二叉树,层序softmax的时间也被大大缩短了。
1.2.4 总结
| 特性 | 跳元模型 | 连续词袋模型 |
| 预测目标 | 给定中心词预测上下文 | 给定上下文预测中心词 |
| 训练速度 | 较慢 | 较快 |
| 数据需求 | 大规模效果好 | 小规模效果好 |
| 上下文窗口大小 | 较大,捕捉更广泛的上下文关系 | 较小,捕捉局部上下文关系 |
| 捕捉能力 | 对稀有词效果好,捕捉单词语义关系 | 对常见词效果好,捕捉词频信息 |
1.3 注意力(Attention)
1.3.1 注意力机制
注意力机制是一种允许模型在处理序列数据时,使用注意力计算来灵活的关注序列不同部分的方法;注意力机制通过计算序列中每个元素对其他所有元素的注意力权重来处理序列数据。
注意力机制由双组件构成:非自主提示和自主提示;在接受输入的过程中,称自主提示为查询(Query),非自主提示为键(Key),每个键会对应一个值(Value,类似于感官反应)。在输入双组件后,经由注意力汇聚得到最终的输出;
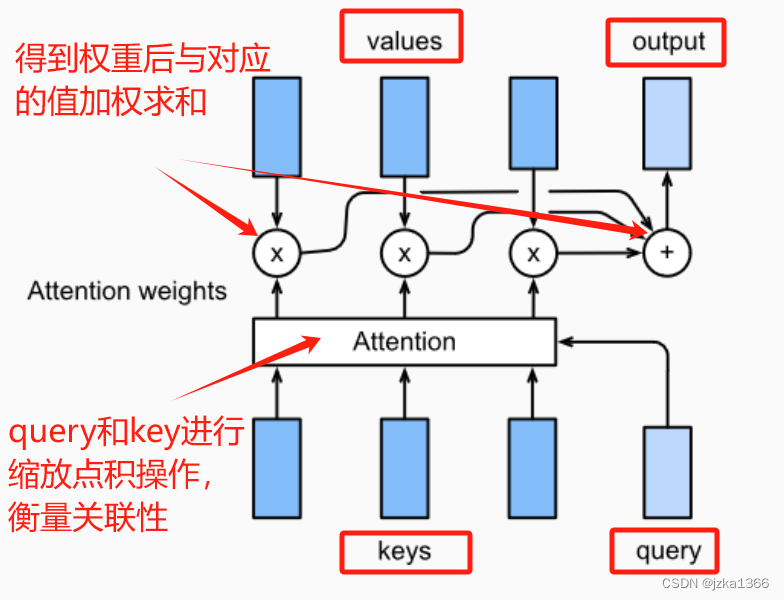
具体来说,键和其值是原本就存储在模型当中的;每次输入一个查询,这个查询与每个键都经过一个统一设置的注意力评分函数(Scoring function);这个评分函数类似于SVM中的核,可以简单的使用点积 Q*K^T 来衡量询问和键之间的相关程度,也可以使用高斯核等衡量方法。其次,对这些查询和键之间的相关性得分应用 Softmax 函数来得到一个概率分布。(这保证了对于任意查询,所有键值对注意力权重均为概率分布)。最后将每个概率分别乘以它所对应的值,加权求和后即得到输出。
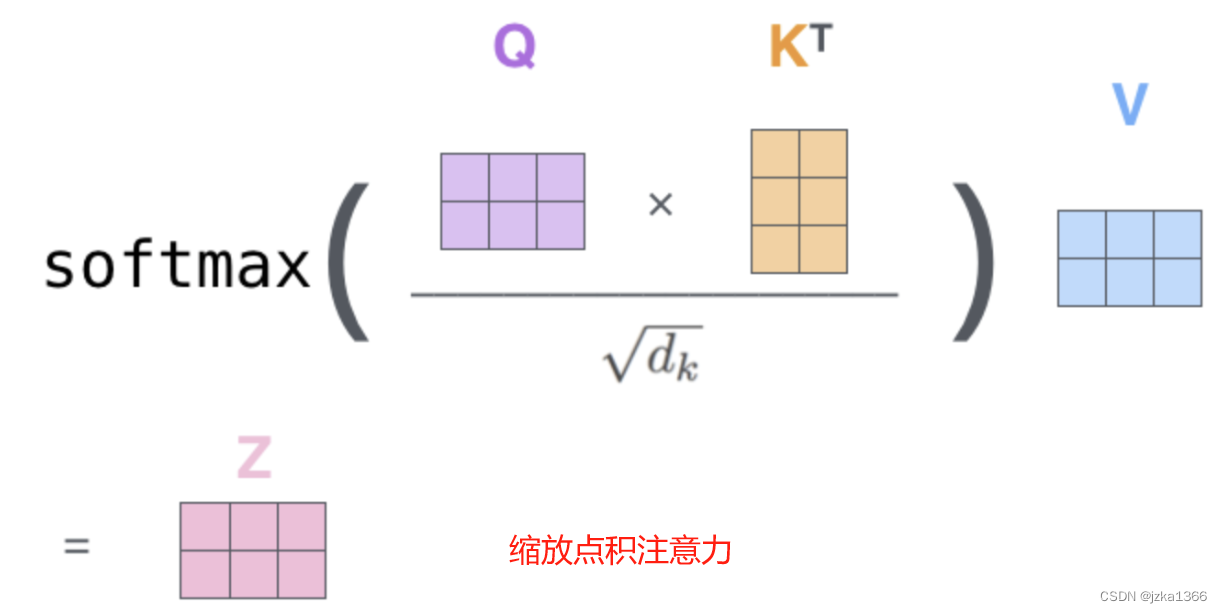
换句话说,每个询问和键相比对,越相似的键权重越大,询问的值自然就与这样的键越相似。
1.3.2 多头注意力
核心思想:通过并行计算多个注意力机制/头,来捕捉不同子空间的信息,并将这些信息整合。
多头注意力将输入的查询,键,值数据,通过多个并行的注意力头进行处理;每个注意力头可以关注不同的子空间,从而增强模型的表示能力;
具体步骤:
首先将输入的Q,K,V向量分别通过独立的线性变换层来生成多个不同的向量组;再将这些不同的向量组存储到不同的注意力头之中。其次,对于每个头,独立计算注意力:
Head(i) = Attention(Qi, Ki, Vi) = Softmax(Qi * Ki^T / d) * Vi
(先点积求关联,再分成概率,加权求和)。
【*】:原式中除以维度d的步骤称为缩放点积注意力,目的是为了防止注意力权重的极端值,使梯度更稳定。
最后拼接所有的头在一起,并再进行一次线性变换后输出
MultiHead(Q,K,V) = Concat(Head1,...,Head(h)) * W(o)(先拼接,再乘以线性变换矩阵)。
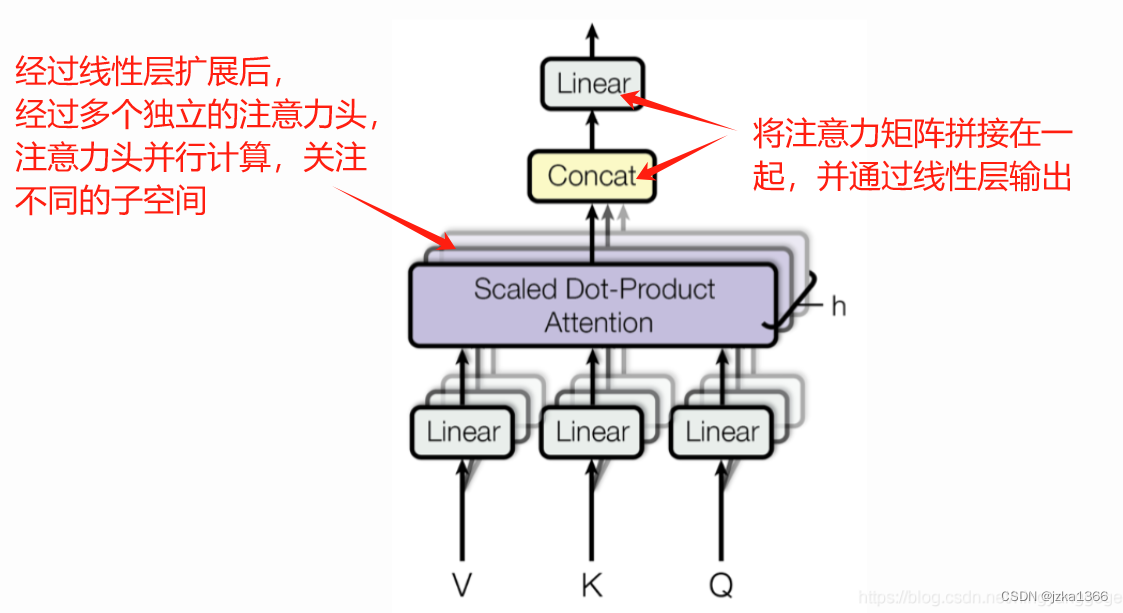
优点:
可以并行计算,节省时间;其次,多头注意力结构可以关注数据的不同方面,捕捉多样化特征;例如在机器翻译中,允许解码器在生成每个单词的时候动态的关注源句子中的不同部分,捕捉上下文信息。
1.3.3 自注意力
自注意力是注意力机制的一种特殊形式,主要用于序列建模任务中。它通过同一序列内不同位置间建立依赖关系,使模型灵活关注序列不同部分。
核心思想:
通过对同一序列中所有元素进行相互注意力计算,来生成每个元素的上下文表示。它可以在序列中捕捉长距离的依赖关系。
有了注意力机制后,将词元序列输入到注意力汇聚中,同一组词源同时充当查询,键,和值;每个查询都会关注所有的键值对并生成一个注意力输出。最后这步加权求和可看作对于每一对词的表示计算一个打分,表示一个词对另一个词的重要性。
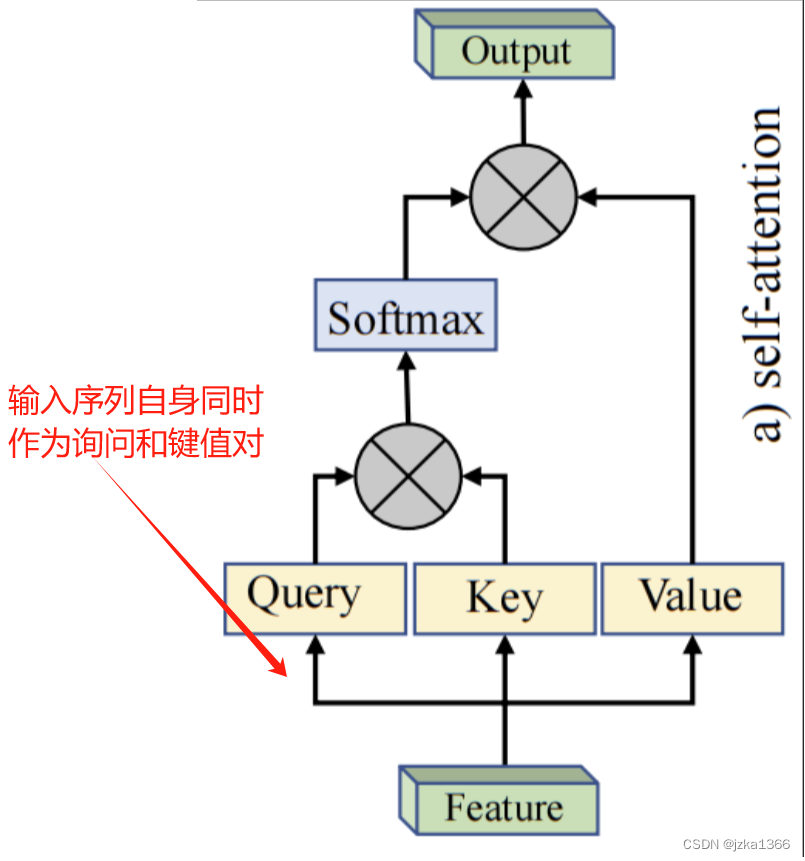
主要步骤:
以NLP处理为例,给定一个输入序列 {x1,...,xn},每个输入xi通常是一个词的嵌入向量;
首先,输入序列中的每个向量都被投影到查询,键,和值这三个不同的向量空间。这通过与三个不同的权重矩阵 Wq, Wk, Wv进行线性变换来实现:Q = XWq, K=XWk, V=XWv;这些权重矩阵可以在训练过程中学习。
其次,计算每组QKV的注意力之值:按照一般做法(例如点积核)衡量相似度,然后通过Softmax进行归一化。最后,将注意力权重对值向量进行加权求和,得到自注意力的输出。
1.3.4 位置编码
在处理词元序列时,RNN是逐个重复的处理词源的;而自注意力机制则因为并行计算而放弃了顺序操作;为了使用序列的顺序信息,通过在输入表示中添加位置编码(positional encoding)来注入位置信息。位置编码可以通过学习得到,也可以直接固定,例如常用的基于正余弦的固定位置编码。
1.3.5 Transformer模型
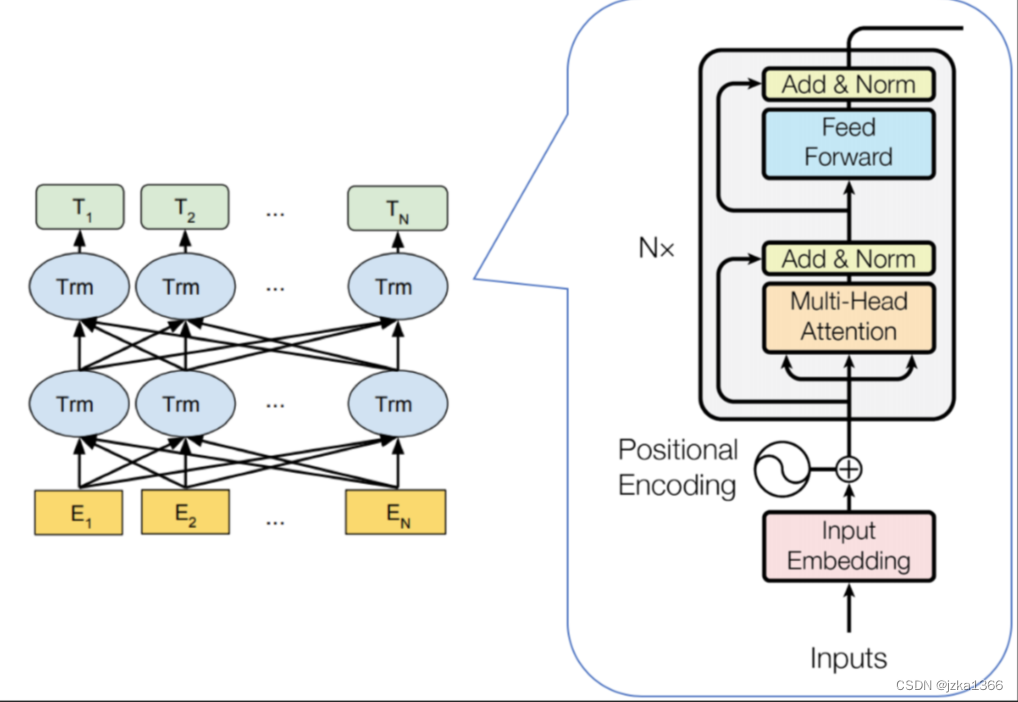
Transformer模型是一种完全基于自注意力机制的深度学习模型;它完全抛弃了循环和卷积结构,完全基于自注意力机制,使其能够更高效地处理长距离依赖关系。Transformer模型主要由编码器核解码器两个部分组成,每个部分由多个相同的层堆叠而成。
编码器:
每个编码其首先计算MultiHead(Q,K,V),使用多头自注意力机制来关注输入序列的不同部分;
其次进入前馈神经网络(FNN),每个位置向量通过一个前馈神经网络进行独立的非线性变换:FFN(x) = ReLU(xW1+b1)W2+b2;
此外,每个子层后都要经过层归一化和残差连接,帮助训练更深刻的模型。
解码器:
与编码器类似,首先使用掩码多头自注意力机制(Masked Multi-Head Self-Attention):某些文本序列被填充成其他信息;这是为了防止解码器在生成下一个词的时候看到未来的信息。
其次再使用多头交叉注意力机制,将解码器的查询与编码器的键值向量进行注意力计算,使解码器能够访问编码器的输出。最后经过前馈神经网络和层归一化与残差连接,与编码器类似。
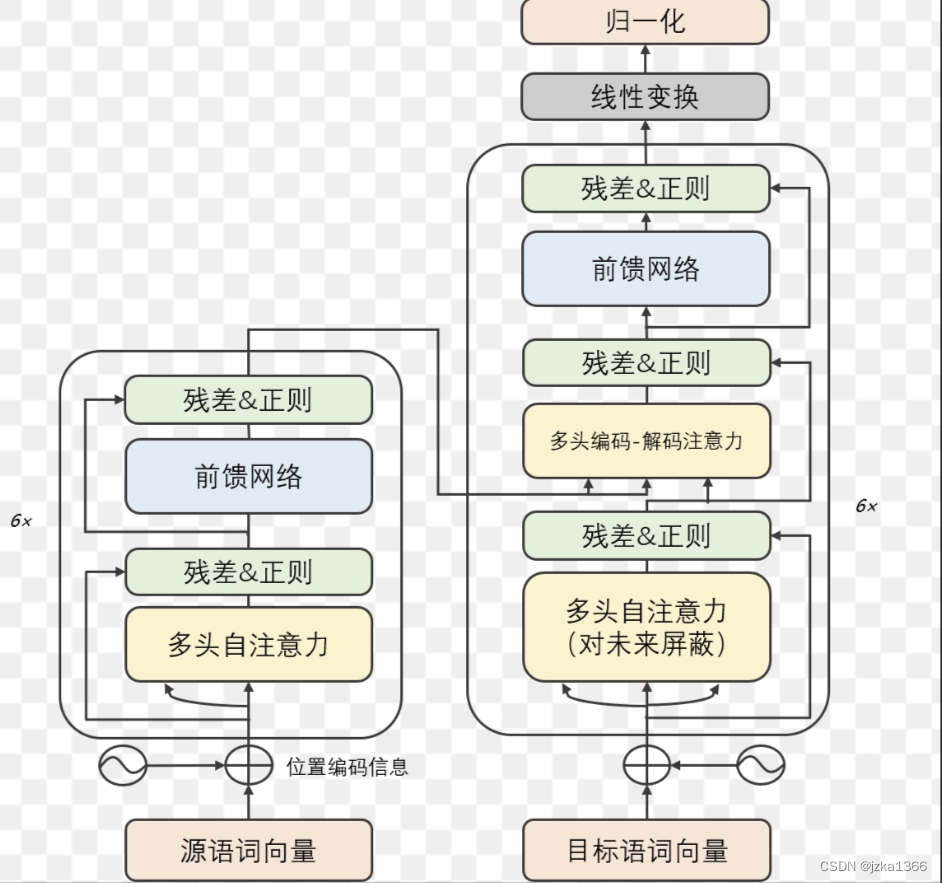
输入和输出同时输入解码器的多头注意力机制的设计,确保了解码器能够利用编码器提供的上下文信息,以及自身生成的部分序列,来准确生成目标序列。这部分机制使解码器在生成每个新词时,可以访问和利用编码器的上下文信息(即原始输入序列的表示)。这样,解码器能够在生成翻译(或任何输出序列)时,更加准确地参照输入序列;这种设计被称为教师强制。
然而,在推理期间,解码器不能访问完整的目标序列。相反,它必须逐步生成序列,用自回归的方式利用前一步生成的词作为下一步的输入。

模型训练:
Transformer使用自注意力和前馈神经网络处理输入输出序列,使用交叉熵损失来优化模型参数;
模型优点:
并行计算;能够之间建模任意两个位置的依赖关系;灵活扩展性
模型应用:
机器翻译,文本生成,问答系统,图像处理;
【*】一些特殊的Transformer模型:
双向Transformer架构:运用在BERT模型中;双向架构能同时考虑前后文信息,提高语言理解能力。
多模态Transformer:通过自注意力机制在不同模态之间建立联系,捕捉跨模态的特征和关系。
1.4 语言模型
语言模型是一种能够理解和生成自然语言文本的统计模型;
语言模型的目标是预测句子中的下一个词,也可以说是估计序列的联合概率;联合概率可以分解为条件概率的乘积;
为了训练语言模型,需要计算单词出现的概率,以及给定单词后出现某个单词的条件概率;这些概率本质上就是模型的参数。
单词的词频满足奇普夫(Zipf)定律,即第i个最常用的单词的频率n(i)满足n(i)正比于1/i^a;其中a是描述分布的指数。
衡量模型的质量:可以计算n个词元的交叉熵损失的平均值来衡量;交叉熵损失能够测量预测概率分布与真实分布之间的差异。
将其取成exp的指数得到的值被称为困惑度(perplexity),其解释为下一个词元的实际选择数的调和平均数。
1.4.1 基础模型
1. n-gram 模型:
通过统计固定长度的词序列(如三元组)的频率来估计下一个词的概率;
优点:易于实现;缺点:无法捕捉长距离依赖关系。
2. 基于神经网络的语言模型:
前馈神经网络能够捕捉词语之间的非线性关系,但其无法处理变长序列;
由RNN实现的语言模型利用隐状态传递信息,能够处理变长序列,能够捕捉长距离依赖关系;然而其训练时会存在梯度消失或梯度爆炸的问题。
用LSTM或GRU改进过后的RNN引入了门控机制解决了梯度问题,还能够更好的捕捉长距离依赖关系,然而结构复杂,计算开销较大。
3. Transformer语言模型:
通过自注意力机制处理序列数据,可以更高效且并行化的处理长序列和全局依赖关系。
1.4.2 模型组件和步骤
1. 词嵌入(Word Embeddings)
将词语表示成固定维度的向量,使得语意相近的词在向量空间中距离相近;常用方法有Word2Vec;在神经网络模型中,则是通过嵌入层将词转换为向量;
2. 模型结构
输入层:接受文本序列,通常是嵌入向量;
隐藏层:通过GRU或是Transformer结构模型处理序列数据,捕捉上下文信息;
输出层:通过Softmax函数输出每个词的概率分布,用于预测下一个词。
3. 训练过程
目标函数:通常使用交叉熵函数,最大化训练数据的概率;
优化算法:Adam
正则化技术:常用的有Dropout和权重权重衰减,防止过拟合。
4. 模型评估
对于语言模型性能,通常使用困惑度(Perplexity)衡量;其表示模型对于测试集进行预测的难易程度;困惑度越低,模型性能越好;公式为exp(交叉熵均值)。
在机器翻译等生成任务中,还会使用BLEU分数评估生成文本与参考文本的相似性。分数越接近1,说明翻译效果越好。
总结:BLEU用于评价生成文本与参考文本的相似性,困惑度用于评语言模型的预测能力。
1.4.3 高级模型
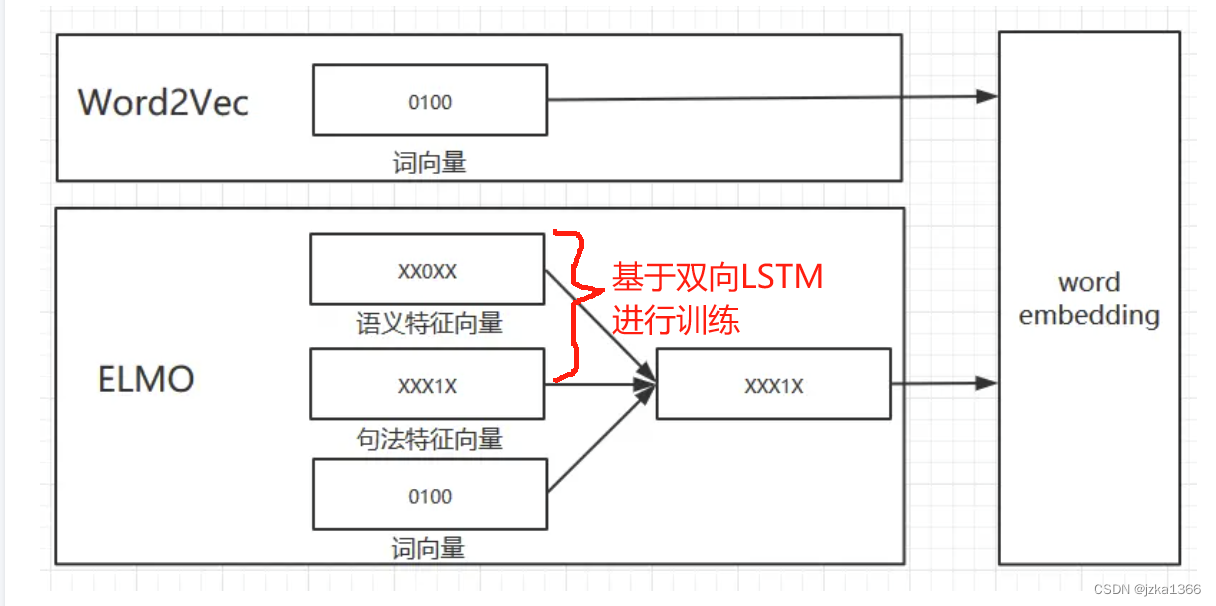
1. ELMo--来自语言模型的嵌入
定义:其是一个预训练的语言表示模型,旨在生成上下文敏感的词向量表示。
原理:词语通过双向长短期记忆网络(BiLSTM),对于句子按照正反的两种顺序进行处理,从而生成上下文敏感的词向量(即对上下文进行双向编码);这种上下文敏感的词向量表示能够捕捉词语在不同语境下的多义性和复杂语义关系。
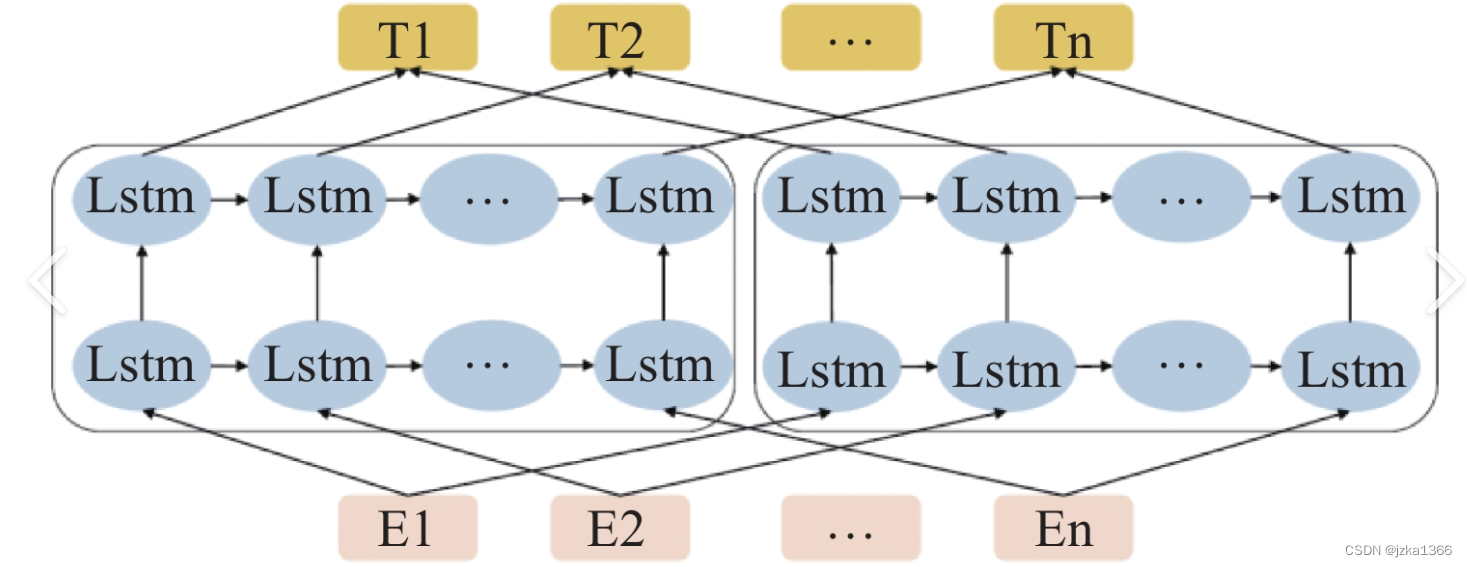
应用:显著提升NLP任务的性能。
2. GPT--生成式预训练
定义:生成式预训练变换器,使用单向Transformer进行语言建模,擅长生成文本;
GPT模型为上下文敏感表示设计了通用的任务无关模型。GPT完全建立在Transformer解码器的基础之上,预训练了一个用于表示文本序列的语言模型。在文本生成时,GPT模型通过逐步预测下一个词,并将预测的词作为输入逐步迭代生成完整的句子或段落。然而,由于语言模型的自回归特性,GPT只能从左到右读取词元。
原理:
在预训练阶段,GPT在大规模的文本数据上进行语言模型预训练,任务通常为自回归语言模型,即预测下一个此的概率。具体来说,给定一个词序列,GPT学习如何生成下一个词,从而在语料库中捕捉语言模式和知识。其次,在特定任务数据上进行微调,使其适应具体的任务要求。
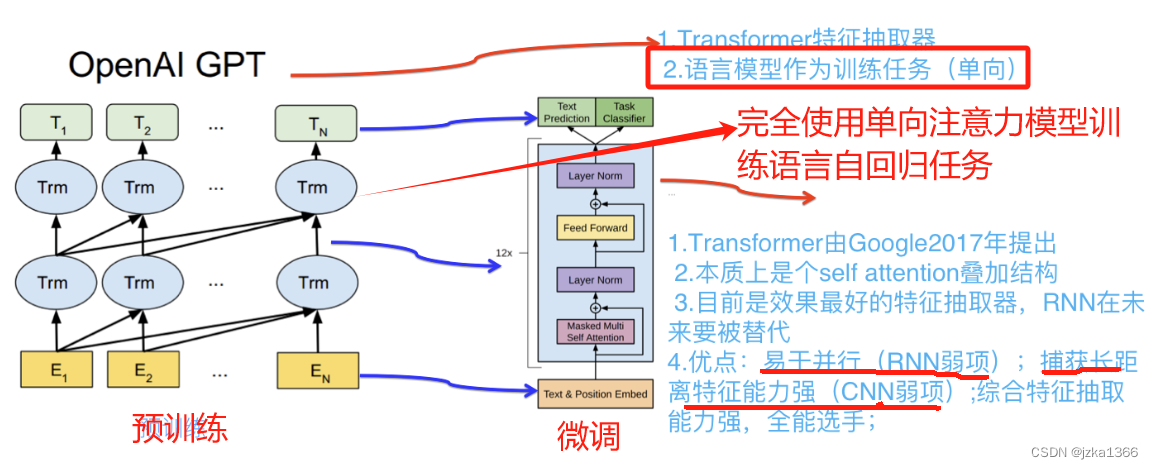
应用:生成连贯的问本并进行建模;下游任务包括了对话系统,文本生成等。
3. BERT-双向编码表示器
定义:双向编码器表示器,使用双向Transformer进行预训练,擅长理解与生成上下文相关的文本。
ELMO是分别看上文和下文,然后将上文得到的结果和下文得到的结果进行拼接。而BERT是同时看上下文中的每个词而进行推断。
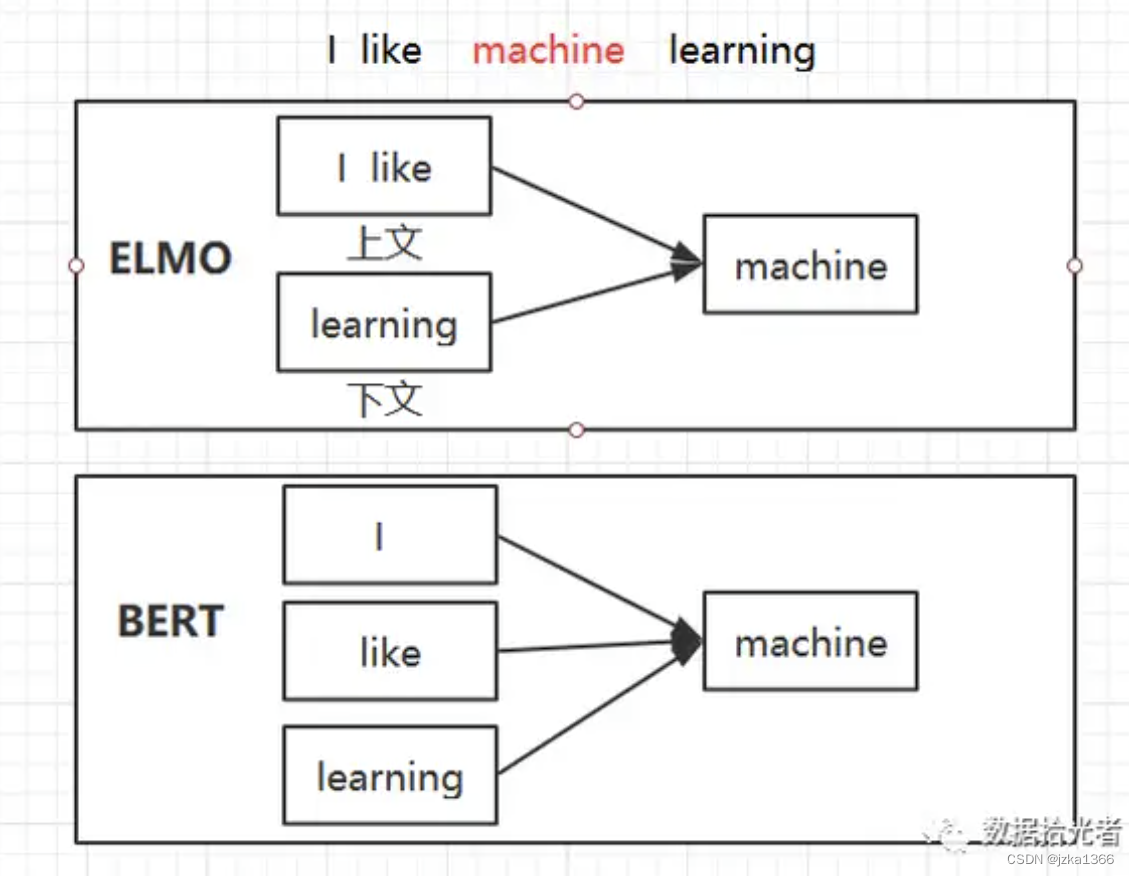
主要特点:
1. 双向编码表示:BERT通过同时考虑上下文中所有的词,进行双向的训练,从而更好地捕捉到词语的上下文信息。
2. 预训练和微调:BERT首先在大规模无监督文本数据上进行预训练,使用掩码语言模型(MLM)【*】以及下一句预测模型(NSP)【**】预训练模型。在与训练之后,BERT再在特定任务数据上进行微调。
【*】:MLM随机掩盖输入文本中的一些词,并训练模型预测这些词;这种方式是的模型能够从上下文中学习词语的表示。
【**】:NSP可以训练模型预测两短句子是否是连续的,从而使得模型能够理解句子之间的关系。
应用:理解上下文并执行NLP的大部分任务;例如文本分类,情感分析,NER等。。
1.4.4 总结
对于三个高级模型的总结:
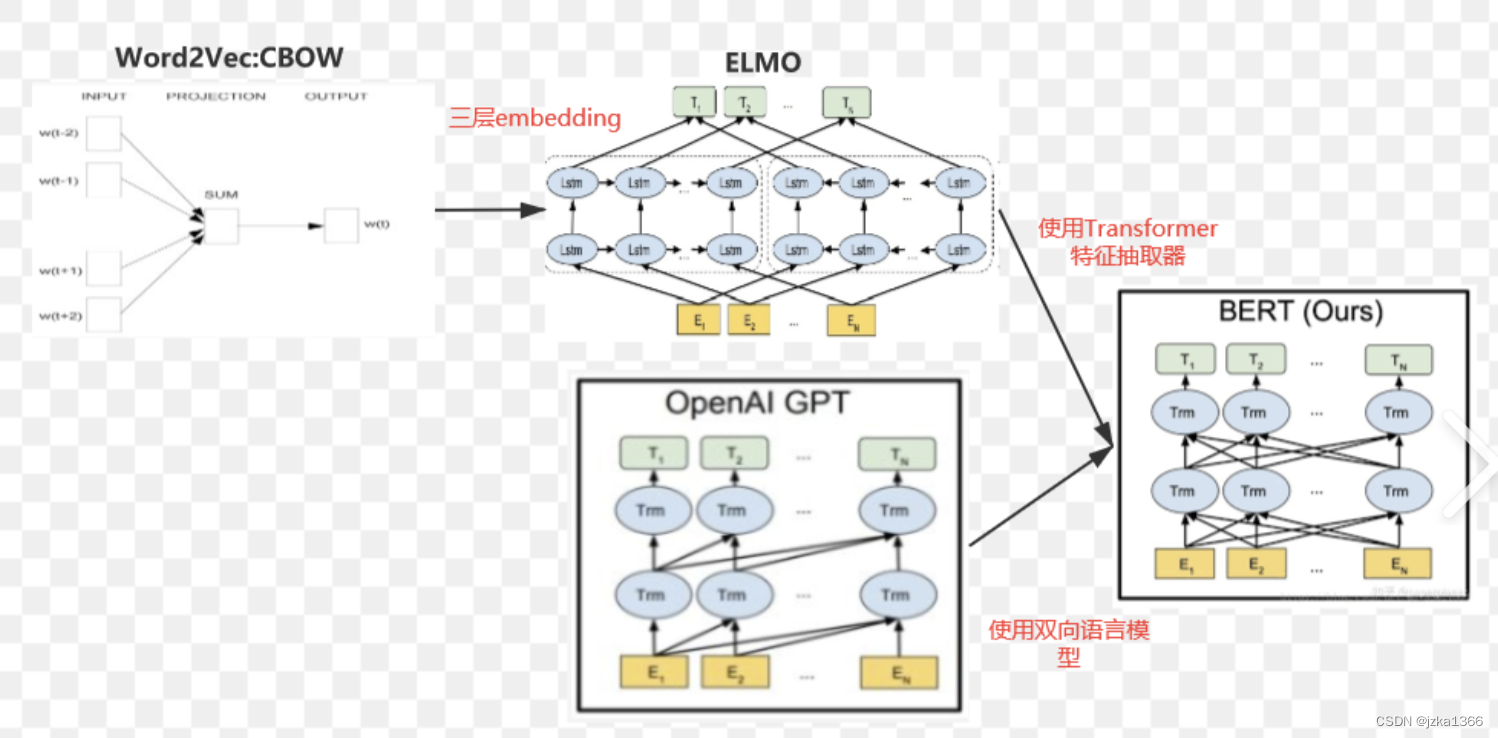
对于词向量,使用BiLSTM进一步得到句法和语义向量,就把word2vec的CBOW模型(基于上下文生成中心词)改为了ELMO模型;而将ELMO模型中的基于RNN的LSTM改为基于注意力的Transformer抽取特征,那么ELMO模型就被改成了BERT模型。
另一方面,将单向Transformer实现的GPT模型改为双向实现,也会变为BERT模型。
对于所有适用于语言任务的模型总结表:
| 特性 | n-gram模型 | 神经网路模型 | 预训练模型 |
| 原理 | 统计固定长度词序列的频率 | 神经网络捕捉上下文关系 | 预训练模型,在具体任务上微调 |
| 上下文 | 固定长度窗口 | 捕捉长距离依赖 | 捕捉长距离依赖 |
| 训练数据要求 | 中等,依赖于n的大小 | 大量数据 | 超大规模的数据 |
| 代表模型 | 二元,三元模型 | GRU, Transformer | GPT, BERT |
| 应用场景 | 文本预测 | 翻译,分类 | 问答,生成 |
| 优点 | 简单,计算效率高 | 处理复杂上下文,表达能力强 | 迁移学习效果最好,表现最佳 |
| 缺点 | 上下文有限,参数爆炸 | 训练复杂度高 | 训练耗时耗资源 |
1.4.5 大语言模型(LLM)
大语言模型是指在大量文本数据上训练的语言模型,能够理解和生成自然语言文本。这些模型通常由数以亿计的参数,并且通过复杂的神经网络架构捕捉语言的差别和复杂性。
工作原理:
LLM通常使用Transformer架构,通过自注意力机制处理输入序列,并生成输出序列。
首先是预训练步骤,LLM在大规模未标注的文本数据上进行无监督学习,并通过预测掩码词【1】或预测下一个词【2】来学习语言基本结构和规律。
【1】:掩码语言建模(MLM),指在BERT中随机掩码一些词,模型尝试预测这些被掩码的词;
【2】:自回归语言建模:在GPT中,模型根据前面的词预测下一个词。
其次是微调(fine tunning):在特定任务或领域的小规模标注上进行监督学习,使模型适应具体任务,例如文本分类或问答系统。
1.5 具体任务
1.5.1 文本分类
任务定义:将文本数据分配到预定义的种类中;
常用算法:BERT
原理:
BERT基于Transformer,在预训练时通过遮蔽词和预测下一句句子来学习语言的上下文表示;在文本分类任务中,使用特定任务的数据集来对预训练好的BERT进行微调*即可。
【*】微调的过程:
将待分类的文本输入到BERT模型中,提取与序列标记对应的隐藏状态,用向量表示文本的语义。再将提取出的向量输入一个简单的全连接神经网络进行分类,输出每个类别的概率分布。
1.5.2 情感分析
任务定义:判断文本中表达的情感极性;
常用算法:LSTM
原理:
将待分析的文本序列化后输入LSTM网络,LSTM通过单元门控机制对序列进行处理,每一个时间步都产生一个隐藏状态;最后时间步的隐藏状态用作文本的整体并表示,将其输入全连接层进行分类,输出情感的概率分布。
1.5.3 命名体识别(NER)
任务定义:从文本中识别并分类出具有特定意义的实体,如人名地名时间等;
常用算法:CRF
原理:
1. 序列标注:使用词向量表示出文本中的每个词,再使用CRF进行序列标注:考虑标记序列的全局最优性,通过最大化条件概率来进行预测。
2. 特征函数:定义特征函数来表示词与标签之间的关系。
3. 解码:使用维特比算法进行解码,找到最可能的标签序列。
1.5.4 机器翻译
任务定义:将文本从一种语言自动翻译成另一种语言;
常用算法:Transformer
原理:
使用编码器将词向量经过多头自注意力机制输入到解码器中进行解码。编码器将源语言转换为上下文表示,解码器根据这个表示生成目标语言序列。
1.5.5 问答系统
任务定义:从给定的文本中自动回答用户提出的问题;
常用算法:BERT
原理:
BERT使用双线性层,对于段落中的每个词预测其作为答案的起始位置和结束位置的概率。通过两个独立的线性层分别计算起始和结束位置的分数。
再通过softmax函数将分数转化为概率分布,最后选择使得起始结束位置概率乘积最大的词作为答案边界。
1.5.6 语音识别
间第3.2节语音识别部分内容。
1.5.7 摘要生成
任务定义:将长文本浓缩成简短的摘要;
常用算法:注意力机制实现的Seq2Seq模型
原理:
1. 编码:使用LSTM编码器将输入文本编码成固定长度的上下文向量;
2. 注意力计算:计算当前隐藏状态与编码器隐藏状态的相关性并生成注意力权重;
3. 解码:解码器在生成摘要时,结合上下文向量和注意力权重计算出的加权和来生成词语;
4. 生成:通过搜索算法生成最终的摘要序列。
1.5.8 词性标注
任务定义:为句子中的每个词分配适当的词性标签;
常用算法:双向LSTM+CRF
原理:
使用双向LSTM处理输入的词序列,再进行特征表示;在LSTM的输出上连接一个CRF层,考虑标签之间的依赖关系,进行全局最优的序列标注。最后使用维特比算法解码出最可能的词性标签序列。
2. 计算机视觉(CV)
2.1 图像增广
图像增广指对训练图像进行一系列的随机变化之后,生成相似但不同的训练样本;这样的操作可以减少模型对于某些属性的依赖,从而提高模型的泛化能力。
常用的图像增广方法有翻转,裁剪,和改变颜色。
2.2 特征提取
特征提取旨在原始图像数据中提取出描述性的信息,以便接下来的分类,检测,识别等任务。
定义:特征提取是将原始图像数据转化为更容易处理和理解的特征向量的过程。
目的:降维(高维数据将位至低维向量),去冗余,增强区分性。
步骤:
首先对图像进行预处理(转化为灰度图,归一化像素值);其次选择特征并应用相应的算法进行提取。最后使用PCA等方法对特征向量进行降维处理。
1. 颜色特征
对于颜色特征的提取,可以使用颜色直方图统计图像中每种颜色出现的频率(常用于图像检索和相似度计算);或采用颜色空间变换,将RGB颜色空间转换为LAB等。
2. 纹理特征
对于纹理特征的提取,可以使用描述灰度级联合分布的灰度共生矩阵或通过比较像素之间的灰度值的局部二值模式来进行提取。
3. 形状特征
形状特征的提取可以采用:基于边缘检测算子提取图像的边缘信息,或基于变换算法提取图像中的几何形状和轮廓。
4. 其他特征
其他特征包括局部特征和深度学习特征,可以使用预训练的卷积神经网络进行提取。
2.3 目标检测
目标检测(或目标识别)的任务是在图像或视频中识别目标的类别与它们在图像中的具体位置。
其被广泛应用在自动驾驶,监控及医疗影像当中。
在目标检测任务中,分类与回归任务通常结合在一起进行。因此模型通常使用多任务损失函数。
2.3.1 锚框
在目标检测中,通常使用边界框(bounding box)来表述目标的空间位置。目标检测算法通常会在输入图像中抽取大量区域,然后判断区域中是否包含目标,从而调整边界而更准确的预测真实边界框。
以每个像素为中心,生成多个缩放比和宽高比不同的边界框,这些边界框被称为锚框(anchor box)。
衡量锚框和真实边界框的相似性可以用杰卡德相似系数衡量。给定集合A和B,他们的杰卡德系数是它们交集的大小除以它们并集的大小:J(A,B)=|A∩B|/|A∪B|;对于锚框和真实边界框,它们框内的像素可被看作是集合的元素,它们的杰卡德相似系数又称为交并比(IoU)。IoU的取值范围在0到1之间,0表示边框无重合像素,1表示两个边界框完全重合。
在训练集中,将每个锚框视为一个训练样本。为了训练目标检测模型,需要标注每个锚框的类别和偏移量标签;其中偏移量代表锚框和真是边框的偏离大小。
多尺度锚框:
若为每个像素都生成一个锚框,最终的锚框数量过多需要过多时间。为了解决这样的问题可以使用多尺度锚框:在输入图像中均匀抽样一小部分像素,并以它们为中心生成锚框。当使用较小的锚框检测较小的目标时,可以抽样较多的区域;而对于较大的目标,可以抽样较少的区域。
2.3.2 非极大值抑制(NMS)
当有许多锚框时,为了简化输出避免重合率过高,可以使用非极大值抑制算法合并属于同一目标的相似的预测边框。其模型原理如下:
目标检测模型会计算每个类别的预测概率,这些预测概率称为置信度。首先将所有置信度降序排序,每次选取最大的置信度,将所有与此概率对应的边界框的IoU值超过一定阈值的边界框删除;按降序遍历所有置信度和对应的边界框,最后可以得到的集合中任意一对边界框的IoU都小于阈值(即没有一对过于相似)。
2.3.3 单发多框检测(SSD)
SSD通过卷积神经网络提取图像特征,并在不同层上进行目标检测,从而实现高效、准确的多目标检测。其主要由一个基础网络快和数个多尺度特征块组成。基础网络块可以使用CNN从输入图像中提取特征,而多尺度特征块用来检测目标:第一个特征快的高和宽较大,可以检测到较小的目标;接下来每一个特征块都将上一层的高和宽缩小来进行检测。
2.3.4 区域卷积神经网络(R-CNN)系列
区域卷积神经网络R-CNN系列是将深度模型应用于目标检测的开创性工作。
1. R-CNN
R-CNN首先从输入图像中选取若干个提议区域(如锚框)并标注他们的类别和边界框以及边界框的偏移量;然后,用CNN对每个提议区域进行前向传播以提取具体特征。最后训练SVM进行类别预测,训练线性回归进行边框预测。
缺点:每个CNN独立,时间开销巨大。
2. Fast R-CNN
为了解决R-CNN的问题,快速R-CNN做出了改进:仅在整张输入图片上执行卷积操作与前向传播;
此外,快速R-CNN还引入了兴趣区域汇聚层(ROI池化),其将CNN的输出与提议区域合并作为输入,输出链接后的各个提议区域的特征。
缺点:在选择性搜索中需要生成大量的提议区域。
3. Faster R-CNN
更快速的R-CNN将选择性搜索替换为使用了卷积层预测锚框的区域提议网络(RPN)而其余结构保持不变。
作为端到端的训练结果,区域提议网络能够学习如何生成高质量的提议区域。
总结:
| 特性 | R-CNN | Fast R-CNN | Faster R-CNN |
| 候选区域 | 选择性搜索 | 选择性搜索 | 区域提议网络RPN |
| 特征提取 | 单独提取 | 共享特征图 | 共享特征图 |
| ROI池化 | 不使用 | 使用 | 使用 |
| 分类回归 | SVM+线性回归 | 全连接层 | 全连接层 |
| 训练阶段 | 多阶段 | 单阶段 | 单阶段 |
| 检测速度 | 很慢 | 快 | 很快 |
| 优点 | 精度高 | 效率高 | 端到端 |
| 缺点 | 计算开销大 | 候选区域生成慢 | 复杂性增加 |
4. Mask R-CNN
掩码R-CNN在更快的R-CNN上继续做出改进,将兴趣区域汇聚层替换为了兴趣区域对齐。
2.3.5 YOLO模型
You only look once, YOLO模型使用了单阶段检测,直接从图像中预测边框和类别。
2.4 分割问题(Segmentation)
分割问题旨在将图像按照某种规则划分成不同的区域。应用如医学影像处理,自动驾驶,自然场景理解等。
2.4.1 图像分割
图像分割指将图像划分为若干区域,每个区域内部具有相似属性,如颜色纹理等。
例如:将一张卫星地图划分为水体,植被和城市区域。
常用算法:
使用K-means聚类,将像素堪称特征向量(如颜色,位置);再使用聚类算法将像素聚类成为k个簇,每个簇对应一个图像区域。
或者可以使用图论中的最小割算法,将像素空间建模位图,边表示像素之间的相似性;最后使隔开的边权重最小来划分区域;其他算法还包括使用EM算法实现高斯混合模型GMM。
2.4.2 语义分割
语义分割是指对图像中的每个像素进行分类,使得同一类的所有像素都被分到同一个类别中。
特点:每个像素被赋予一个类别标签;但只能区分类别,不能区分同一类别的不同实例。
例如,在一个城市街景图像中所有车辆的像素被标记为车辆,所有建筑物像素被标记为建筑。
常用算法:
最常用的算法为全卷积网络(FCN);其使用了CNN替换了全连接层,生成具有空间维度的特征图;再通过反卷积(上采样)层来将特征图恢复为原始图像分辨率;每个像素的类别由输出特征图的通道进行预测。缺点:边界不够精细。
其他的算法包括使用了编码器解码器架构,使用跳跃连接的UNet以及利用空洞卷积的Deeplab。
2.4.3 实例分割
实力分割不仅对图像中每个像素进行类别分类,还继续进行实例分类。每个像素都不仅被赋予一个类别标签,还拥有一个实例ID。
例如,在一个城市街景图像中不仅车辆像素被标记为车辆,还标记了是几号车辆。
常用算法:
使用掩码R-CNN可以同时进行目标检测以及实例分割,既输出边界框又输出分割掩码。
其他算法包括PANet以及TOLACT等。
总结:
| 特性 | 图像分割 | 语义分割 | 实例分割 |
| 目标 | 划分区域 | 像素分类 | 像素分类 |
| 标签种类 | 无标签 | 类别标签 | 类别+实例标签 |
| 复杂度 | 较低 | 中等 | 较高 |
| 应用 | 医学影像 | 自然场景理解 | 智能监控 |
| 算法 | 聚类 | FCN | Mask R-CNN |
3. 语音处理
3.1 语音信号处理(SSP)
语音信号处理是指对语音信号进行分析,修改和合成的技术方法。
其步骤如下:
1. 信号采集:
使用麦克风将语音信号转换为电信号;通过模拟-数字转换器(ADC)将其转换为数字信号。其目的为将声波转换为可处理的数字形式。
2. 预处理:
--预加重:高通滤波器通过增加高频成分来补偿发声过程中的高频损失;
--分帧和加窗:将连续的语音信号分割成短时帧,以便使语音信号在短时内平稳。常用的窗口又Hamming窗或矩形窗。
3. 特征提取:
常用的特征提取算法有:
基于快速傅里叶变换FFT和梅尔滤波器的梅尔频率倒谱系数(MFCC);优点:更接近人耳感知,缺点:对噪声敏感。
以及使用了线性预测分析的线性预测倒谱系数(LPCC);优点:复杂度低,缺点:表现不如MFCC。
4. 降噪和增强:
--语谱减法:通过减去背景噪声的频谱来降低噪声;
--维纳滤波:通过最小化MSE来增强语音信号。
3.2 语音识别
语音识别是将语音信号转换为文本的过程,使机器能够理解和处理人类语言;其核心为将连续的语音信号转化为离散的文字。
语音识别的步骤:
1. 预处理:进行语音信号采集和预处理(使用滤波器去噪和归一化等),减少噪声和无效部分;然后进行特征提取,使用频谱系数对频谱进行分析,提取倒谱特征。
2. 特征提取:利用例如梅尔频率倒谱系数或线性预测倒谱系数等方法,将原始的语音信号转换为特征向量,减少数据维度的同时突出关键信息;转化后的特征向量还可以经过标准化和时序建模等方法进一步捕捉特征。
3. 使用预训练的声学模型【*】进行解码,将输入的特征向量序列通过训练好的声学模型进行解码,得到音素序列或概率分布;
4. 使用预训练的语言模型【**】,结合声学模型的输出,对音素序列进行概率评估和重排序,得到最可能的文本输出;
5. 解码与输出:使用动态规划算法,例如维特比算法对声学模型和语言模型的联合概率进行解码,找到最优的词序列。
【*】预训练的声学模型:使用大规模的语音数据集,利用HMM,DNN等模型学习语音特征与音素之间的映射关系。
【**】预训练的语言模型:使用大规模的文本数据,利用n-gram或Transformer等模型学习词与词之间的概率关系和上下文依赖。
应用:语音助手,智能家居,语音输入等。
3.3 语音合成(T2S)
语音合成是将文本转换为语音的过程,使机器能够以人类语音的形式输出信息。
步骤如下:
1. 文本+音韵预处理:将输入的文本进行词法分析,分割成词元后再标注词性;之后将文本分块,进行句法和语义的分析,并标注重音和语调;再将单词划分为音节,标注音素音韵等。
2. 使用声学模型【*】,根据音素序列和韵律特征生成相应的语音波形;
3. 最后输出:将语音波形转化为音频格式,进行输出。
【*】:常见的声学模型包括:
1. 波形拼接:从预录制的音库中提取音素单元,根据目标音素序列拼接生成语音波形;
优点:生成的语音自然度高;缺点:需要大型音库。
2. 参数合成:通过HMM,DNN等模型生成语音参数,再合成语音波形;
优点:模型参数少易于调控;缺点:自然度较低。
3. 深度学习合成:使用深度神经网络,例如Tacotron直接学习并生成语音波形;
优点:自然度高,能够处理复杂特征;缺点:需要大量数据和资源。
4. 生成式人工智能(AIGC)
AIGC是指通过人工智能技术生成内容的过程。这些内容可以包括文本、图像、音频、视频等多种形式。AIGC的核心在于利用先进的机器学习算法,特别是深度学习技术,自动化地创建高质量、具有创意的内容。
其常用的生成模型包括GAN,RNN,GPT,BERT,CV,语音合成Tacotron等生成式模型。
应用实例:文本,图像,视频,音频的生成。
优点:高效,个性化,具有创意潜能;
缺点:需要质量控制,依赖于训练数据的质量,以及潜在的侵权问题。
5. 多模态(Multimodal)
多模态是指结合多种类型的数据(如文本,图像,音频,视频)进行分析和生成,充分利用不同模态的信息来提升AI系统的能力。
其步骤如下:
1. 数据收集与预处理:
获取多种模态的数据,并进行数据清洗以及数据同步:确保不同模态的数据再事件或内容上对齐;
2. 特征提取:
文本特征提取可使用TF-IDF或词嵌入;图像特征提取可使用CNN;音频特征提取可使用MFCC;视频特征提取可看作是图像加音频特征提取。
3. 特征融合:
早期融合--在特征提取阶段就将不同模态的特征融合,形成统一特征表示;
中期融合--在模型的中间层次进行特征融合,既考虑独立特征又保留模态之间的关联;
晚期融合--分别处理各模态的特征,最后才将各个模态的结果进行融合。
4. 模型训练:
根据任务选择例如联合深度学习,注意力机制等模型进行训练,使其能够有效利用多种模态的信息进行任务处理。
实际应用实例:情感分析,推荐系统,内容生成(AIGC)等。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








