从零开始-Machine Learning学习笔记(5)-神经网络

从零开始-Machine Learning学习笔记(5)-神经网络

0. 前言

​ 神经网络目前使用得最为广泛的定义是“神经网络是具有适应性的简单单元组成的广泛并行互连网络，它的组织能够模拟生物神经系统对真实世界级物体所作出的交互反应”。

​ 二十世纪四十年代M-P神经元模型、Hebb学习率，五十年代的感知机、Adaline等成果相继出现，迎来了神经网络发展的第一个高潮期。但是MIT的马文·闵斯基在1969年出版的《感知机》中指出单层的神经网络无法解决非线性问题，而多层网络的训练算法尚看不到希望，这个论断使神经网络进入了一段“冰河期”。

​ 1974年，Pual Werbos发明了BP算法，但此时正值神经网络的“冰河期”，并没有引起重视，直到1983年John Hopfiled利用神经网络，在旅行商问题的求解上获得了当时最好的结果，引起了轰动；紧接着Rumellhart重新发明了BP算法，在Hopfield带来的兴奋之下，BP算法迅速走红，神经网络迎来了第二次高潮。但是到了二十世纪九十年代中期，随着统计学习理论和支持向量机的兴起，神经网络学习的理论性质不够清楚、试错性强、在使用中充斥了大量的“窍门”的弱点更为明显，于是神经网络又陷入低谷。

​ 2010年前后，随着计算能力的迅速提升和大数据的涌现，神经网络的研究在“深度学习”的名义下重新崛起，迎来了第三次高潮。而我们目前就处于这波高潮的中心，充满了大量的挑战与机遇！

1. 神经元模型

​ 神经网络中最基本的成分是神经元模型，在生物神经网络中，每个神经元接受来自与其他神经元的信号，如果这些信号超过“阈值”，就会向其他的神经元发送信号。1943年，McCulloch与Pitts将上述的模型抽象成“M-P神经元模型”，如下所示：

神经元接收其它神经元传来的信号，并与“阈值”进行比较，并通过“激活函数”产生本神经元的输出。通常，理想情况下应该使用单位阶跃函数，但是单位阶跃函数不连续不光滑，所以在实际的使用中常常使用sigmiod函数来代替单位阶跃函数。

$$Sigmoid = \frac{1}{1+e^{-x}}$$

2. 感知机

​ 感知机由两层神经元组成如下图所示，输入层接受外部信号并传输给输入层，输出层是M-P神经元。其实就相当于在神经元的基础上，固定了神经元的输入。

通过感知机，我们可以轻松的实现与、或、非的运算。应注意到$y = f(\sum_iw_ix_i - \theta)$，假设我们这里取的f是单位阶跃函数，即大于0为1，小于0为0。那么根据与或非的逻辑运算规则，我们就可以很容易的写出权值：

与：$y = f(x_1 + x_2 - 1.5)$, 当$x_1$,$x_2$,均为1的时候，输出才为1，其余情况都是0

或：$y = f(x_1 + x_2 - 0.5)$, 当$x_1$,$x_2$,均为0的时候，输出才为0，其余情况都是1

非：$y = f(-0.6 * x_1 + 0.5)$, 当$x_1$为0时，结果为1，当$x_1$为1时，结果为0

可以发现，感知机只能解决线性可分问题，不能解决非线性可分的问题。因此要解决非线性可分的问题时，就需要考虑使用多层功能神经元。

3. 多层前馈神经网络

​ 常见的多层神经网络结构如下图所示：

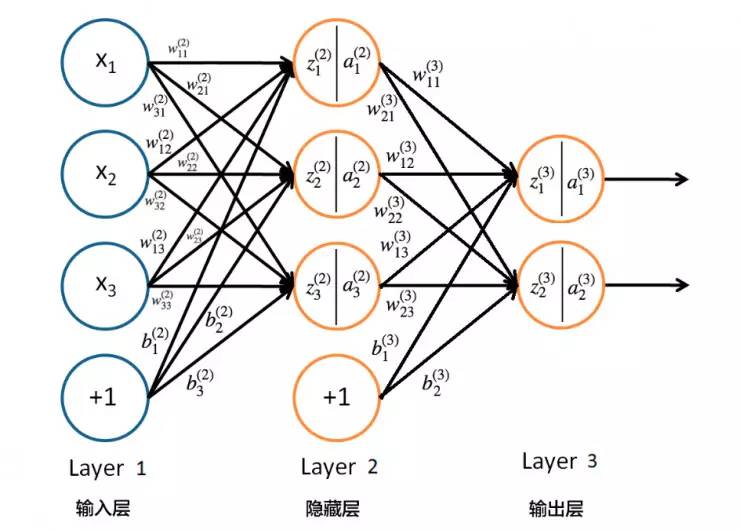
​ 这种层级结构中，每层的神经元与下一层神经元完全互联，但是同层不存在连接，也不存在跨层连接。这样的神经网络结构通常称为“多层前馈神经网络”。所谓前馈是指网络拓扑结构中不存在回路或环路，而不是指信号不能向后传。

​ 这里有三层，依次为输入层、隐藏层和输出层，因此“多层前馈神经网络”也被称为单隐层网络。

​ 接下来的内容，我将主要就周志华老师的《机器学习》中关于神经网络部分的一些公式进行推导与说明。在此向周老师致以敬意。

下面的公式推导与说明都基于上图：

符号说明：

$y_j,b_h,x_i$:分别表示输出层、隐藏层和输入层神经元

$v_{ih}$:表示输入层到隐藏层的权值

$w_{hj}$:表示隐藏层到输出层的权值

$\theta_j$:表示第j个输出层神经元的阈值

$\gamma_h$:表示隐藏层第h个神经元的阈值

假设隐藏层和输出层神经元使用的激活函数为：Sigmoid函数

3.1 神经网络的前向传播

从输入层到隐藏层：

第h个隐藏层神经元的输入：

$$\alpha_h = \sum_{i=1}^{d}v_{ih}x_i$$
第h个隐藏层神经元的 输出：
$$b_h = f(\alpha_h - \gamma_h)$$

$$f(x) = \frac{1}{1+e^{-x}}$$

从隐藏层到输出层：

第j个输出层神经元的输入：

$$\beta_j = \sum_{h=1}^{l}w_{hj}bh$$
第j个输出层的神经元的 输出：
$$y_j^* = f(\beta_j - \theta_j)$$

3.2 神经网络的反向传播(Back Propagation, BP)

​ 在完成前向传播之后，我们可以计算网络在训练样例$(x_k,y_k)$下的均方误差如下：

$$E_k = \frac{1}{2}\sum_{j=1}^{l}(y_j^* - y_j)^2$$
在这个网络中，我们需要确定的参数有 $d*q$个输入层到隐藏层的权值， $q*l$个隐藏层到输出层的权值，q个隐藏层的阈值、l个输出层的阈值共计 $(d+q+l)q+l$个参数，在每一轮迭代中，任意的参数v都可以采用以下的更新估计式：
$$v = v + \Delta v = v - \eta\frac{\partial E_k}{\partial v}$$

其中，$\eta$是学习率。

​ 我们需要优化的权值主要有输入层到隐藏层的权值$v_{ih}$，隐藏层到输出层的权值$w_{hj}$，隐藏层的阈值$\gamma_h$和输出层的阈值$\theta_j$共四类。下面依次来进行更新。

3.2.1 对于隐藏层到输出层的权值$w_{hj}$

$$\Delta w_{hj} = -\eta\frac{\partial E_k}{\partial w_{hj}} = -\eta\frac{\partial E_k}{\partial y_j^*}*\frac{\partial y_j^*}{\partial \beta_j}*\frac{\partial \beta_j}{\partial w_{hj}}$$

其中：

$$\frac{\partial \beta_j}{\partial w_{hj}} = b_h$$

$$\frac{\partial y_j^*}{\partial \beta_j} = f'(\beta_j - \theta_j) = f*(1-f) = y_j^* *(1 - y_j^* )$$

$$\frac{\partial E_k}{\partial y_j^*} = y_j^* - y_j$$

所以，

$$\Delta w_{hj} = - \eta *( y_j^* - y_j) * (y_j^* *(1 - y_j^* )) * ( b_h) = \eta y_j^*(1-y_j^*)(y_j - y_j^*)b_h$$
说明：在做每一个微分时，只关注是对谁进行微分，就可以清晰的得到结果。而我们的f使用的sigmoid函数，sigmoid函数的一阶导数的结果就是 $f'(x) = f(x)(1-f(x))$。

3.2.2 对于输出层的阈值$\theta_j$共四类

$$\Delta \theta_j = -\eta\frac{\partial E_k}{\partial \theta_j} = -\eta\frac{\partial E_k}{\partial y_j^*}*\frac{\partial y_j^*}{\partial \theta_j}$$

其中：

$$\frac{\partial y_j^*}{\partial \theta_j} = f'(\beta_j - \theta_j) = -f*(1-f)（注意负号）$$

$$\frac{\partial E_k}{\partial y_j^*} = y_j^* - y_j$$

所以：

$$\Delta \theta_j =- \eta *( y_j^* - y_j) * (y_j^* *(1 - y_j^* )) = -\eta y_j^*(1-y_j^*)(y_j - y_j^*)$$

3.2.3 对于输入层到隐藏层的权值$v_{ih}$

​ 这个式子很长，为了方便大家看出微分是怎么残生的，我将相关表达式先写出来：

$E_k = \frac{1}{2}\sum_{j=1}^{l}(y_j^* - y_j)^2$ | $y_j^* = f(\beta_j - \theta_j)$ | $\beta_j = \sum_{h=1}^{l}w_{hj}bh$ | $b_h = f(\alpha_h - \gamma_h)$ | $\alpha_h = \sum_{i=1}^{d}v_{ih}x_i$

则更新部分的表达式可写成如下：

$$\Delta v_{ih} = -\eta\frac{\partial E_k}{\partial v_{ih}} = -\eta\frac{\partial E_k}{\partial y_j^*}*\frac{\partial y_j^*}{\partial \beta_j}*\sum_{j=1}^{l}\frac{\partial \beta_j}{\partial b_h} * \frac{\partial b_h}{\partial \alpha_h}*\frac{\partial \alpha_h}{\partial v_{ih}}$$
不难看出，为了更新从输入层到隐藏层的权重，几乎使用了全部的前向传播的公式，其中：
$$\frac{\partial E_k}{\partial y_j^*} = y_j^* - y_j$$

$$\frac{\partial y_j^*}{\partial \beta_j} = f'(\beta_j - \theta_j) = f*(1-f) = y_j^* *(1 - y_j^* )$$

$$\frac{\partial \beta_j}{\partial b_h} = w_{hj}$$

$$\frac{\partial b_h}{\partial \alpha_h} = f'(\alpha_h - \gamma_h) = b_h * (1 - b_h)$$

$$\frac{\partial \alpha_h}{\partial v_{ih}} = x_i$$

于是，最后的表达式可以写为：

$$\Delta v_{ih} = -\eta\frac{\partial E_k}{\partial v_{ih}} =-\eta( y_j^* - y_j)( y_j^* *(1 - y_j^* ))(\sum_{j=1}^{l}w_{hj}*b_h * (1 - b_h)* x_i)$$
整理为：
$$\Delta v_{ih} = -\eta\frac{\partial E_k}{\partial v_{ih}} =\eta y_j^*( y_j - y_j^* ) (1 - y_j^* )b_h (1 - b_h)x_i(\sum_{j=1}^{l}w_{hj})$$

3.2.4 对于隐藏层的阈值$\gamma_h$

$$\Delta \gamma_h = -\eta\frac{\partial E_k}{\partial \gamma_h} = -\eta\frac{\partial E_k}{\partial y_j^*}*\frac{\partial y_j^*}{\partial \beta_j}*\sum_{j=1}^{l}\frac{\partial \beta_j}{\partial b_h} * \frac{\partial b_h}{\partial \gamma_h}$$

这个式子中与上面求对于输入层到隐藏层的权值$v_{ih}$的部分偏微分相同，这里就不重写了。整理后我们可以看出，仅仅比上式少了一个$x_i$，其余部分一样：

$$\Delta \gamma_h = -\eta\frac{\partial E_k}{\partial \gamma_h} =-\eta y_j^*( y_j - y_j^* ) (1 - y_j^* )b_h (1 - b_h)(\sum_{j=1}^{l}w_{hj})$$
这里有个符号的原因与求 $\theta_j$时一样，因为在做减法，那么在进行求导运算的时候，就会产生一个符号。

大家可能也注意到了，这四个式子中都出现了$( y_j^* - y_j)( y_j^* *(1 - y_j^* ))$，我们把这个式子定义为：

$$g_j = ( y_j^* - y_j)( y_j^* *(1 - y_j^* ))$$
那么上面的四组方程就可以简写为：

$$\Delta w_{hj} = \eta g_jb_h$$

$$\Delta \theta_j = -\eta g_j$$

$$\Delta v_{ih} = \eta g_jb_h (1 - b_h)x_i(\sum_{j=1}^{l}w_{hj})$$

$$\Delta \gamma_h = -\eta g_j b_h (1 - b_h)(\sum_{j=1}^{l}w_{hj})$$

4. 最后

​ 以上就是BP算法的公式推导，是建立在每一个训练样例进行一次前向传播之后，立刻进行一次反向传播。这种方式我们叫做“标准BP算法”，但是我们BP算法的目标是要最小化训练集D上的累积误差：

$$E = \frac{1}{m}\sum_{k=1}^{m}E_k$$
即所有的训练样例都遍历了一遍，再执行BP算法，这种算法我们称为 “累积BP算法”