拓扑排序

基本概念：

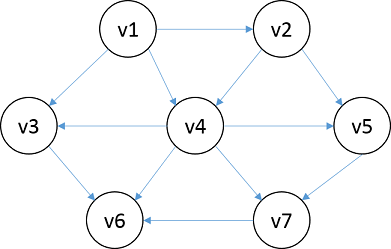
      拓扑排序是对有向无圈图的顶点的一种排序，若一条路径是从vi到vj，那么在排序序列中vj出现在vi后面。显然，如果图含有圈，那么拓扑排序是不可能的，比如对于圈上的两个顶点v和w，v在w之前同时w又在v之前，在排序中是矛盾的。另外，拓扑排序不是唯一的，比如下面一张图的拓扑排序可以是v1,v2,v5,v4,v3,v7,v6或者v1,v2,v5,v4,v7,v3,v6。

算法设计：

1.简单的拓扑排序

      基本思路：找出任意一个没有入边的顶点，然后显示该顶点，并将它和它的边从图中一起删除。然后对图的其余部分应用同样的方法。

      具体细节实现：

      ①把顶点v的入度定义为边（u,v）的条数。

      ②计算图中所有顶点的入度，保存在数组Indegree中。

      ③图被读入一个邻接表中。

      下面是代码实现，测试数据是上图中的顶点：

#include <iostream>
#include <vector>
#include <cstdlib>

using namespace std;

const int MaxSize = 20;

struct ArcNode{
	int adjvex;
	ArcNode* next;
};

//头单元数组
template<class Type>
struct VertexNode{
	Type vertex;
	ArcNode* firstedge;
};

template<class Type>
class Graph{
private:
	VertexNode<Type> adjlist[MaxSize];
	int vertexNum, arcNum;
	Type vertex[MaxSize];
	int Indegree[MaxSize];
public:
	Graph(){
		Type v;
		int i, j;
		vertexNum = 0;
		arcNum = 0;
		cout << "please input the nodes:" << endl;
		while (cin >> v){
			adjlist[vertexNum].vertex = v;
			adjlist[vertexNum].firstedge = NULL;
			vertex[vertexNum] = v;
			Indegree[vertexNum] = 0;
			vertexNum++;
		}
		cin.clear();
		cout << "please input the edges:" << endl;
		Type a, b;
		while (cin >> a >> b){
			findNode(a, b, i, j);
			Indegree[j]++;//计算各顶点的入度
			ArcNode* s = new ArcNode;
			s->adjvex = j;
			s->next = adjlist[i].firstedge;
			adjlist[i].firstedge = s;
			arcNum++;
		}
		cin.clear();
	}

	void findNode(Type a, Type b, int& i, int& j){
		for (int k = 0; k < vertexNum; k++){
			if (vertex[k] == a)
				i = k;
			if (vertex[k] == b)
				j = k;
		}
	}

	void TopSort(){
		int counter;
		Type V, W;
		int Index;
		for (counter = 0; counter < vertexNum; counter++){
			Index = FindNewVertexOfIndegreeZero();
			if (Index == -1){
				cout << "Graph has a cycle!" << endl;
				exit(1);
			}
			cout << vertex[Index] << " "<<flush;
			for (ArcNode* p = adjlist[Index].firstedge; p != NULL; p = p->next){
				Indegree[p->adjvex]--;
			}
		}
	}

	int FindNewVertexOfIndegreeZero(){
		for (int i = 0; i < vertexNum; i++){
			if (Indegree[i] == 0){
				Indegree[i] = -1;//取出该顶点，下次不再考虑
				return i;
			}	
		}
		return -1;
	}
};

int main(){
	Graph<char> g;
	g.TopSort();
	cout << endl;
	return 0;
}

       效率分析：函数FindNewVertexOfIndegreeZero扫描Indegree数组，寻找一个尚未被分配拓扑编号的入度是0的顶点。如果返回-1则表示这样的顶点不存在，也就意味着该图有圈。因为FindNewVertexOfIndegreeZero函数是对Indegree数组的简单顺序扫描，若以每次要花费O（|V|）的时间。由于有|V|次的这样的调用，所以该算法的运行时间为O（V^2）。

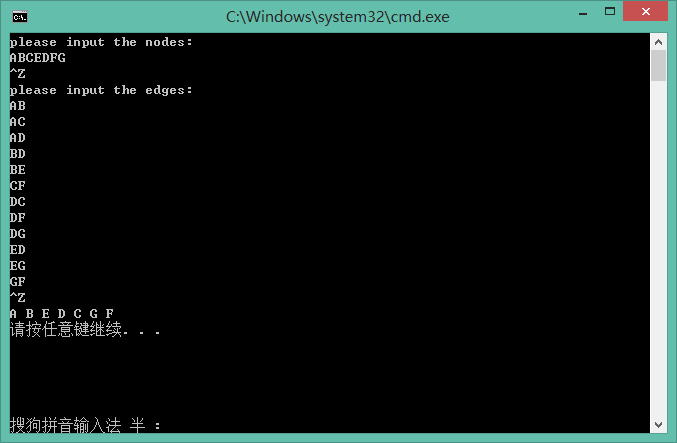
      测试结果：

2.改进的拓扑排序

       上述算法运行时间长的原因在于对Indegree数组的顺序扫描。如果图是稀疏的，那么在每次迭代期间只有一些顶点的入度被更新，但是，尽管只有一小部分发生了变化，但是在搜索入度为0的顶点时潜在地查看了所有的顶点。

      解决方法：使用一个队列，首先，对每一个顶点计算入度，将所有入度为0的顶点放入一个空的队列中。当队列不空时，删除一个顶点v，并将和v邻接的顶点的入度减1，只要有一个顶点的入度降为0，就把该顶点放入队列中。此时，拓扑排序就是顶点出队的顺序。

      下面是代码实现，测试数据 同上：

#include <iostream>
#include <queue>
#include <cstdlib>

using namespace std;

const int MaxSize = 20;
struct ArcNode
{
	int adjvex;
	ArcNode* next;
};

template<class Type>
struct VertexNode{
	Type vertex;
	ArcNode* firstedge;
};

template<class Type>
class Graph{
private:
	VertexNode<Type> adjlist[MaxSize];
	int vertexNum, arcNum;
	Type vertex[MaxSize];
	int Indegree[MaxSize];
public:
	Graph(){
		Type v;
		int i, j;
		vertexNum = 0;
		arcNum = 0;
		cout << "please input the nodes:" << endl;
		while (cin >> v){
			adjlist[vertexNum].vertex = v;
			adjlist[vertexNum].firstedge = NULL;
			vertex[vertexNum] = v;
			Indegree[vertexNum] = 0;
			vertexNum++;
		}
		cin.clear();
		cout << "please input the edges:" << endl;
		Type a, b;
		while (cin >> a >> b){
			findNode(a, b, i, j);
			Indegree[j]++;//计算各顶点的入度
			ArcNode* s = new ArcNode;
			s->adjvex = j;
			s->next = adjlist[i].firstedge;
			adjlist[i].firstedge = s;
			arcNum++;
		}
		cin.clear();
	}

	void findNode(Type a, Type b, int& i, int& j){
		for (int k = 0; k < vertexNum; k++){
			if (vertex[k] == a)
				i = k;
			if (vertex[k] == b)
				j = k;
		}
	}

	int findNode(Type a){
		for (int k = 0; k < vertexNum; k++){
			if (vertex[k] == a)
				return k;
		}
	}

	void TopSort(){
		queue<Type> q;
		int count = 0;
		int Index;
		int i;
		for (i = 0; i < vertexNum; i++){
			if (Indegree[i] == 0)
				q.push(vertex[i]);
		}
		while (!q.empty()){
			Type v = q.front();
			cout << v << " " << flush;
			q.pop();
			count++;
			Index = findNode(v);
			for (ArcNode* p = adjlist[Index].firstedge; p != NULL; p = p->next){
				if (--Indegree[p->adjvex]==0){
					q.push(vertex[p->adjvex]);
				}
			}
		}
		if (count != vertexNum){
			cout << "Graph has a cycle!" << endl;
			exit(1);
		}
	}
};

int main(){
	Graph<char> g;
	g.TopSort();
	cout << endl;
	return 0;
}

      效率分析：如果使用邻接表，这个算法的运行时间为O（|E|+|V|），因为for循环对每条边最多执行一次，队列操作对每个顶点也是最多进行一次。

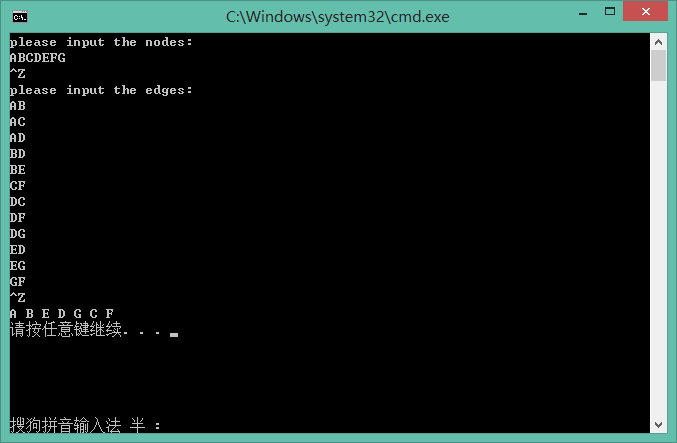
      测试结果：

      

      ps:整理自《数据结构与算法分析——C语言描述》