最小生成树（poj1797）路径最小值最大

                                                           路径最小值最大

kruskal 算法是基于贪心。--最小平均树

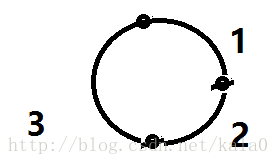
        怎么个贪心：    首先生成树不能有环，那我们给最小生成树添加一条边（随机）使得其变成环，模拟初步的图的环境，观察有什么规律可以得到。

        

        假如之前是1 2 我们添加3，那么可以删除 3.

        假如之前是1 3 我们添加2，那么可以删除 3.

        假如之前是2 3 我们添加1，那么可以删除 3.

删除环中最大的那个。那么我们的最小生成树还在。

应该有人会想，这个删除操作影响其余的树结构吗？？

        答案：不会。

这样我们先将权值小的(排序)让其生成最小生成树，反正权值最大会被删（在某环内）。

而且只需要生成到n-1边就结束了。