1. B树基本概念
1.1 B树背景
B树是用于在外存工作的平衡搜索树。
当数据比较大,无法全部存入内存时,需要将部分数据存在外存中,在需要的时候读入内存,修改之后又写回外存。由于外存的速度与内存有几个数量级的差别,所以节省在外存上花的时间,对搜索树的性能提高时最有效的。
最常见的外存就是磁盘。磁盘是快设备,也就是说磁盘的读写单位是以块为单位,一般地块大小从0.5k到4k。即使你只读取一个字节,磁盘也是将包含该字节的所有数据读取到硬盘中。而在磁盘读取过程中,最占用时间的是磁盘的寻道,也就是磁头在盘片上找到需要读取的块所在位置的时间,而在盘片上顺序读取数据的所花的时间是占比比较小的。
要减少外存上花的时间,就可以从减少读盘次数以及减少寻道时间着手。
B树采取的方法就是,就充分的利用盘块的空间,在一个盘块中尽可能多的存储信息,或者在连续的盘块地址上存储尽可能多的信息。在数据结构上的变化就是每个节点存储多个key信息以及包含多个子节点。增加节点的分支树,就可以使得这棵树的高度降低,比如高度为2(roo高度为0)分支1000的数,就以存储1000*1000个关键字信息,而二叉树j的高度就至少需要6*ln10。
如下图,M,D,J等称为key,也就是存入B树种的数据项。
图1 -B树示例(来自《算法导论》)
1.2 B树定义
(来自《算法导论》第三版)
B树T有如下性质:
1. 每个节点x有如下属性:
-
-
- x.n表示节点当前key的个数。
- x中key满足:x.key1 <= x.key2<= x.key3 <= .... <= x.keyx,n。也就是x中的key以非降序顺序排列。
- x要么是叶子节点,要么是内部节点。
-
2. 每个内部节点包含x.n + 1 个引用,指向x.n + 1个孩子节点。叶子节点没有孩子节点。
3. x的key将孩子节点区分开,也就是满足:设ki 为 子树i中的任意key值,k
1 <= x.k
1 <= k
2 <= x.k
2 ....<= x.k
x.n <= k
x.n+1.
4. 所有的叶子节点在同一层
5. 每个节点拥有的key以及孩子的数量有约束,设整数 t>=2 为最小度:
-
-
- 除根节点外,每个节点必须有至少t-1个key,t个孩子。树不为空时,根节点至少有一个key。
- 每个节点至多有2*t-1个key,每个内部节点至多有2*t个孩子。当一个节点有2*t-1个key时,称其为满节点。
-
t=2的B树称为2-3-4树,因为可以由2-3-4个孩子。
2. B树基本操作
2.1 查找
B树的查找和二叉树查找类似,首先在当前节点中查找,如果没有并且存在孩子节点,就递归的到可能存在该key的孩子节点中查找。
不同的是,B树节点有多个key,需要每个都比较,为了提高性能,可以使用二分法加速节点中的查找。

图2 -B树查找伪码(来自《算法导论》)
2.2 树的创建
B树创建很简单,将B树节点分配为一个空的叶子节点即可。
2.3 插入key
B树的插入只会在叶子节点中插入key,内部节点之后将插入操作传递到适当的子树中去,知道叶子节点中。
B树的插入需要考虑的一个问题就是当节点以满时,需要将该节点分裂成两个节点。
一个满的节点有2*t-1个key,内部节点有2*t 个孩子,分裂将其分成两个各有t-1个key,内部节点各t个孩子,多余的一个节点插入到父节点中,作为分裂之后两个节点的分割key。
如图,一个最小度为3的满节点,分裂之后,key C上移到父节点,成为分裂之后两个节点的分割key。分裂之后,父节点多了一个key和一个孩子。
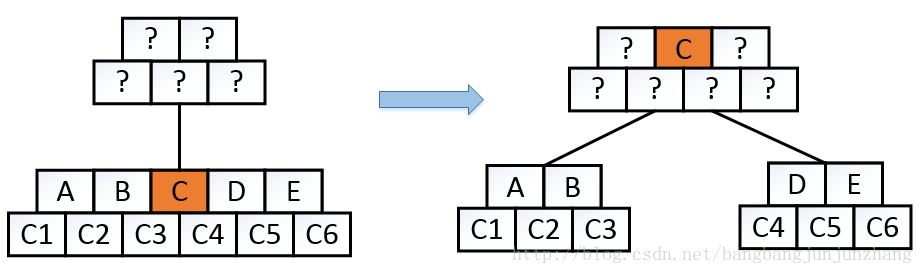
图3 -B树分裂示例
为了是插入操作可以顺树根到叶子节点一遍完成,而不需要回溯到父节点中,需要做如下操作:
-
- 若是根节点,则生成一个新的根节点,原根节点作为新根节点的第一个孩子,并对该孩子进行分裂操作。
- 若是内部节点,每次向适当孩子传递操作时,都需要检查该子树是否已满,若满则进行该子树,再将插入操作传递到适当的子树中。
- 若是叶子节点,则在适当的位置插入需要插入的key
如此,则传递到需要操作的叶子节点都是不满的,都可以直接进行插入操作。并且可以看到,B树的高度增加只有在根节点已满时,分裂根节点增加高度,所以使得所有叶子节点的高度一样。
插入示例:
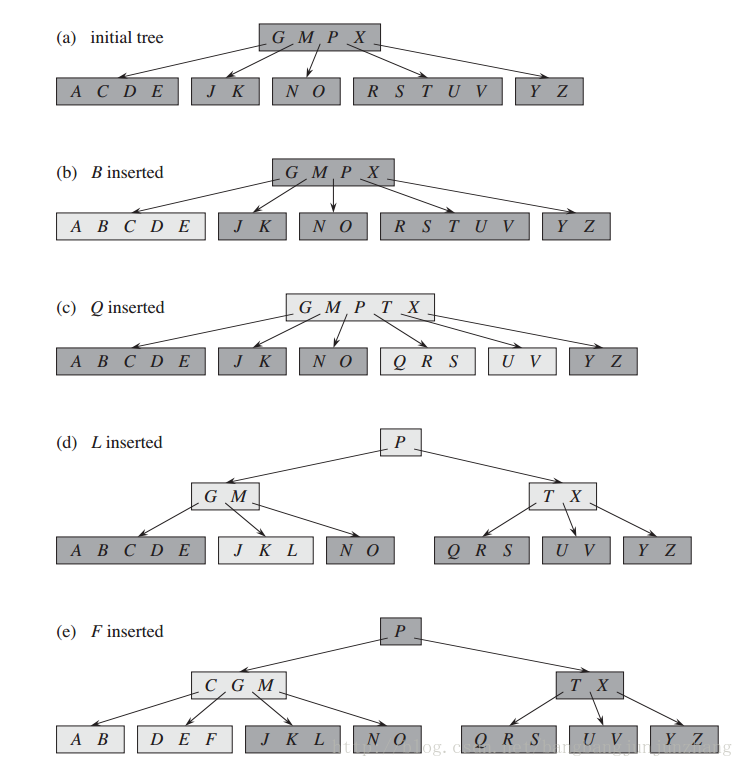
图4 -B树插入示例(来自《算法导论》)
该B树最下度为3,所以节点最多有5个key,最少有2个key。
- b) 插入B:孩子未满,直接插入
- c) 插入Q:孩子已满,分裂子树,key T上移到父节点中,然后在将Q插入到适当的孩子中
- d) 插入L:root已满,生成新root节点,分裂老root节点,在适当子树中插入适当孩子中
- e) 插入F:孩子已满,分裂子树,key C上移到父节点,在适当节点中插入Q
2.4 删除key
删除的时候,当key存在的节点的key数量等于t-1时,再删除就会破坏B树属性,所以为了不回溯,在删除操作传递到子树中之前,需要检查子树key的数量。
删除操作步骤如下:
- 待删除key如果在当前节点中,转2,否则转8
- 当前节点是叶子,直接删除,完成删除操作。否则转3
- 待删除key分割的子树中,前一棵子树key的数量大于t-1,转4,否则转5.
- 从前一颗子树中删除该子树根节点中最大的key,将该key替换当前节点中待删除key,完成删除操作。
- 待删除key分割的子树中,后一棵子树的key数量打于t-1,转6,否则转7.
- 从后一颗子树中的根结点中删除该节点最小的key,用该key替换待删除key,完成删除。
- 合并该节点分割的两个子树,并从合并之后的子树中删除待删除key。
- 找到key可能存在的子树Tn,转9
- 该子树前一颗子树Tn-1的根节点key数量大于t-1,转10,否则转12
- 将Tn-1中最大的key替换当前节点中适当的key,并将被替换的key插入到Tn中,转11
- 将Tn-1中最后一个孩子,移动到Tn中适当的位置,将删除操作传递到Tn中。
- Tn的后一颗子树Tn+1的根节点key数量大于t-1,转13,否则转?
- 将Tn+1中最小的key替换当前节点,并将被替换的key插入到Tn+1中,转14
- 将Tn+1中最小的子树移动到Tn中,将删除操作传递Tn中。
删除中,可能会出现根节点没有key的情况,所以删除结束之后需要检查根节点,若发生这种情况,需要将根节点更新为原根节点的唯一的一颗子树。
示例:
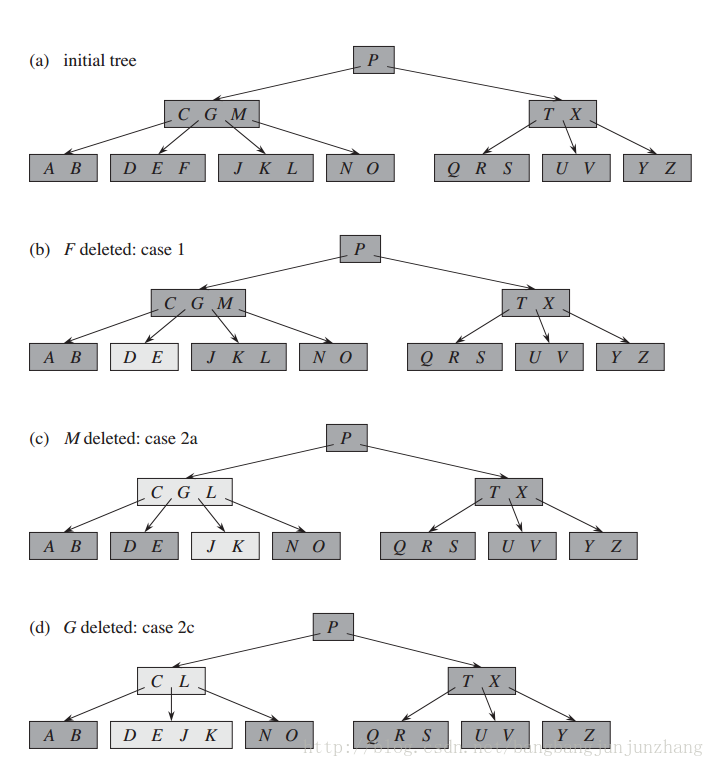









 本文介绍了B树的基本概念,包括其背景和定义,并详细阐述了B树的查找、创建、插入和删除操作。通过代码实现,展示了如何在Java中构建B树结构,包括AbstractBTreeNode、BTreeInternalNode、BTreeLeaf和BTree类的设计与应用。
本文介绍了B树的基本概念,包括其背景和定义,并详细阐述了B树的查找、创建、插入和删除操作。通过代码实现,展示了如何在Java中构建B树结构,包括AbstractBTreeNode、BTreeInternalNode、BTreeLeaf和BTree类的设计与应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 3581
3581

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








