问题 A: 约数个数
题目描述
p^ q 表示p的q次方，正整数M可以分解为M=(p1 ^ a1 )(p2 ^ a2)(p3 ^ a3)……(pn ^ an)的形式，其中p1，p2……pn为质数(大于1并且只能被1和自身整除的数叫做质数)。a1，a2……an为整数。例如18=(2 ^ 1) (3 ^ 2)，45=(3 ^ 2)(5 ^ 1)。
给出n和一个质数g，以及正整数M分解后的形式，求M的所有约数中，有多少能被g整除。
输入
第一行 两个数 n和g。 0<n<=10 1<g<100。g为质数。
第二行 n个数 p1到pn 1<pi<100 pi为质数（1<=i<=n）。
第三行 n个数 a1到an 0<=ai<=20 ai为整数（1<=i<=n）。
保证对于任意的i,j(i != j) ,pi != pj
输出
一个数
表示M的所有约数中，有多少能被g整除。
样例输入
2 3
3 5
2 2
样例输出
6
提示
样例解释：
M=(3 ^ 2)(5 ^ 2)=925=225
225能被3整除的约数有3 9 15 45 75 225 共6个。
坑点：没用long long导致结果溢出
思路：把所有pi和ai各用一个数组盛起来，并在pi里找到与g相等的一项，特殊标记（假设该项为pm）。
最后结果为(a1+1) * (a2+1) * (a3+1) * … * (am) *…(ai+1)
注释1:ax+1表示px的次数可为0到ax。
注释2:am处不用+1因为g^0时的数字不是g的倍数。
#include <stdio.h>
#define INITNUM -1
int main(){
//mark:与g相等的pi的下标，初值为INITNUM
int n,g,mark=INITNUM;
//sum:总约数的个数
//注意，不用longlong会溢出
long long sum=1;
int a[11],p[11];
scanf("%d%d",&n,&g);
for(int i=0;i<n;i++){
scanf("%d",&p[i]);
//载入 p的同时寻找与g相等的项并记录下标
if(p[i]==g&&p[i]!=0) mark=i;
}
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
//下标等于初值时表明g不在p中，无解
if(mark==INITNUM){
puts("0");
return 0;
}
for(int i=0;i<n;i++){
//pi不等于g，则总约数*=(ai+1), 因为可能存在pi^0的情况
if(i!=mark){
sum*=(a[i]+1);
}
//pi等于g，则总约数*=ai，此处不用ai+1因为g^0时的数字不是g的倍数 （前提：本题强调pi不重复）
else{
sum*=(a[i]);
}
}
printf("%ld",sum);
return 0;
}
问题 B: Alice and Bob
题目描述
Alice and Bob decide to play a game. At the beginning of the game they put n piles of sweets on the table.The number of each pile of sweets may be different. Alice and Bob take away sweets in turn,and always Alice takes sweets first in every games.Each time in their turn they can get only one whole pile of sweets.When there is no sweet left, the game is over. Finally, The man who have the largest number of sweets in hand will win.
Assume that Alice and Bob were very clever.
输入
The first line is an integer n, which means that there are n pile sweets.
1 <= n <= 100000
Next n integers, the i-th integer means the number of sweets in the i-th pile.
The number of sweets in each pile is less than 10000.
输出
If Alice wins, output “A”, and if Bob wins, output “B”.
Otherwise output “again”
样例输入
样例输入1:
3
1 6 7
样例输入2:
4
3 3 3 3
样例输出
样例输出1:
A
样例输出2:
again
坑点：冒泡排序法超时。
卡壳原因：比赛的时候不记得快速排序的qsort函数参数是那几个了。
思路：将所有糖果堆的数量存入数组，而后降序排序。之后模拟Alice和Bob轮流拿取糖果的过程。
#include <stdio.h>
#include <stdlib.h>
int cmp(const void*a,const void*b){
return *(int*)b-*(int*)a;
}
int main(){
//turn:当前操作者的标记，1代表alice，0代表bob
int t,suma=0,sumb=0,turn=1,n,a[100002];
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
}
//快速排序法生成降序序列
qsort(a,n,sizeof(int),cmp);
for(int i=0;i<n;i++){
if(turn) {
suma+=a[i];
turn=0;
}
else{
sumb+=a[i];
turn=1;
}
}
if(suma>sumb) puts("A");
else if(suma<sumb) puts("B");
else puts("again");
return 0;
}
问题 F: 折纸达人
题目描述
小明最近对折纸很感兴趣，他想知道一张正方形的纸在多次折叠以后沿纸的中线用剪刀将其剪开能得到多少张纸？
输入
第一行一个整数t,表示一共有t组数据(1 <= t <= 100)
每组输入数据包括三行
第一行为一个整数n，表示有n次操作(1 <= n <= 10^5)
第二行为n个大写字母(四种情况L,R,T,B L表示从左向右折 R表示从右向左折 T表示从上向下折 B表示从下向上折)
第三行为两个字母(四种情况 LR,RL,TB,BT LR表示从左向右剪 RL表示从右向左剪 TB表示从上往下剪 BT表示从下往上剪)
输出
输出一个整数表示能得到的纸的数目
答案可能过大 需要对1000000007 (1e9+7)取模
样例输入
2
2
BB
LR
1
R
LR
样例输出
5
2
卡壳原因：不会对1e9+7这类数字的取模技巧，导致结果过大时总是溢出
思路请见：苗学姐的题解
我的思考过程：左右剪切只与对上下对折的次数有关，上下剪切只与对左右对折的次数有关。因为折叠一次使纸的层数增加一倍，而此时只有平行于折痕方向裁剪才会使纸片数量增加一倍。(你可能需要找张纸体会体会)同时因为纸片数量接近于指数式增长，所以需要及时取模来防止溢出。
#include <stdio.h>
#define MOD 1000000007
int main(){
long long slr;//左右折叠
long long stb;//上下折叠
int n,t,x;
char cmd[100008];
scanf("%d",&t);
while(t--){
slr=stb=1;//开始时纸片只有一层
scanf("%d",&n);
scanf("%s",cmd);
for(int i=0;i<n;i++){
if(cmd[i]=='L'||cmd[i]=='R'){
slr*=2;
slr%=MOD;//及时取模，防止溢出
}
else if(cmd[i]=='T'||cmd[i]=='B'){
stb*=2;
stb%=MOD;//及时取模，防止溢出
}
}
scanf("%s",cmd);
if(cmd[0]=='L'||cmd[0]=='R'){
stb=stb%MOD;//再模一遍，防止溢出
printf("%d\n",stb+1);//+1是计算上位于纸片中央的那一条，请自行结合实物理解
}
else if(cmd[0]=='T'||cmd[0]=='B'){
slr=slr%MOD;//再模一遍，防止溢出
printf("%d\n",slr+1);
}
}
return 0;
}
问题 H: 神奇老虎机
题目描述
不知道你有没有玩过老虎机，现在小明面前有一台神奇的老虎机，这台机器有n个滚轮，从左往右数第i个滚轮包含1到a_i的整数(包括1和a_i)。在按下按钮之后，所有的滚轮都会飞速旋转，最终停下来，每个滚轮将显示其中一个整数。这个过程是随机的。小明有一个有趣的想法，如果将滚轮显示的数字连接起来看做一长串字符串的话，将会有非常多的可能，在这所有的可能中字典序最小的字符串是哪个？（只能从左向右读）
对于字典序的说明:
两个字符串S和T，从前往后比较，如果存在一个位置，在该位置两个字符串的字符不同，则比较小的那个所在的字符串字典序更小。
例如: 123的字典序比14的小，因为在第二个位置上2小于4
12345的字典序比9的小
220的字典序比22的大，因为22是220的一个前缀
输入
一个整数t，表示有t组数据(1 <= t <= 100)
每组第一行为一个整数n表示老虎机有n个滚轮
(1 <= n <= 1000)
第二行为n个整数（a_1 a_2 … a_i … a_n ）
表示第i个滚轮上的数字范围(1~a_i)
(1 <= a_i <= 100)
输出
每组输入对应一行输出，输出字典序最小时老虎机滚轮上显示的数字
两个数字之间用空格隔开
样例输入
2
4
6 6 6 6
2
2 2
样例输出
1 1 1 1
1 1
提示
老虎机上显示的数都不含前导0
比如：某一块滚轮包含[1,33]，如果它显示"1"的话，显示的是"1"而不是"01"
对于样例2的解释：
所有情况分别为：“1 1”、“1 2”、“2 1”、“2 2”
其中"1 1"是字典序最小的，所以答案为"1 1"
坑点：若要满足条件，最后一个滚轮的最小字典序必为1
思路：除最后一个滚轮外的滚轮的最小字典序为10 ^ n (该数为小于等于ai的10 ^ n所能表示的最大值)
#include <stdio.h>
int main(){
//a:当前滚轮所能显示的最大整数
int n,t,a;
scanf("%d",&t);
while(t--){
scanf("%d",&n);
while(n--){
scanf("%d",&a);
//最后一个滚轮所能生成的最小字典序为1
if(n==0) printf("1");
else{
if(a>=100) printf("100");
else if(a>=10) printf("10");
else printf("1");
printf(" ");
}
}
printf("\n");
}
return 0;
}
问题 L: 寄蒜几盒？
题目描述
现在有一个圆圈，圆圈上有若干个点，请判断能否在若干个点中选择三个点两两相连组成一个等边三角形？
这若干个点在圆圈上按顺时针顺序分布。
如果可以的话输出"Yes"(不含引号)
不可以的话输出"No"(不含引号)
输入
第一行一个整数n，表示圆圈上有n个点
第二行n个整数，分别表示第1个点与第2个点之间圆弧的长度、第2个点与第3个点之间圆弧的长度······第n个点与第1个点之间圆弧的长度
3 <= n <= 10^6
1 <= x_i <= 1000 ( 1 <= i <= n)
输出
如果可以组成等边三角形则输出"Yes"(不含引号)
否则输出"No"(不含引号)
样例输入
样例输入1：
4
1 1 2 2
样例输入2：
8
4 2 4 2 2 6 2 2
样例输出
样例输入1：
Yes
样例输入2：
Yes
提示
对于样例2配图：
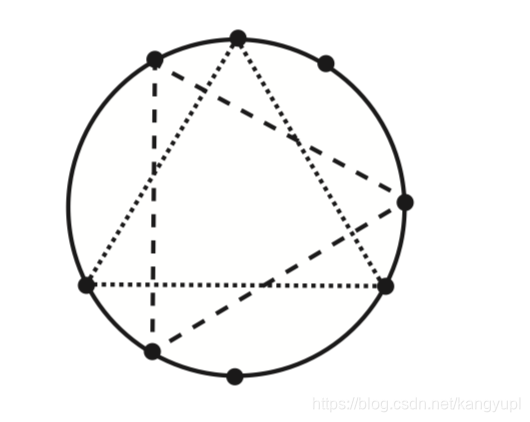
思路：尝试以每一个点为起始点创建两段长度为1/3周长的相邻的圆弧，具体请看代码里的注释
#include <stdio.h>
int main(){
int a[100002];
//sum:圆的周长 len：第一段圆弧的长 len2：第二段圆弧的长
int n,sum=0,len,len2;
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
sum+=a[i];
}
//因为所有圆弧段长度为整数，所以圆周长不能被三整除时一定无解
if(sum%3!=0){
puts("No");
return 0;
}
//遍历所有点，并尝试以当前遍历的点为起始点
for(int i=0;i<n;i++){
len=0;
for(int j=i;;j++){
//下标越界时重置
if(j>=n) j=0;
//计算起始点到当前点的总圆弧长
len+=a[j];
//要存在一个等边三角形，则需要三段长为1/3周长的圆弧
//大于1/3周长，表示以当前起始点无法构建等边三角形，故弃之
if(len>sum/3){
break;
}
//等于1/3周长，则成功找到一段1/3周长的圆弧，开寻找第二段
if(len==sum/3){
//逻辑与找第一段1/3周长圆弧的算法相同
len2=0;
for(int k=j+1;;k++){
if(k>=n) k=0;
len2+=a[k];
if(len2>sum/3){
break;
}
//存在第二段1/3周长的圆弧，则必存在第三段1/3周长的圆弧，输出yes结束
if(len2==sum/3){
puts("Yes");
return 0;
}
}
}
}
}
puts("No");
return 0;
}
扫一扫
2175
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
