Description
给出 N 个正整数
a[1…N] ,再给出 K 个关系符号(>、<或=)s[1…k] 。选出一个长度为 L 的子序列,要求这个子序列的第i 项和第 i+1 项的的大小关系为 s[(i−1)%K+1] 。求出 L 的最大值。Input
- 第一行两个正整数,分别表示
N 和 K(N,K≤5∗105) 。
- 第二行给出 N 个正整数,第i个正整数表示
ai(ai≤106) 。- 第三行给出 K 个空格隔开关系符号(>、<或=),第
i 个表示 si 。Output
- 一个正整数,表示 L 的最大值。
- 第二行
L 个整数,表示一种方案序列(Multiple Answers)。Sample Input
7 3
2 4 3 1 3 5 3
< > =Sample Output
6
2 4 3 3 5 3
Solution :
一开始我是这么想的:对于当前每个值,枚举以它结尾可能的子序列长度,然后再判断前面是否有数能满足。这样的复杂度是 O(N2logN) ,搞笑一般的暴力。
在考虑优化的时候,当前的最优解分别从所有满足
A[j]
(str[Len−1]
(<、>和=)
)
然而实际上并不需要考虑的这么麻烦,定义 dp[i] 表示以 Ai 作为结尾,最长的子序列长度。那么有个玄学的推论:
- 该点的最优解一定是从前面某位置的最优解更新来的(即如果要从 Ai 来更新,则一定是所有以它为末尾元素的合法子序列中最长的那条,也即 dp[i] )。
讲着是推论其实我不太清楚是怎么推的。
(16/10/4晚更新)终于基本搞清楚怎么推了,感谢焱犇神牛的证明。
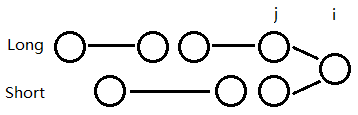
为证明上述命题,我们需证下图所示的命题:
- 对于点
i
可能继承的两条子序列
Long 与 Short ,当 j 所在的子序列位置不是最优解dp[j]=lengthLong 时, dp[i] 不可能达到最优。
此时对于
Long
序列,设
j
出现的位置为
y<x (注意 x−y≥1 )。-
dp[i]=y+1
,且
i
无法从
Long 序列继承。 根据上述条件,我们得到以下推论:
位置 x 与位置
y 的符号不同。
假设其相同。由于两个位置上的值同为 aj ,那么显然 Long 序列是可以代替 Short 序列的, Short 序列不会比继承 Long 序列优。所以 aj 与 ai 一定满足 y 位置上的符号关系,而不满足x 位置上的符号关系。aj 与 ai 一定不相等。
假设其相等。若位置 x 为′=′ ,则一定选Long序列继承;若位置 x 不为′=′ ,由于相等, i 仍然可以从x−1 转移过来,由于 x−1≥y ,所以选 Long 序列不会比 Short 差,不必从 Short 序列继承 y 。位置
y 的符号一定不是 ′=′ 。
因为由上述两推论可以知道,由于一定要从 Short 序列更新,且 aj≠ai ,所以一定不是 ′=′ 。
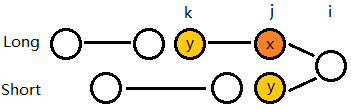
我们可以在 Long 序列中找到位置 y 对应的原序列位置
k 。那么有结论:-
ak
与
ai
不满足位置
y
的符号关系。
显然如果满足了那就不必从Short 序列更新了。
根据上述结论:
- 假设
x
位置是小于或等于号:
y 位置的符号就是大于号(推论1,推论3),所以 ak<ai (推论4)。由于 x 位置无法被i 继承,所以应该有 aj>ai (推论2)。紧接着我们就可以得到ak<ai<aj(k<j<i)又因为 k 位置的符号是大于号,所以必然能找到且 l 位置的符号必然是ak>al<aj(k<l<j) ′<′ 。那么现在, dp[k]=y , dp[l]=y+1 , dp[i]=y+2>y+1 。 - 假设
x
位置是小于或等于号,同理可证依旧有
dp[i]>y+1 。
综上所述,无论 Short 内 y 位置的符号如何,我们总能在
Long 内找到一点,使得 i 可以从该点继承,并且该点可以继承Long 内的 y 位置,保证最优结果一定≥y+2 。这TM能做?
后面就简单多了。
dp[i]=max⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪dp[j]A[j]>A[i],str[dp[j]]=′>′A[j]=A[i],str[dp[j]]=′=′A[j]<A[i],str[dp[j]]=′<′分别采用能够区间查询最值的数据结构维护一下就可以了,下面给出线段树和树状数组(写树状数组的一般都很神奇)的写法。线段树:
#include <bits/stdc++.h> #define M 500005 #define P 1000000 using namespace std; int A[M];char str[M],buf[5]; struct Segment{ int tree[P+5<<2]; void up(int p){tree[p]=max(tree[p<<1],tree[p<<1|1]);} void update(int L,int R,int x,int val,int p){ if(L==R){ tree[p]=max(tree[p],val); return; } int mid=L+R>>1; if(x<=mid)update(L,mid,x,val,p<<1); else update(mid+1,R,x,val,p<<1|1); up(p); } int query(int L,int R,int l,int r,int p){ if(l>r)return 0; if(L==l&&R==r)return tree[p]; int mid=L+R>>1; if(r<=mid)return query(L,mid,l,r,p<<1); else if(l>mid)return query(mid+1,R,l,r,p<<1|1); else return max(query(L,mid,l,mid,p<<1),query(mid+1,R,mid+1,r,p<<1|1)); } }Mx,Mi;//> < int Past[P+5],dp[M]; int main(){ int n,m; scanf("%d %d",&n,&m); for(int i=1;i<=n;i++)scanf("%d",&A[i]); for(int i=1;i<=m;i++){ scanf("%s",buf);str[i]=buf[0]; } int ans=0,tot=0; for(int i=1;i<=n;i++){ dp[i]=dp[Past[A[i]]]+1; dp[i]=max(dp[i],Mx.query(1,P,A[i]+1,P,1)+1); dp[i]=max(dp[i],Mi.query(1,P,1,A[i]-1,1)+1); if(ans<dp[i])ans=dp[i],tot=i; char c=str[(dp[i]-1)%m+1]; if(c=='=')Past[A[i]]=i; else if(c=='>')Mx.update(1,P,A[i],dp[i],1); else Mi.update(1,P,A[i],dp[i],1); } // for(int i=0;i<=n;i++)printf("%d\n",dp[i]); printf("%d\n",ans); stack<int>Ans; int val=ans,hre=A[tot]; Ans.push(hre); for(;tot;--tot) if(dp[tot]+1==val){ char c=str[(dp[tot]-1)%m+1]; if(c=='='&&A[tot]==hre||c=='>'&&A[tot]>hre||c=='<'&&A[tot]<hre){ val--;hre=A[tot];Ans.push(hre); } } while(!Ans.empty())printf("%d%c",Ans.top(),Ans.size()==1?'\n':' '),Ans.pop(); }树状数组:
#include <bits/stdc++.h> #define M 500005 #define P 1000000 using namespace std; int A[M];char str[M],buf[5]; struct Binary_Indexed{ int tree[P+5]; #define lowbit(x) x&(-x) void add_Mi(int pos,int val){ while(pos<=P){ tree[pos]=max(val,tree[pos]); pos+=lowbit(pos); } } int query_Mi(int pos){ int ans=0; while(pos){ ans=max(ans,tree[pos]); pos-=lowbit(pos); } return ans; } void add_Mx(int pos,int val){ while(pos){ tree[pos]=max(val,tree[pos]); pos-=lowbit(pos); } } int query_Mx(int pos){ int ans=0; while(pos<=P){ ans=max(ans,tree[pos]); pos+=lowbit(pos); } return ans; } }Mx,Mi; int Past[P+5],dp[M]; int main(){ int n,m; scanf("%d %d",&n,&m); for(int i=1;i<=n;i++)scanf("%d",&A[i]); for(int i=1;i<=m;i++){ scanf("%s",buf); str[i]=buf[0]; } int ans=0,tot=0; for(int i=1;i<=n;i++){ dp[i]=dp[Past[A[i]]]+1; dp[i]=max(dp[i],Mx.query_Mx(A[i]+1)+1); dp[i]=max(dp[i],Mi.query_Mi(A[i]-1)+1); if(ans<dp[i])ans=dp[i],tot=i; char c=str[(dp[i]-1)%m+1]; if(c=='=')Past[A[i]]=i; else if(c=='>')Mx.add_Mx(A[i],dp[i]); else Mi.add_Mi(A[i],dp[i]); } printf("%d\n",ans); stack<int>Ans; int val=ans,hre=A[tot]; Ans.push(hre); for(;tot;--tot) if(dp[tot]+1==val){ char c=str[(dp[tot]-1)%m+1]; if(c=='='&&A[tot]==hre||c=='>'&&A[tot]>hre||c=='<'&&A[tot]<hre){ val--;hre=A[tot];Ans.push(hre); } } while(!Ans.empty()) printf("%d%c",Ans.top(),Ans.size()==1?'\n':' '),Ans.pop(); }
-
dp[i]=y+1
,且
i
无法从

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








