谱聚类中经常用到的一个图论定理: Number of connected components of the laplacian matrix

Proposition: (Number of connected components of ):     Let  be an undirected graph with non-negative weights. Then the multiplicity  of the eigenvalue 0 of  equals the number of connected components  in the graph. The eigenspace of eigenvalue 0 is spanned by the indicator vectors  of those components.

 

---

下面是个人参考了一篇谱聚类的综述性论文后对这个定理的理解，这个定理可以总结成：当是一个非负权重无向图的拉普拉斯矩阵时，其特征值的个数等于无向图中成分的个数，也就是图最终被切割后的部分。我自己的理解分成两部分：

一、拿无向图切割后的单个部分讲解，也就是上面提到的components中的一个，，是图内点之间的权重矩阵，是点的个数， 是他的拉普拉斯矩阵，是拉普拉斯矩阵特征值对应的特征向量。那么可以列出下面这个式子：

• 由于是处于切割后同一个component的点，所以两点间的权重，所以，特征值对应的特征向量的值都是一样的，也就是说这个component里面每个点都有一个相同的标记值，又因为特征值是，所以对应的特征向量可以缩减为全为的向量即，，这个向量就是论文里经常看到的 indicator vector。这是我想说的第一点：特征值可以让权重不为，也就是点之间有连接的点呈现相同的 indicator value：；
• 还有一个点可以帮助后面的理解：拉普拉斯矩阵不止有一个特征值，但是其他的非零特征值没有这个作用，相同一个component里的会呈现不同的值，无法判定是否是同一个component的。所以是其中一个特殊的特征值。切割后单个component的特征值，可以给这个component里的所有点赋予一个相同的indicator value：。

二、现在考虑多个components的情况，这里涉及到关于谱聚类的一个标准：输入是块对角的矩阵可以保证谱聚类结果的准确性。当时不知道这个是啥意思，现在我觉得可以这么理解，当很多个components的拉普拉斯矩阵可以组成下面的块对角形式时：

这应该只是一个矩阵分析上的定理，当  是各个components的拉普拉斯矩阵  在对角线上组成时，其特征值和特征向量是由各个components的特征向量和特征值组成，我下面用matlab的一个例子说明：

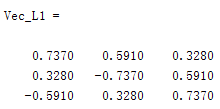
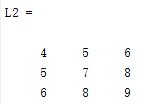
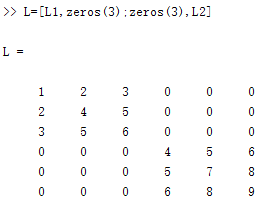
可以看到的特征值/向量来源于各个components的拉普拉斯矩阵的特征值/向量。所以为什么要保证输入是有精确块对角结构的矩阵，就是希望不要各个components之间互相干扰。那么不干扰的话有什么好处？

各个components的特征值及其对应的特征向量不会被干扰，而每个特征值对应的特征向量可以标志他们是相同类别的，也就是说每个特征值对应同一类，所以才有了这个拉普拉斯矩阵特征值个数等于类别个数的结论。我觉得这也是谱聚类最后做完特征值分解只取数目与类别个数相等的特征向量的缘故了。

比如做聚类的时候，就可以通过对拉普拉斯矩阵的特征值个数进行数学约束，使得由数据样本构造的图被分成对应的components数目。当然，通过这个底层的东西，可以构造出其他的一些“范数”，只要最终是对拉普拉斯矩阵的特征值或者说奇异值进行操作就可以，个人是这么认为的，我觉得可能也是一些论文的范数看上去很新，但是最终都是围绕在奇异值或者特征值上的计算，当然，这只是个人看法，也可能有误，只能以后通过更多的文献来对现在的这个想法做更正，现在只是为了做个笔记。

---

最后再做个小结：

拉普拉斯矩阵特征值个数等于无向图中子图的块数，这个结论原因有2：

1. 每个component得到的拉普拉斯矩阵众多特征值中只有特征值可以使得相同components在特征向量上呈现相同的值，也就是说一个component对应一个0特征值及其 特征向量作为标志；
2. 众多components组合得到的块对角拉普拉斯矩阵的特征值和特征向量由各个components的特征值和特征向量组合而成

所以可以直接通过0特征值推导最后分成的components的块数。